Лекция 1.
Тема лекции: Дифференциальное исчисление функции одной
переменной.
Оглавление:
1. Производная функции.
2. Правила и формулы дифференцирования.
3. Логарифмическое дифференцирование.
4. Дифференцирование неявных функций.
5. Дифференциал функции.
6. Дифференцирование функций, заданных параметрически.
7. Производные и дифференциалы высших порядков.
8. Применение производной к вычислению пределов.
Цели лекции: Дать понятие производной и дифференциала функции и способы их вычисления.
После изучения рассматриваемого материала Вы сможете вычислять производные функций и ее дифференциалы, применять производную при вычислении пределов.
Информационные источники.
1.Пискунов Н.С. Дифференциальное и интегральное исчисления.
Т. 1,2. М.; Наука (любое издание).
2. Лычкин В.Н.Высшая математика. Учебное пособие. РГАЗУ, 2011.
3. Лычкин В.Н.Высшая математика в задачах. Учебное пособие. РГАЗУ, 2009.
1. Производная функции.
Пусть
функция
непрерывна на интервале (a;
b).
Придадим
аргументу х приращение ∆х, которое вызовет приращение функции
(здесь х
и х+∆х
принадлежат интервалу (a;
b).
Определение. Производной функции в точке х называется
предел отношения приращения функции ∆у к вызвавшему его прираще-
нию аргумента ∆х, когда последнее стремится к нулю.
Для обозначения
производной функции
используют следующие символы: у′
или
( по Лагранжу),
или
(по Лейбницу).
С учетом принятых обозначений имеем:
. (1)
Процесс нахождения производной функции называется ее дифферен-
цированием.
Если функция имеет производную в каждой точке интервала (а; b), то эту функцию называют дифференцируемой на этом ин-
тервале.
Пусть функциональная зависимость s = s(t) есть закон прямолиней-
ного движения точки, где s(t) – путь, пройденный ею за время t. Тогда про-
изводная от пути s по времени движения t есть скорость движения v(t), то
есть v(t) = s′ (t). В этом заключается физический(механический) смысл про-
изводной.
С геометрической точки зрения значение производной функции в точке хо равно тангенсу угла α наклона касательной к кривой
в точке
,
то есть
.
Пример. Найти угловой коэффициент касательной к параболе
в точке А(1;
0).
Решение. Исходя из геометрического смысла производной функции
имеем:
Найдем производную данной функции.
По определению производной имеем:
=
.
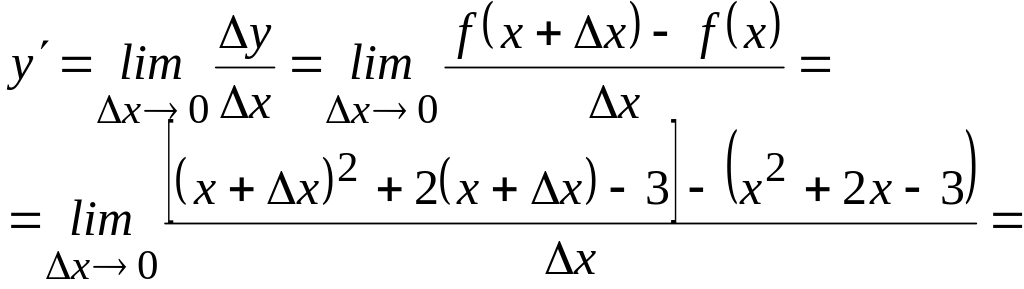
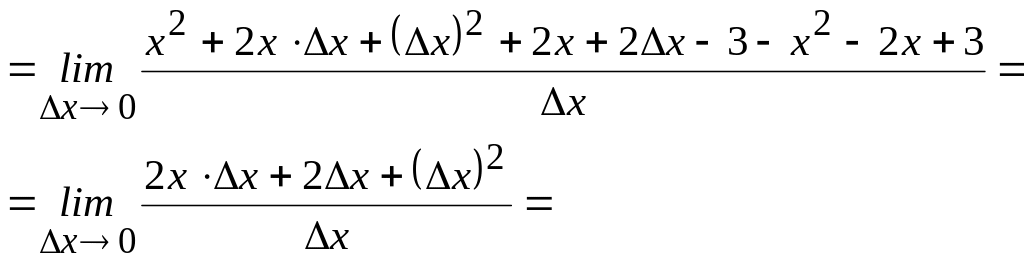
Тогда
.
Связь между непрерывностью и дифференцируемостью функции ус-
тановлена следующей теоремой.
Теорема. Если функция дифференцируема в некоторой точке, то она
в этой точке непрерывна.
Обратное утверждение,
вообще говоря, неверно. Так, например,
функция
непрерывна в точке х
= 0, но не
имеет в этой производной, так как
односторонние пределы
и
в точке х =
0
не совпадают:
;
.
2. Правила и формулы дифференцирования.
Пусть u=u(x) и v=v(x) – функции, дифференцируемые в точке хо;
v(xo) ≠ 0; С – постоянная величина. Справедливы следующие теоремы, на-зываемые правилами дифференцирования.
Теорема 1. Производная постоянной равна нулю, то есть
С′ = 0. (I)
Теорема 2.Производная суммы конечного числа дифференцируемых
функций равна сумме производных слагаемых функций, то есть
.
(II)
Теорема 3. Производная произведения двух дифференцируемых
функций равна сумме произведения производной первого множителя на
второй и первого множителя на производную второго, то есть
.
(III)
Теорема 4. Постоянный множитель можно выносить за знак произ-
водной, то есть
.
(IV)
Теорема 5. Производная частного двух дифференцируемых функций
равна дроби, числитель которой есть разность между произведением про-
изводной числителя на знаменатель и произведением числителя на произ-
водную знаменателя, а знаменатель дроби есть квадрат знаменателя дан-
ной дроби, то есть
.
(V)
Теорема
6. Производная
сложной функции
,
где
по
по независимому аргументу x равна произведению производной функции у
по промежуточному аргументу u на производную функции u по независи-
мой переменной х, то есть
.
(VI)
Исходя из определения производной и указанных выше теорем мож-
но вывести следующие формулы производных основных элементарных
функций (табличные формулы):
(1).
.
(2).
.
(3).
.
(4).
.
(5).
.
(6).
.
(7).
.
(8).
(9).
(10).
.
(11).
.
(12).
(13).
.
Если u = х, то u′ = 1.
Пример 1. Найти производные данных функций:
а)
;
б)
.
Решение.
а)
Преобразуем данную функцию:
.
Применим формулы (II), (I) и (1):
.
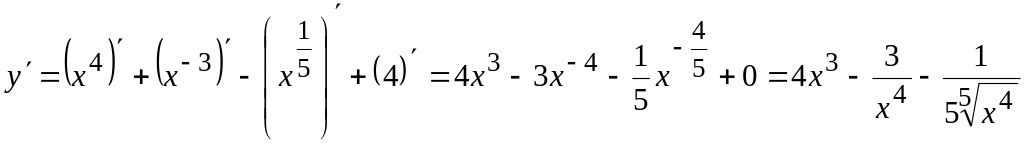б) Применяем формулы (III), (1), (8):
.
Пример 2. Найти производные данных функций:
а)
; б)
.
Решение.
а) применяем правило (VI) дифференцирования сложной функции и
табличные формулы:
.
б) Последовательно применяем правило (VI):
