
Лекция 2.
Тема лекции: Применение дифференциального исчисления
к исследованию функций.
Оглавление:
1. Возрастание и убывание функции
2. Экстремумы функции.
3. Наибольшее и наименьшее значения функции на отрезке.
4. Выпуклость и вогнутость кривой. Точки перегиба.
5. Асимптоты кривой.
6. Схема исследования функции и построения ее графика.
Цели лекции: использовать производную для исследования функций и решения экстремальных задач
После изучения рассматриваемого материала Вы сможете исследовать функции методами дифференциального исчисления и применять эти методы для прикладных задач.
Информационные источники.
1.Пискунов Н.С. Дифференциальное и интегральное исчисления.
Т. 1,2. М.; Наука (любое издание).
2. Лычкин В.Н.Высшая математика. Учебное пособие. РГАЗУ, 2011.
3. Лычкин В.Н.Высшая математика в задачах. Учебное пособие. РГАЗУ, 2009.
1. Возрастание и убывание функции.
Справедливы следующие теоремы.
Теорема
Ролля . Если
функция
![]() непрерывна на отрезке
непрерывна на отрезке
[a; b], дифференцируема на интервале (a; b) и на концах отрезка принима-
ет равные значения,
то есть
![]() ,
то на интервале (a;
b)
найдется по
,
то на интервале (a;
b)
найдется по
крайней мере одна
точка с
, в которой производная
![]() .
.
Теорема Ролля
имеет следующее геометри-
ческое толкование.
Если кривая
имеет
касательную в
каждой точке интервала (a;
b)
и
,
то на кривой
найдется по
крайней мере одна
точка С(c;
касательная CD
параллельна оси Ох (рис. 1).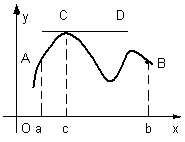
![]() ),
в которой
),
в которой
Рис. 1
Теорема Лагранжа . Если функция непрерывна на отрезке [a; b],
дифференцируема на интервале (a; b), то на этом интервале найдется хотя
бы одна точка с, для которой выполнено равенство
![]() или
или
![]() .
.
Теорема Лагранжа
геометрически тракту-
ется так: если
кривая
имеет касатель-
ную во всех точках
интервала (a;
b),
то на дуге
АВ существует по
крайней мере одна точка
С(с;
),
в которой касательная к этой кривой
параллельна хорде
АВ (рис. 2).

Рис. 2
Теорема Ролля является частным случаем теоремы Лагранжа, когда
.
Определение
1.Функция
![]() называется возрастающей
на интер-
называется возрастающей
на интер-
вале (а; b), если большему значению аргумента соответствует большее зна-
чение функции, то
есть если а
< x
1 <
x
2<b,
то
![]() .
.
Определение 2. Функция называется убывающей на интерва-
ле (a; b), если большему значению аргумента соответствует меньшее зна-
чение функции, то
есть если a
< x1
< x2
< b,
то
![]() .
.
Теорема 1. (Достаточный признак возрастания функции)
Если производная
![]() дифференцируемой функции
поло-
дифференцируемой функции
поло-
жительна в каждой точке интервала (a; b), то функция возрастает на этом интервале.
Доказательство. Из теоремы Лагранжа следует, что .
Произвольно выберем значения аргумента х1 и х2 такие, что a < x1 < x2 < b. Применим теорему Лагранжа для функции на отрезке [x1; x2] :
![]() ,
где
,
где
![]() .
.
Так как
![]() и
и
![]() ,
то
,
то
![]() ,
и следовательно
,
и следовательно
![]() .
Это означает, что на рассматриваемом
интервале
.
Это означает, что на рассматриваемом
интервале
![]() функция
возрастает.
функция
возрастает.
Теорема 2. (Достаточный признак убывания функции)
Если производная дифференцируемой функции отрицательна в каждой точке интервала (a; b), то функция убывает на
тельна в каждой точке интервала (a; b), то функция убывает на этом интервале.
Доказательство аналогично приведенному выше.
Пример. Найти интервалы возрастания и убывания функции
![]() .
.
Решение. Для нахождения интервалов возрастания и убывания дан-
ной функции воспользуемся приведенными выше теоремами.
Продифференцируем данную функцию:
![]() .
.
Определим интервалы знакопостоянства производной у′, используя
метод интервалов, по которому на числовой оси (рис. 3) отметим точки
х =
1 и х
= 3, в которых производная данной функ-
ции равна нулю.
Эти точки разбивают числовую ось на
три интервала: (- ∞; 1), (1; 3), (3; ∞).
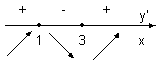
Рис. 3
В первом и третьем интервалах производная у′
положительна, поэтому функция здесь возрастает, на втором ин-
тервале у′ отрицательна и данная функция убывает.
