§5. Комплексная форма ряда Фурье. Интеграл Фурье.

1. Комплексная форма тригонометрического ряда Фурье.

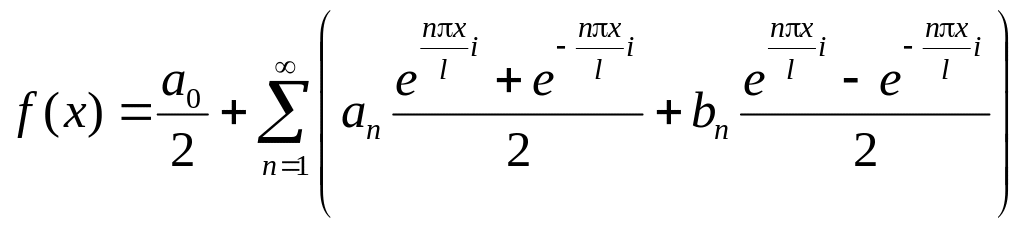
Пусть

(1) – ряд Фурье в комплексной форме.

Объединим 3 формулы: (2). Коэффициент - амплитуда.

- волновые числа, совокупность всех волновых чисел называется спектром,  гармоники.

2. Комплексная форма интеграла Фурье.

Пусть - кусочно-непрерывная на R, и абсолютно интегрируема на этом множестве, т.е. сходится интеграл . Совокупность таких функций обозначают - линейное пространство.

Для любого промежутка , может быть разложено в ряд Фурье. Запишем этот ряд, подставив в него коэффициенты из (2): . Преобразуем ее следующим образом: .

(3).

Правая часть равенства (3) представляет собой интегральную сумму функции .

Так как интегрируема на промежутке , то l можно выбрать сколь угодно большим. При (4),

интеграл в правой части равенства (4) – интеграл Фурье в комплексной форме

(5).

(6).

Функция называется преобразованием Фурье функции . В свою очередь - обратное преобразованием Фурье. То есть, преобразование Фурье представляет собой отображение, заданное на множестве функций, т.е. это оператор.

играет такую же роль, как и коэффициент Фурье и называется спектральной функцией.

Непериодические функции соответствуют непериодическим спектрам.

3. Тригонометрическая и вещественная формы интеграла Фурье.

Преобразуем интеграл Фурье, использую формулу Эйлера:

(7) - тригонометрическая форма интеграла Фурье.

Формула (7) упрощается, так как - является четной по U, - нечетная. После вычисления 1 интеграла по t свойство четности/нечетности сохраняется. Вычислив 2 интеграл по U, который вычисляется по симметричному промежутку с учетом четности / нечетности слагаемых можно представить в следующем виде:

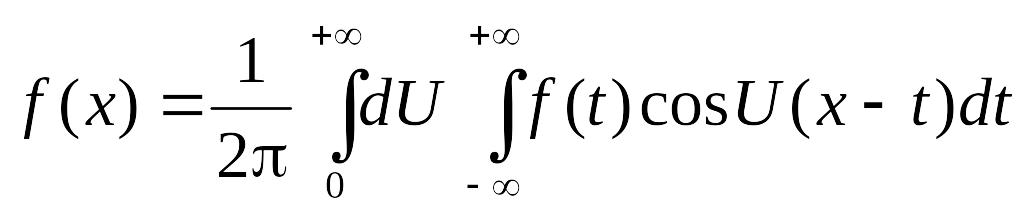(8) - интеграл Фурье в вещественной форме.

Преобразуем уравнение (8) в следующий вид (9), где .

.

4. Тригонометрическая форма преобразования Фурье. Sin – и Cos – преобразования Фурье.

Используя формулу Эйлера для представления экспоненты комплексного числа, преобразования Фурье можно записать в виде:

.

Если - нечетная, то интегралы которые содержат Сos будут = 0. Тогда

.

Умножим первое из уравнений на i и введем обозначения.

(10)

(11)

(10) и (11) Cos – преобразования Фурье.

Если - четная, то интегралы которые содержат Sin будут = 0. Тогда (12)

(13)

(12) и (13) Sin – преобразования Фурье.

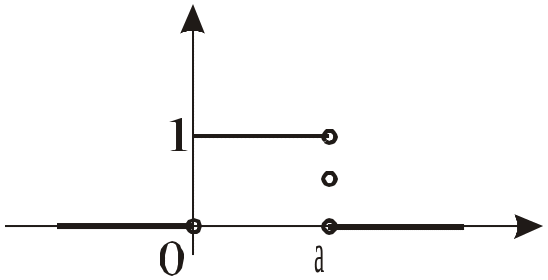
Пример.

Найти Сos и Sin преобразования Фурье.

.