
- •Дайте визначення та характеристику двомірного дискретно косінусного перетворення.
- •Д айте визначення та характеристику дискретно сінусного перетворення.
- •18. !!! Неизвестно
- •Модифікування дерева у алгоритмі Хаффмана.
- •Переповнення лічильника у алгоритмі Хаффмана.
- •Спрощений варіант алгоритму Хаффмана стиску даних.
- •Метод арифметичного кодування даних.
- •Метод цілочисленого арифметичного кодування даних.
- •Статистична модель каналу системи зв'язку. Постановка задачі визначення оптимальної прийомної системи.
- •Загальне рішення задачі визначення оптимальної прийомної системи.
ЛК1
Стиск даних відноситься до будь-яких типів інф. Даних і пов'язаний з питанням зменшення надлишкової інформації в цих даних.
Розрізняють такі типи даних:
Текстові, характерні тим, що при обробці не допускаються втрати чи …
Зображення, характерні тим, що великий обсяг даних, сприймаються ці дані …. . Допускаються втрати чи зміни при перетворенні.
Мовні (ключові) сприймаються індивідуально кожним користувачем, тому допускаються втрати даних при перетворенні.
Аудіо файли, допускається погрішність при відновленні
Відповідно до типу даних використовуються різні алгоритми стиску даних.
Основні терміни та показники алгоритмів стиску
Розглядають методи адаптивного стиску та не адаптивного
Стиск без втрат та з втратами
Симетричний стиск або методи несиметричного стиску
Асиметричний: складний стиск при передачі і простий алгоритм при відновленні.
Методи стиску:
Статистичні методи стиску (формують коди відповідної статистики)
На основі перетворень
Коефіцієнт стиску визначається як відношенням розміру вихідного файлу до вхідного.
Ортогональне перетворення відноситься до стиску зображень, мови та аудіо файлів.
Цифрове зображення – це матриця розміром м*н, точка – пік сель, розрізняють безкольорові зображення або кольорові.
Виділяють наступні типи зображень:
Двоуровневый
Полутонові
Цвітові
Основні методи стиску зображень
Використання методу длінних серій
Зображення записується як послідовність пікселей і кодується спеціальним кодом (адаптивним арифметичним кодом), який базується на статистичні появи якості
Використовується перетворення зображення в результаті якого ми одержуємо коефіцієнт перетворення які відображають ті чи інші особливості зображення і можуть по різному кодуватися.
Дайте визначення та характеристику двомірного дискретно косінусного перетворення.
Д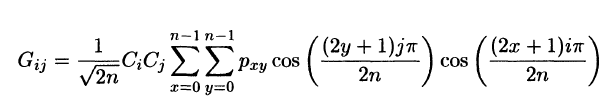 вомірне
дискретно косинусне перетворення. Пряме
:
вомірне
дискретно косинусне перетворення. Пряме
:
при о < i , j < п — 1. Изображениеразбивается на блоки пикселов
Рхуразмерап х п ( внашемпримереn = 8), и уравнения (3.9) используются
для нахождениякоэффициентовGijдля каждого блока
пикселов. Еслидопускаетсячастичнаяпотеряинформации, то
коэффициентыквантуются. Декодер восстанавливаетсжатый блок
данных (точно илиприближенно), вычисляяобратное DCT (IDCT)
п о
формуле
о
формуле
G0,0будет самым большим, остальные коэфициенты значительно меньше. Это происходит как для коррелированных данных так и для случайных.
Д айте визначення та характеристику дискретно сінусного перетворення.
(Для дискретно синусного преобразования в формуле вместо cos поставить sin)
Для того, чтобы понять разницумежду DCT и DST, рассмотрим
одномерный случай. Одномерное DCT, (см. уравнениевыше),
используетфункциюcos((2t + 1)f*pi/16) при f = 0 , 1 , . . . , 7. Для первого
значения, равногоf = 0, этафункцияравнаcos(0) = 1. Этот
член оченьважен; он производиткоэффициент DC, которыйсоответствует
среднемузначению восьми преобразуемым величинам. По
аналогии, DST основано на функцииsin ((2t + 1)f*pi/16) котораяравна
sin(0) = 0 при f == 0, то есть, этот член не вноситникакого
вклада в преобразование, то есть DST не имееткоэффициент DC.
Помимо этого недостатка, так же в DST энергия входных данных нигде не концентрируется, она распределяется по разнымкоэфициентам.
Так же квантование коэфициентов преобразования уменьшает качество восстановления.
Дайте визначення та характеристику вейвлетного перетворення Хаара.
Перетворення Хаара запис на функціях k(x).
Правила:
1 Ф-язадаєтсяx![]() [0,1]
[0,1]
2 k=0,1…..n-1
3 N=2n
Значення k необхідно подати у вигляді
k = 2p+q-1
0≤p<n-1
q=0 або 1, якщо р=о
1≤q≤2p якщо p≠0
Для перетворення Хаара також можна використати ф-ю шкали і значення вейвлета.
Будь-яка послідовність f(t) може бути записана у вигляді ряду.
f(t)=![]()
![]()
(t)=
![]()
Формальне подання вейвлет перетворення Хаара.
Дайте визначення та характеристику перетворення Уолша-Адамара.
Перетворення Уолша-Адамара визначається спеціальними матрицями з властивостями:
H(u,v)
=![]()
N-розмір перетворення
n=
![]()
![]() – i-ий
біт в розкладі значення Х
– i-ий
біт в розкладі значення Х
![]() -
обчислюється з використанням рекурентних
співвідношень
-
обчислюється з використанням рекурентних
співвідношень
Обчислення матриці перетворення Уолша – Адамара є швидким. По розрахункам перетворення Уолша-Адамара являється меньш ефективним ніж ДКП, але цей висновок вимагає досліджень. Сам алгоритм стиску подібний до ДКП.
Матрична форма вейвлет перетворення Хаара.
Матриця перетворення являєте ортогональною. Незалежно від методу перетворення маємо одне і теж середне число в крайньому верхньому лівому куті матриці. Інші елементи є малими числами. Масив чисел кодується з використання комбінації декількох методів. Перетворення на основі полусум та полуразниць має назву перетворення Хаара, яке є найпростішим велет перетворенням.
Визначення та обчислення вейвлетівДобеши.
Основною формою подання перетворень являється матрична форма. Матриці перетворення відносяться до класу ортогональних матриць, під діапазонні перетворення визначають ще одну форму перетворень на основі фільтрів аналізу та синтезу.
Фільтр визначається лінійним оператором з коеф. Для дискретного фільтру, це h(0), h(1), h(2)… В результаті обчислення маємо значення на виході
y(n)
= ![]() - Згортка двох послідовностей.
- Згортка двох послідовностей.
h(k)->H(L) – амплітудно-частотна хар-ка фільтра
В простому випадку існує 2 фільтри високочастотний(Н0) та низькочастотний(Н1).
Основним недоліком до побудови фільтрів є накладання деяких обмежень на їх коефіцієнти. Для 4-х коеф. Фільтру (a,b,c,d) можна визначити ортогональність у вигляді наступного рівняння.
(a,b,c,d)(d,-c,b,-a)=0
ad-bc+cb-da=0
16. Визначення та характеристика під діапазонних перетворень
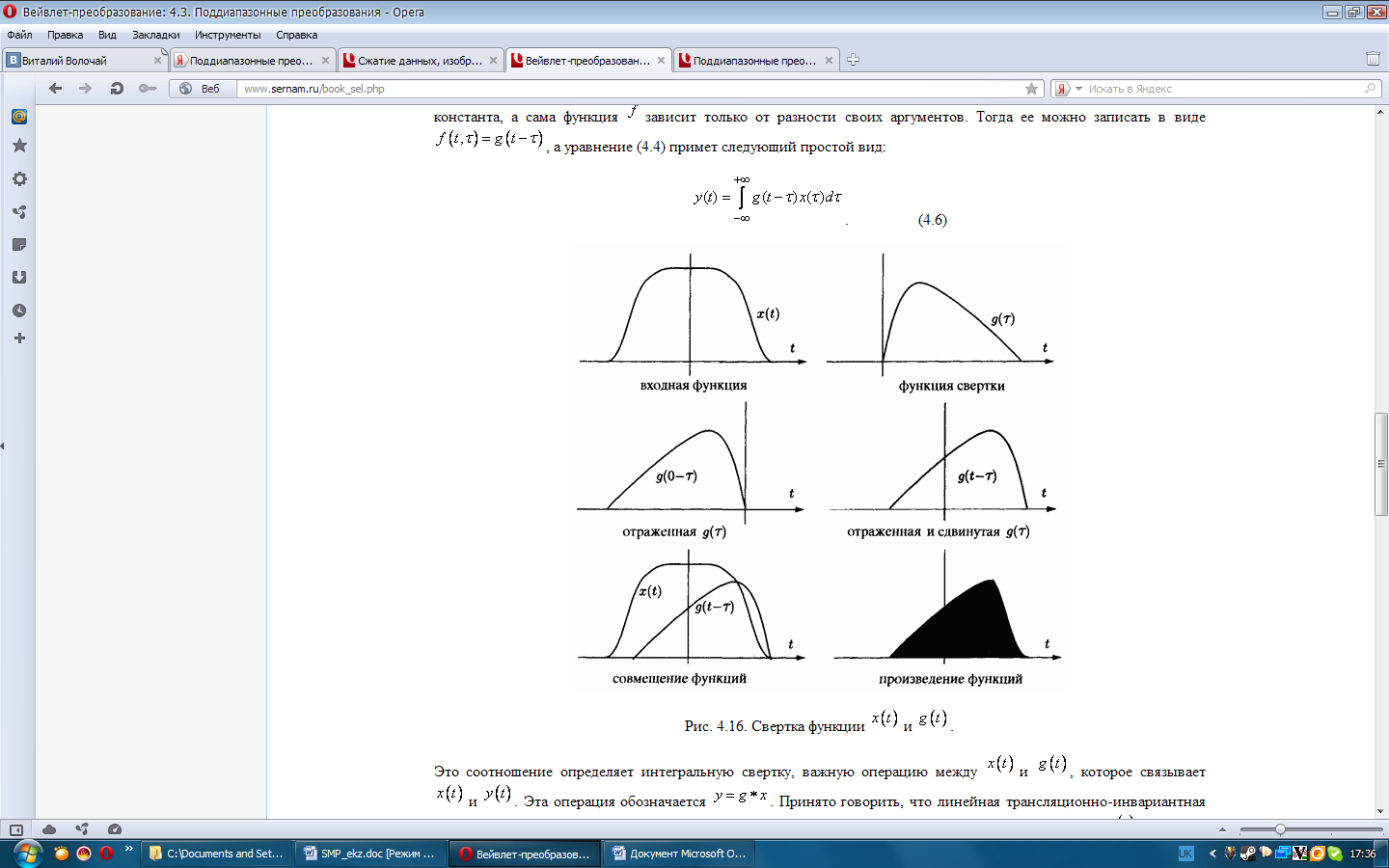
С другой стороны, вейвлетные преобразования являются поддиапазонными преобразованиями. Их можно вычислять с помощью операции свертки исходных данных (будь то пикселы или звуковые фрагменты) и множества фильтров пропускания определенных частот. В результате поддиапазон охватывает некоторую часть полосы частот исходных данных.
Примерами поддиапазонных преобразований являются преобразование Хаара и преобразование методом «полусум и полуразностей».
Слово «свертка» означает совместное сворачивание величин или функций. Дискретная свертка двух векторов и , которая также является вектором, обозначается . Компоненты свертки вычисляются по формулам :
( f*g)i=∑j
fj
*
gi-j
f*g)i=∑j
fj
*
gi-j
Свертка имеет несколько важных свойств. Она удовлетворяет свойствам коммутативности, ассоциативности и дистрибутивности по сложению.
П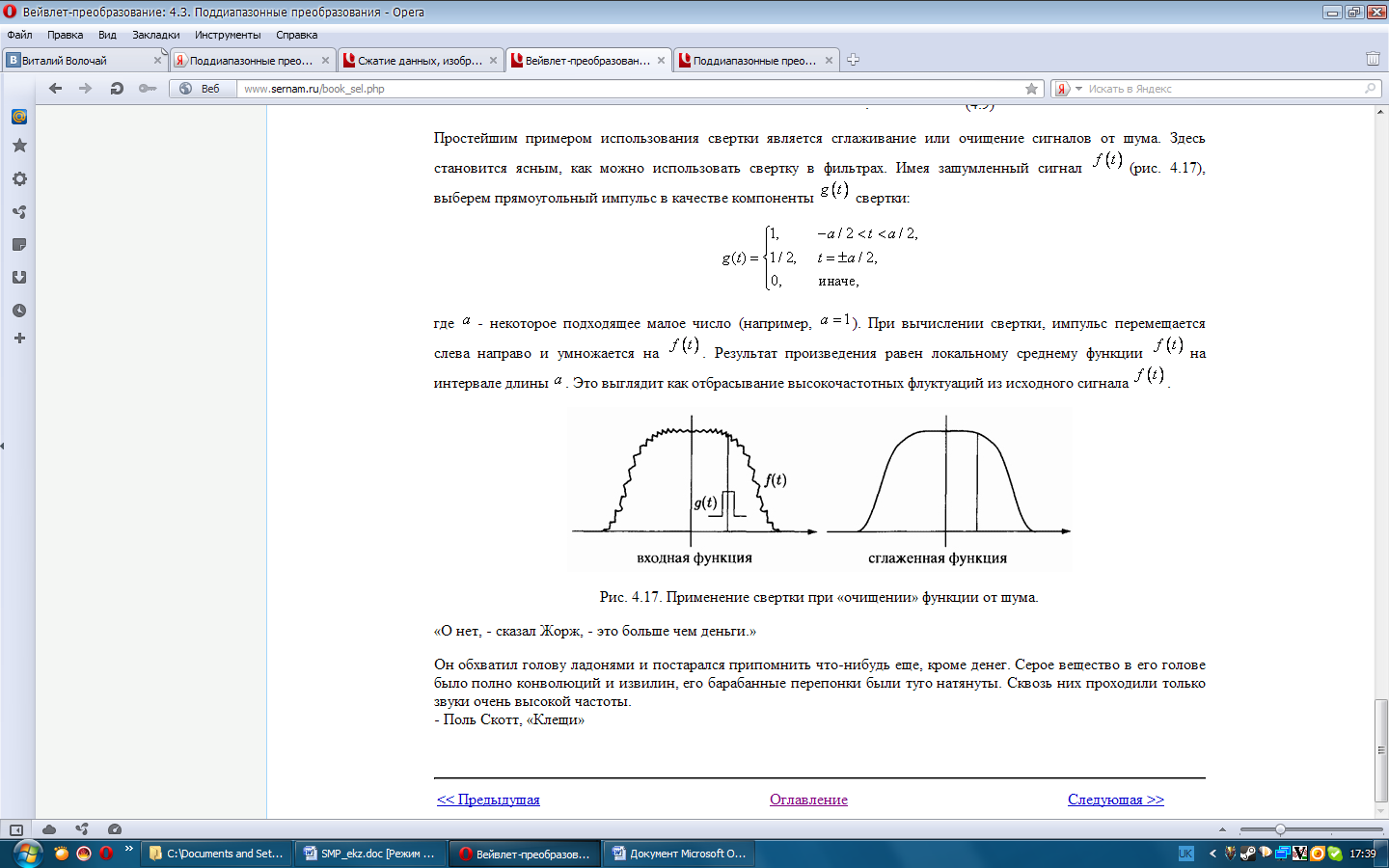 ростейшим
примером использования свертки является
сглаживание или очищение сигналов от
шума. Здесь становится ясным, как можно
использовать свертку в фильтрах.
ростейшим
примером использования свертки является
сглаживание или очищение сигналов от
шума. Здесь становится ясным, как можно
использовать свертку в фильтрах.
17. Визначення банку фільтрів аналізу перетворень. Обчислення коефіцієнтів банку фільтрів.
Преобразование Хаара можно интерпретировать как банк, состоящий из двух фильтров: один пропускает низкие частоты, а другой высокие.
Фильтром называется линейный оператор, определяемый с помощью коэффициентов фильтра h(0), h(1), h(2),… . Этот оператор применяется к входному вектору x, в результате чего получается выходной вектор y :
y(n)= ∑k h(k)* x(n-k)=h*x
На рис. показана основная идея банка фильтров. Там изображен банк анализа, состоящий из двух фильтров: низкочастотного и высокочастотного . Низкочастотный фильтр использует свертку для удаления из сигнала высокочастотной составляющей. Он пропускает низкие частоты. А высокочастотный фильтр делает все наоборот. Он удаляет из сигнала высокие частоты. Вместе они разделяют входной сигнал на поддиапазоны частот.
П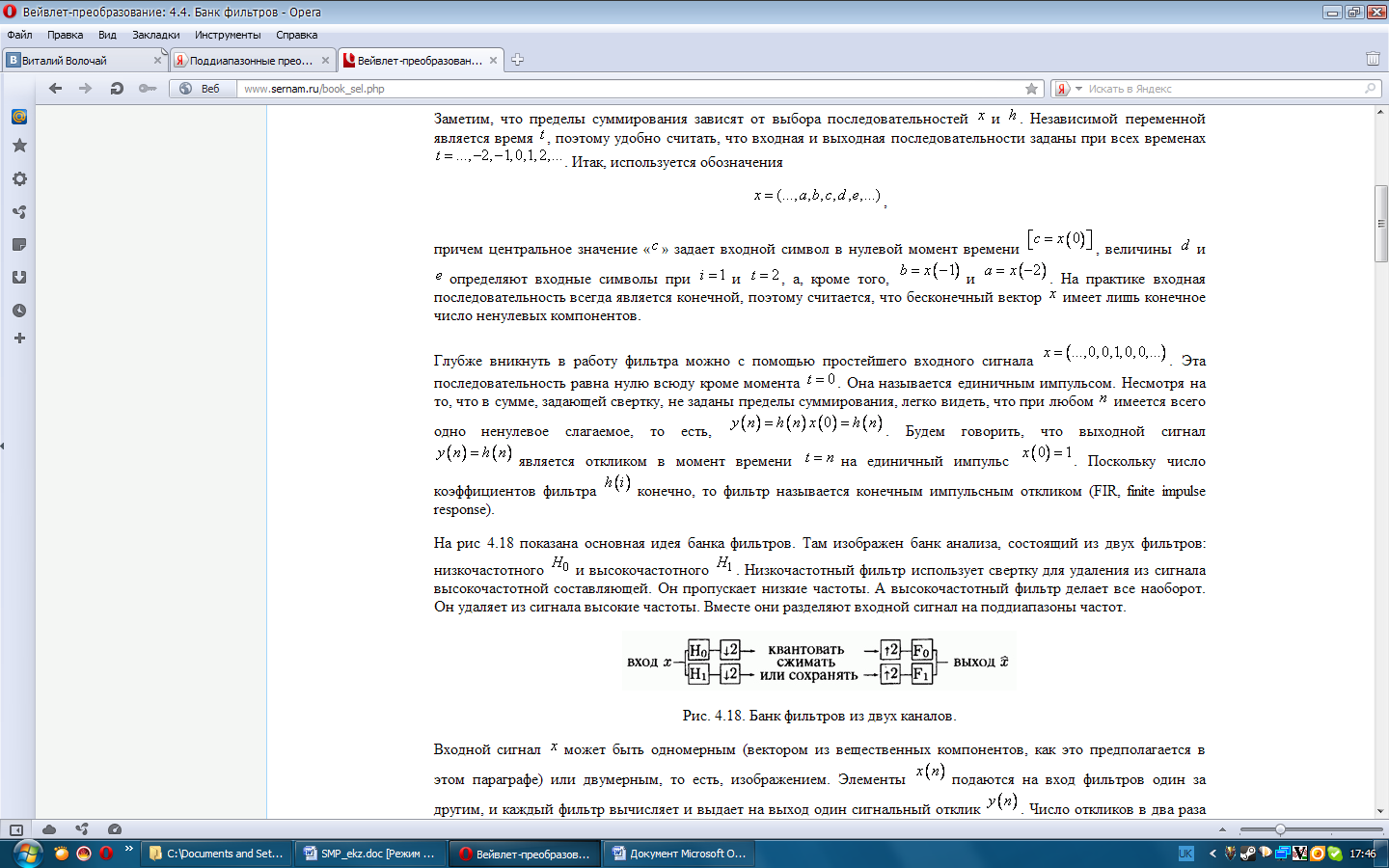 ример:
ример:
Y[n]=a[n]+d[n].
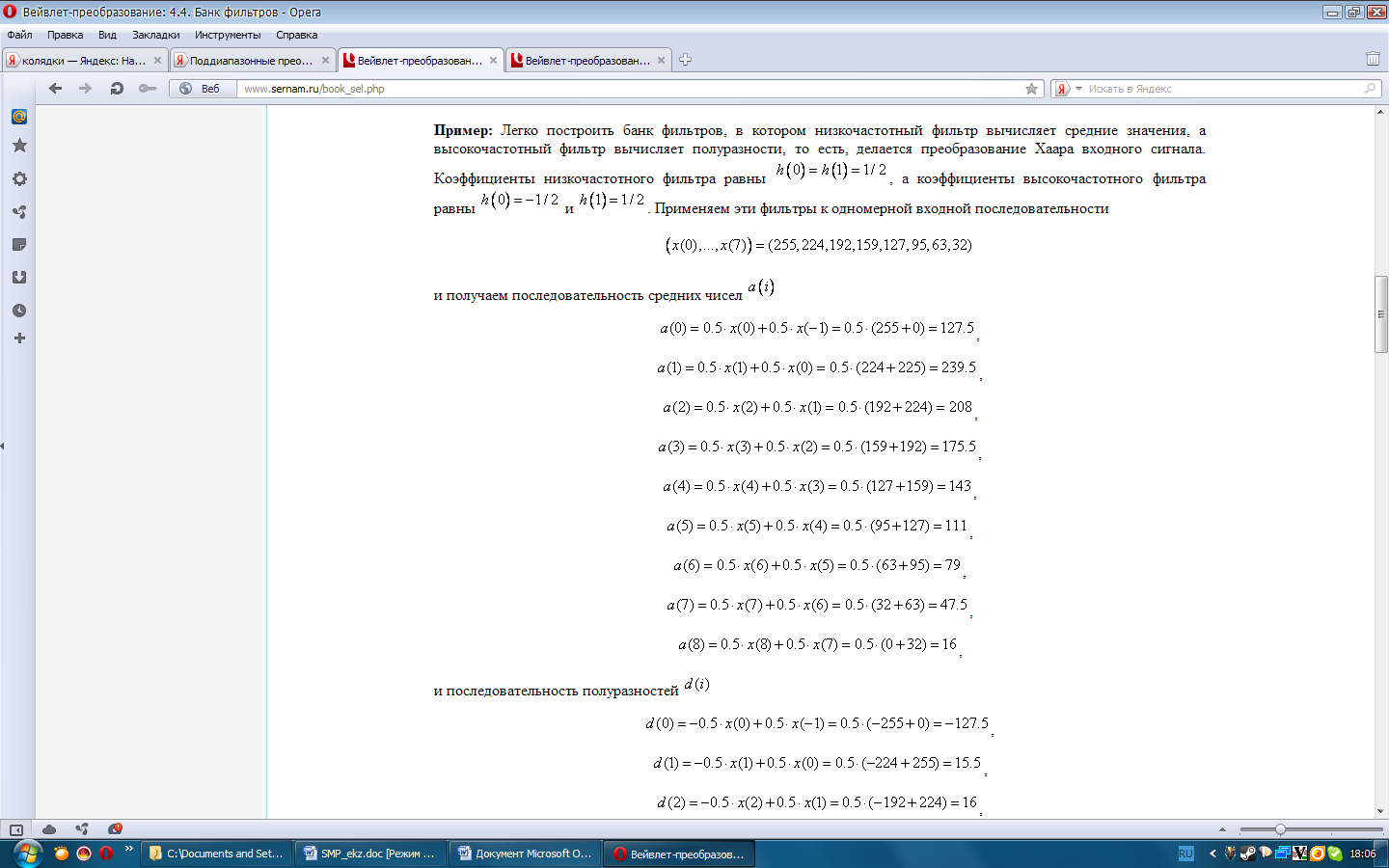
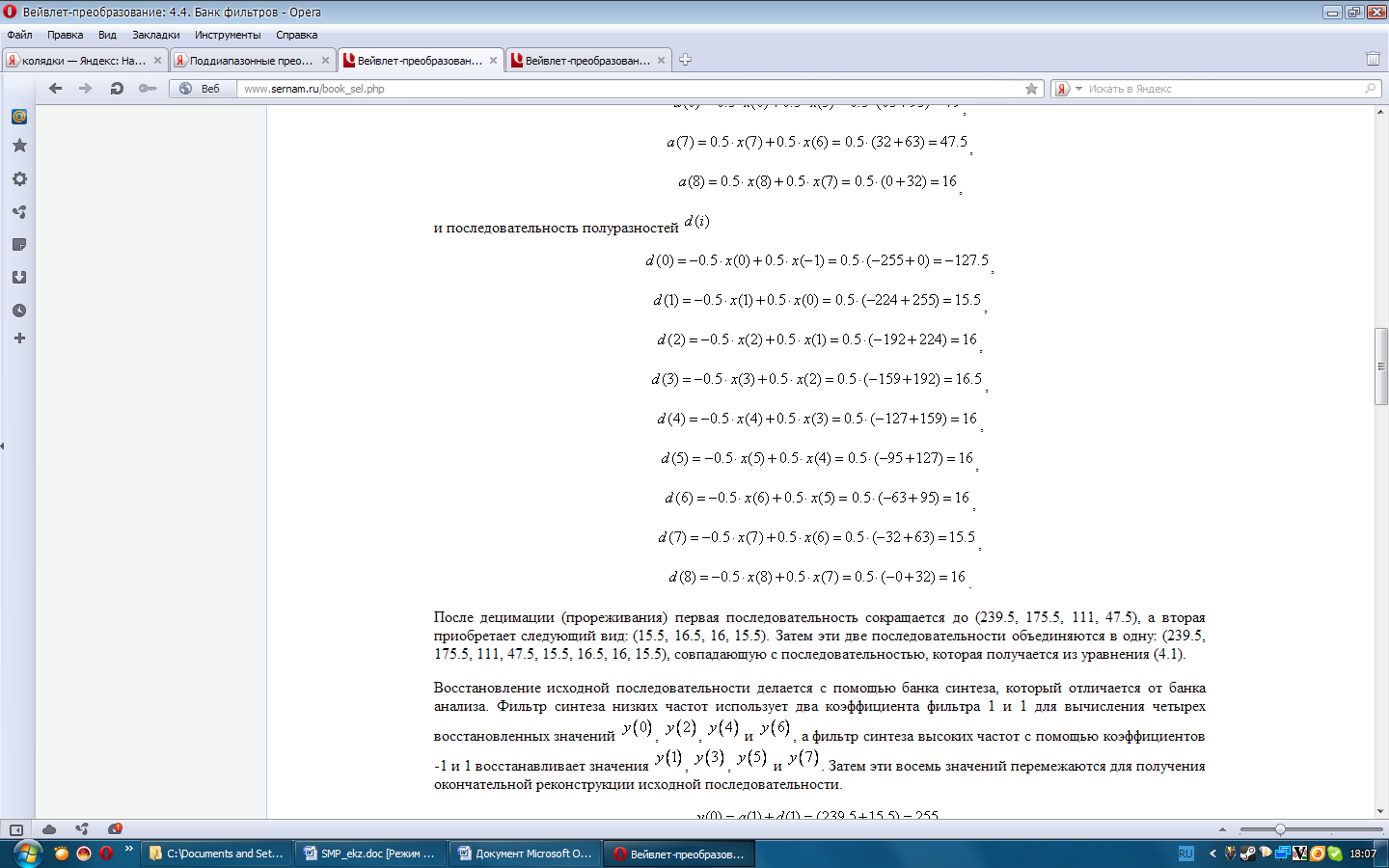
Правила вычисления коэффициентов фильтра
1. Нормализация: Вектор h0 имеет единичную длину.
2. Ортогональность: Для любого целого числа i , удовлетворяющего неравенству 1<=i<N/2, вектор, состоящий из первых 2i элементов h0 , должен быть ортогонален вектору, составленному из последних 2i элементов того же вектора h0.
3. Вектор f0 состоит из компонентов вектора h0 , записанных в обратном порядке.
4. Вектор h1 является копией f0, но с обратными знаками у компонент на нечетных позициях (первой, третьей и т.д.). Формально это можно выразить как покомпонентное умножение вектора h1 на вектор (-1,1,-1,1,…) .
5. Вектор f1 является копией h0 , но с обратными знаками у компонент на четных позициях (второй, четвертой и т.д.). То есть f1, равен h0 , умноженному на (1,-1,1,-1,..).
