
Вопрос 1
Теорема
1.
Предел
постоянной равен самой постоянной.
![]()
Теорема 2. Функция не может иметь двух различных пределов в одной точке.
Теорема
3.
Если
каждое слагаемое алгебраической суммы
функций имеет предел при
![]() ,
то и алгебраическая сумма имеет предел
при
,
причем предел алгебраической суммы
равен алгебраической сумме пределов.
,
то и алгебраическая сумма имеет предел
при
,
причем предел алгебраической суммы
равен алгебраической сумме пределов.
![]()
![]()
![]()
![]() .
.
Теорема 4. Если каждый из сомножителей произведения конечного числа функций имеет предел при , то и произведение имеет предел при , причем предел произведения равен произведению пределов.
![]()
![]()
![]()
Теорема 5. Если функции f(x) и g(x) имеют предел при ,
причем
![]() ,
то и их частное имеет предел при
,
причем предел частного равен частному
пределов.
,
то и их частное имеет предел при
,
причем предел частного равен частному
пределов.
![]()
Признаки существования предела:
1.
Если ![]()
![]() и
и ![]()
![]() ,
то
,
то ![]()
2. Монотонная и ограниченная последовательность имеет предел.
3. Числовая последовательность (xn) имеет конечный предел тогда и только тогда, когда
![]()
![]()
![]()
![]()
![]()
Билет №4
Вопрос 1
Замеча́тельные преде́лы — математические тождества со взятием предела. Особенно известны:
Первый замечательный предел:
![]()
Второй замечательный предел:
![]()
Билет №5
Вопрос 1
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Связь между непрерывностью и дифференцируемостью функции. Если функция f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.
Билет №6
Вопрос 1
Правило вычисления производных
Если
функции f
и g
имеют конечные производные при
![]() ,
то:
,
то:
1)
![]()
![]() -
постоянные;
-
постоянные;
2)
![]()
![]() ;
;
3)
![]()
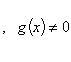 .
.
Основные правила дифференцирования
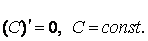
 (справедлива
для любого конечного числа слагаемых).
(справедлива
для любого конечного числа слагаемых).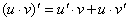 .
.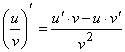 .
.
а)
![]() .
.
б)
![]() .
.
Билет №7
Вопрос 1
Основные теоремы дифференциального исчисления
Кольцо непрерывных на [a,b] и гладких на (a,b) функций обладает рядом важных свойств:
Теорема Ролля: если f(a) = f(b) = 0, то имеется точка
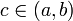 максимума
или минимума, в которой f' обращается в
нуль.
максимума
или минимума, в которой f' обращается в
нуль.Теорема Лагранжа: существует такая точка , что
![]()
Теорема Коши: если
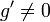 на
(a,b),
то существует такая точка
,
что
на
(a,b),
то существует такая точка
,
что
![]()
Правило Лопиталя
В
математическом
анализе
правилом
Лопита́ля
называют метод нахождения пределов
функций,
раскрывающий неопределённости вида 0
/ 0 и
![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
Правило говорит, что если функции f(x) и g(x) обладают следующим набором условий:
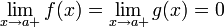 или
или
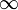 ;
;
 ;
;
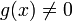 в
некоторой окрестности точки a,
в
некоторой окрестности точки a,
тогда
существует
![]() .
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).
.
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).
Билет №8
