Задание n 9 Тема: Уравнения Максвелла

Физический смысл уравнения Максвелла заключается в следующем …

			изменяющееся со временем магнитное поле порождает вихревое электрическое поле
			источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле
			«магнитных зарядов» не существует: силовые линии магнитного поля замкнуты
			источником электрического поля являются свободные электрические заряды

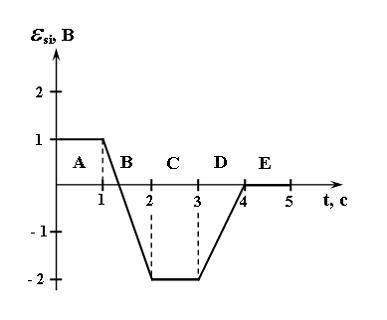
Задание n 10 Тема: Явление электромагнитной индукции

На рисунке представлена зависимость ЭДС индукции в контуре от времени. Магнитный поток сквозь площадку, ограниченную контуром, увеличивается со временем по закону (а, b, c – постоянные) в интервале …

			В
			С
			А
			D
			Е

Решение: В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: . Следовательно, если магнитный поток увеличивается со временем по закону , то ЭДС индукции будет убывать со временем по линейному закону, что имеет место в интервале В.

Задание n 11 Тема: Элементы специальной теории относительности

На борту космического корабля нанесена эмблема в виде геометрической фигуры: 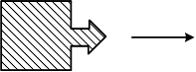Если корабль движется в направлении, указанном на рисунке стрелкой, со скоростью, сравнимой со скоростью света, то в неподвижной системе отсчета эмблема примет форму, указанную на рисунке …

Решение: Из преобразований Лоренца следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета со скоростью, сравнимой со скоростью света, уменьшается в направлении движения. Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета, поэтому форма тела изменится, как показано на рисунке

Задание n 12 Тема: Динамика вращательного движения

Обруч скатывается без проскальзывания с горки высотой 2,5 м. Скорость обруча (в м/с) у основания горки при условии, что трением можно пренебречь, равна …

			5

Решение: Поскольку трением можно пренебречь, в рассматриваемой системе выполняется закон сохранения механической энергии: потенциальная энергия обруча на вершине горки равна кинетической энергии поступательного и вращательного его движений у основания горки: 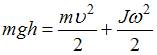. Учитывая, что момент инерции обруча и , получаем: . Отсюда