5. Интегралы группы четырёх.
1) Разложим знаменатель, квадратный трехчлен:
Введем новую переменную
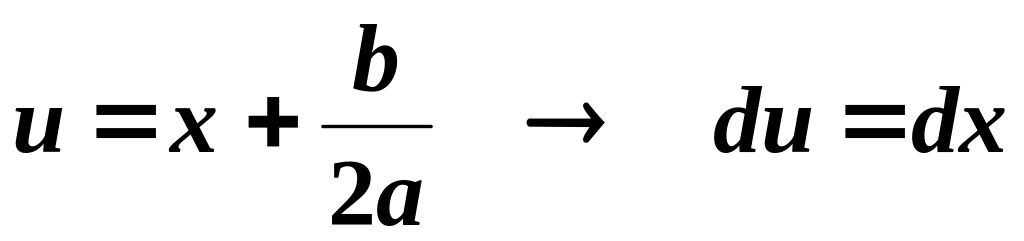
Тогда знаменатель будет иметь вид:
Рассмотрим
вначале случай, когда
.
При этом
.
Следовательно
Или, возвращаясь к старым переменным
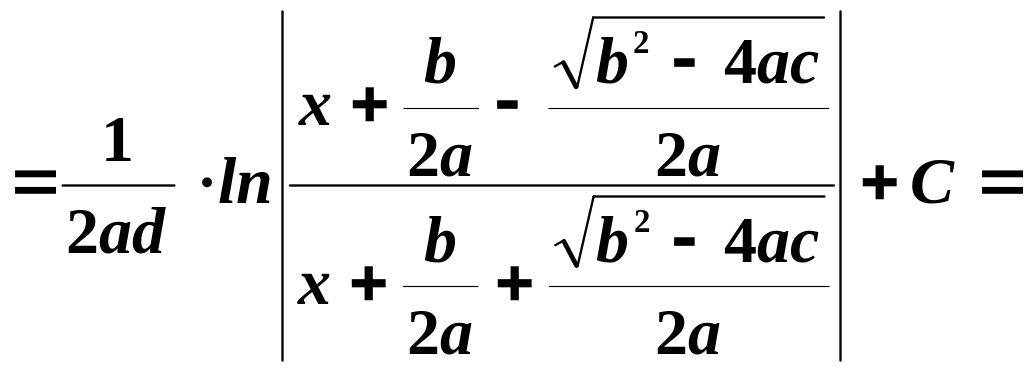
Преобразовывая, получим:
Теперь
рассмотрим случай, когда
.
Квадратный трехчлен представим в виде:
Следовательно
Опять возвращаясь к старым переменным, получим
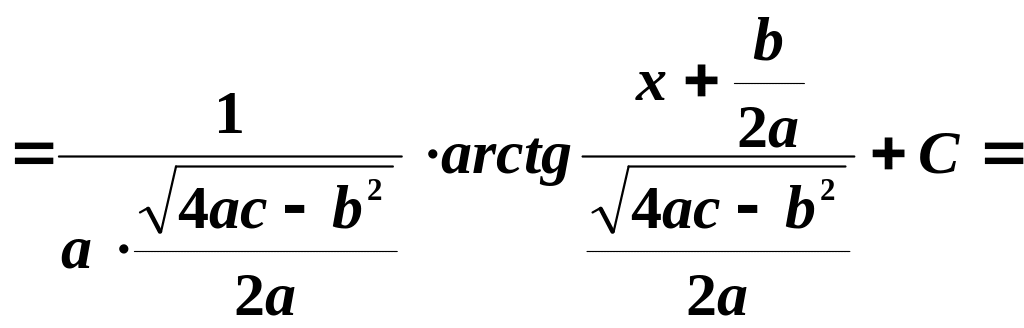
Преобразовывая, найдем:
Рассмотрим теперь второй интеграл.
Или
Рассмотрим
теперь третий интеграл. Используя
разложение квадратного трехчлена, и,
заменяя переменную
,
запишем:
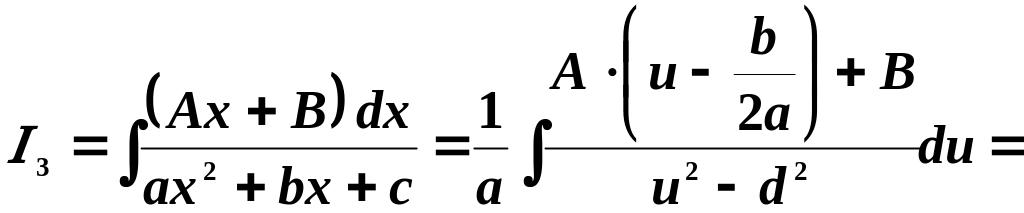
Полученное выражение представим в виде двух интегралов
В
дифференциал первого интеграла внесем
множитель
Возьмем интегралы
Вернемся к старым переменным
Рассмотрим
теперь последний интеграл
.
Аналогично, Используя разложение
квадратного трехчлена, и, заменяя
переменную
,
запишем
Полученное выражение также представим в виде двух интегралов
В
первом интеграле под знак дифференциала
введем
,
взяв второй интеграл и возвращаясь в
нем к переменной
,
получим
Взяв первый интеграл, получим окончательно
6. Интегрирование по частям.
Известно,
что дифференциал от произведения
равен:
Проинтегрируем полученное равенство
Интеграл от дифференциала некоторой функции равен самой функции:
Меняя местами слагаемые, получим:
Это и есть формула интегрирования по частям.
Пример. Вычислить
интеграл
.
Решение.
Положим
;
.
Тогда
7. Интегрирование рациональных дробей.
Дробью называется выражение вида:
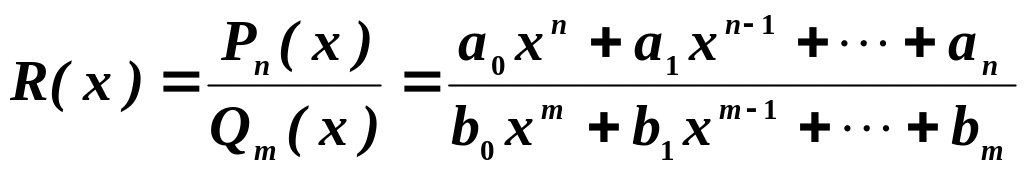
Дробь
- правильная, если
.
Дробь
- не правильная, если
.
Для того, чтобы проинтегрировать дробь надо разложить ее на простейшие дроби.
Простейшие дроби:
1.
2.
3.
4.
Интеграл от первой дроби - табличный интеграл:
1.
Интеграл от второй дроби - также табличный:
2.
3. Интеграл от третьей дроби см. интеграл группы четырёх.
4. Интеграл от четвертой дроби также см. интеграл группы четырёх.
Рассмотрим теперь дробь более общего вида.
Теорема.
Пусть
- правильная дробь, причем
.
Тогда эту дробь можно представить в
виде:
Доказательство
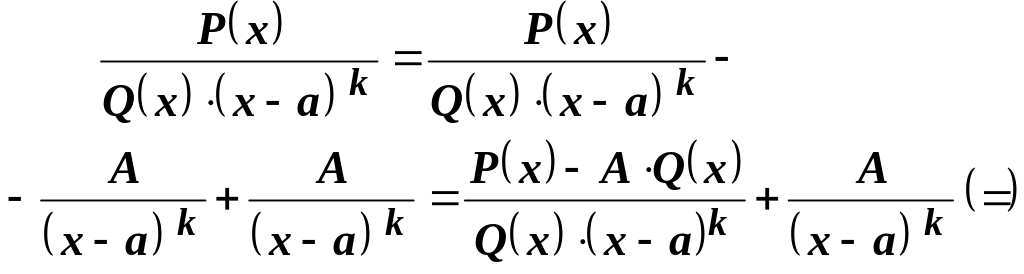
Далее,
выберем величину
равной:
.
Тогда получим, что
И если
,
то
То
есть
является корнем многочлена
.
В этом случае многочлен
можно представить в виде:
и, следовательно, далее запишем:
что и тр. док.
Следствие. Используя эту логику и дальше, можно записать:
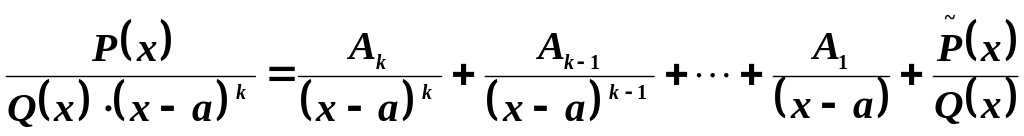
Теорема.
Пусть
- правильная дробь, причем
.
Тогда можно записать:
Следствие.
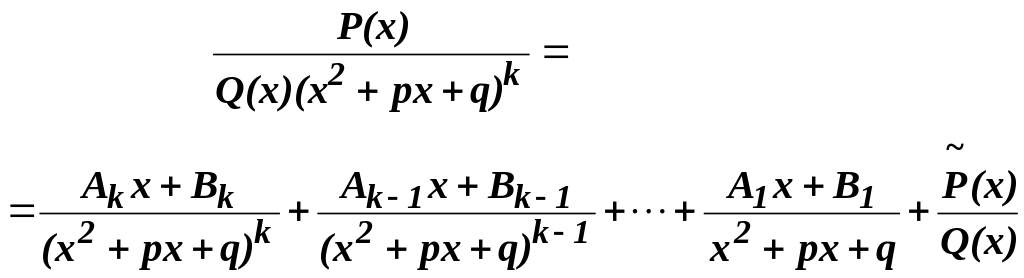
Таким образом, дроби общего вида сводятся к простейшим дробям.
8. Интегрирование тригонометрических выражений.
Для
нахождения интегралов вида
,
где
- рациональная функция, используют
универсальную тригонометрическую
подстановку
.
Тогда
.
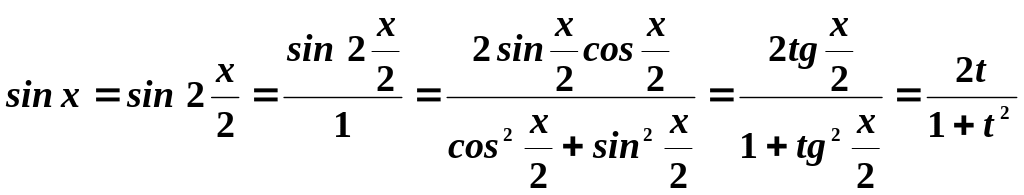
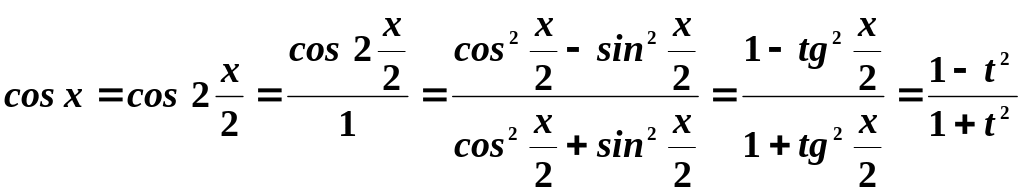
То есть подынтегральная функция приобретает вид:
Например,
возьмем интеграл
.
Для этого введем новую переменную
.
Тогда, как было показано выше
и
.
Подставим эти значения в искомый
интеграл:
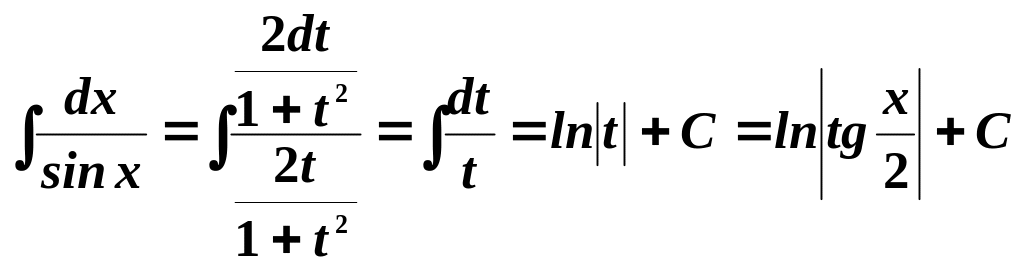
Пример
6.
Взять интеграл
.
Введем аналогичную замену переменных:
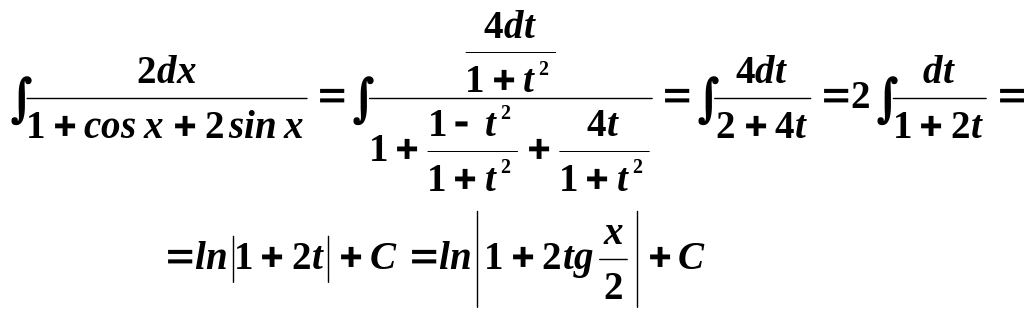
Частные случаи.
1. Интегралы вида
.
При
этом делаем замену
.
Тогда
2.
Интегралы вида
,
где
и
натуральные числа.
Данные
интегралы находятся с помощью
тригонометрических формул
,
,
,
если
и
– четные.
Если хотя бы одно из чисел и - нечетное, то от нечетной степени отделяется множитель и вводится новая переменная:
При
этом, если интеграл имеет вид
,
то
замена переменных:
.
Если
интеграл имеет вид
то
замена переменных:
.
Пример 7.
Взять интеграл
.
Замена переменных
.
Тогда
.
Наш интеграл примет вид:
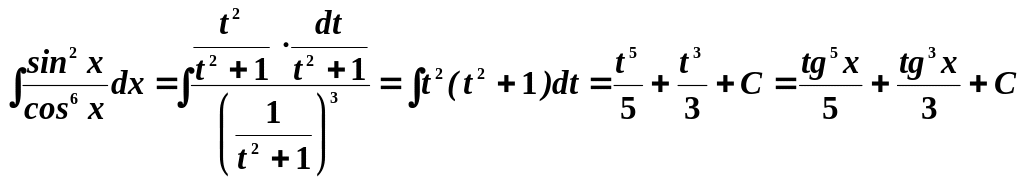
Пример 8.
Взять интеграл
.
Преобразуем подынтегральное выражение:
Косинус внесем под знак дифференциала, подынтегральную функцию преобразуем к следующему виду:
Возведем в куб подынтегральную функцию:
Сделаем замену переменных
и проинтегрируем:
Вернемся к старой переменной:
Пример 9.
Взять интеграл
.
Преобразуем подынтегральное выражение:
Возведем в куб:
Используем правило: интеграл от суммы равен сумме интегралов.
Сделаем преобразования под интегралами.
Возьмем уже "готовые" интегралы, а остальные преобразуем дальше
Сделаем дальнейшие преобразования
Взяв все интегралы, получим:
Перегруппировывая, получим:
Пример 10.
Взять интеграл
.
Преобразуем подынтегральное выражение
В первом интеграле учтем,
что
Во втором интеграле учтем,
что
Интеграл от суммы равен сумме интегралов
Учтем еще раз, что
Интеграл от суммы равен сумме интегралов
Далее
Окончательно
.
Используя известное тригонометрическое тождество
можно упростить взятие некоторых интегралов.
Например :
