
- •Четырехполюсники и их уравнения
- •1. Основные понятия и определения
- •2. Формы записи уравнений четырехполюсника. Матрицы четырехполюсника.
- •5. Симметричный четырехполюсник.
- •Электрические фильтры
- •1. Назначение и типы фильтров.
- •2. Основное неравенство фильтров.
- •Характеристическое сопротивление для т- и п-образной схем
2. Основное неравенство фильтров.
Получим условие, определяющее полосу пропускания фильтра – так называемое основное неравенство фильтра.
Уравнения формы А симметричного четырехполюсника в гиперболической форме имеют вид:
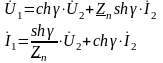
Коэффициент
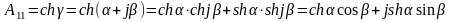 .
.
Результат получен, исходя из выражений:
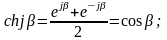
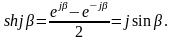
Получим коэффициент А11 по опытам холостого хода и короткого замыкания для Т- и П-образной схемы фильтра.
При холостом ходе на вторичных зажимах I2=0 и первое уравнение формы А имеет вид:
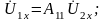 отсюда
отсюда
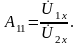
Для Т-образной схемы
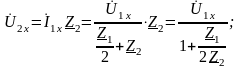
и
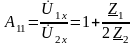 .
.
Для П-образной схемы
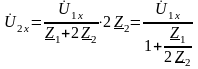
и
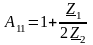 .
.
За счет принятых обозначений сопротивлений плеч выражение для А11 получилось одинаковым для Т- и П-образной схемы фильтра.
Сравнивая выражения для А11 в
гиперболической форме и полученный
результат, имеем
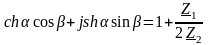 .
.
Для идеальных реактивных фильтров
отношение
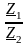 является вещественной величиной, поэтому
является вещественной величиной, поэтому
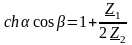 ,
а
,
а
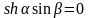 .
.
В зоне прозрачности
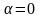 и
и
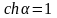 ,
,
тогда
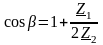 .
.
Поскольку
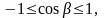 то
то
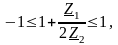
откуда
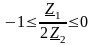 или
или
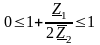 .
.
Это и есть основное неравенство
реактивных фильтров (условие пропускания
реактивных фильтров), которое
выполняется лишь тогда, когда
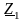 и
и
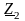 имеют различный характер. Если в
последовательном плече включена
индуктивность, то в параллельном должна
быть включена емкость и наоборот.
имеют различный характер. Если в
последовательном плече включена
индуктивность, то в параллельном должна
быть включена емкость и наоборот.
Граничные частоты полосы пропускания (частоты среза) определяются из условий
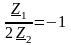 и
и
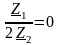 .
.
Частоты среза могут быть получены по частотной характеристике входного сопротивления фильтра, нагруженного согласованным сопротивлением.
3. Характеристическое сопротивление фильтра
Для симметричного четырехполюсника
(фильтра) согласованное сопротивление
 .
.
Определяя для Т- и П-образного фильтра сопротивления холостого хода и короткого замыкания, легко получить выражение для согласованных сопротивлений:
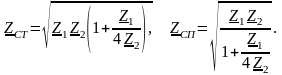
В полосе пропускания фильтра выражение
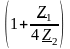 всегда является вещественной положительной
величиной; произведение
всегда является вещественной положительной
величиной; произведение
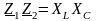 -
также вещественная положительная
величина. Поэтому в полосе пропускания
характеристическое сопротивление
является активным.
-
также вещественная положительная
величина. Поэтому в полосе пропускания
характеристическое сопротивление
является активным.
4. Фильтры типа К
Реактивные фильтры, удовлетворяющие
условию
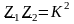 (т.е. произведение комплексных сопротивлений
плеч во всем диапазоне частот постоянно),
называются фильтрами типа К.
(т.е. произведение комплексных сопротивлений
плеч во всем диапазоне частот постоянно),
называются фильтрами типа К.
Учитывая, что сопротивления плеч
и
имеют разный знак (разный характер
элементов), то
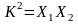 и условие пропускания фильтра принимает
вид:
и условие пропускания фильтра принимает
вид:
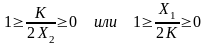
Характеристическое сопротивление для т- и п-образной схем
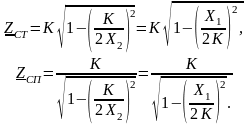
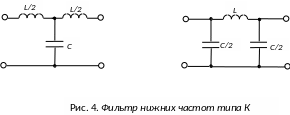
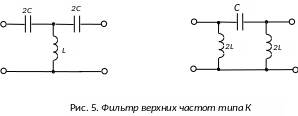
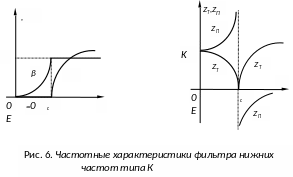
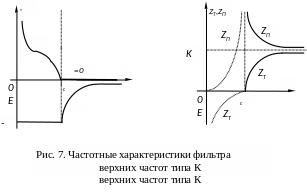
На рис. 4 и рис. 5 представлены схемы фильтров нижних частот, верхних частот, а на рис. 6 и рис. 7 – их частотные характеристики.
Характеристики таких фильтров с точки зрения физических процессов легко объяснить на основе поведения сопротивлений емкости, индуктивности, параллельного и последовательного контура в зависимости от частоты.
Преимуществом фильтров типа К является их простота, а также рост коэффициента затухания по мере удаления от граничной частоты (частоты среза) полосы пропускания.
Недостатки:
Резкое изменение характеристического сопротивления в зависимости от частоты в полосе прозрачности, вследствие чего согласование фильтра с нагрузкой осуществляется лишь в ограниченной части полосы пропускания.
Недостаточная крутизна нарастания затухания вблизи граничной частоты, что не обеспечивает четного разделения частот.
5. Фильтр нижних частот типа К
На примере фильтра нижних частот рассмотрим получение частоты среза, частотных зависимостей, характеристического сопротивления и расчет параметров фильтра.
Основное неравенство
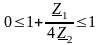 для фильтра нижних частот имеет вид:
для фильтра нижних частот имеет вид:
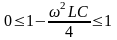
Отсюда граничные частоты (частоты среза):

Для получения
частотных зависимостей рассмотрим
соотношение
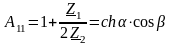 .
.
Для ФНЧ:
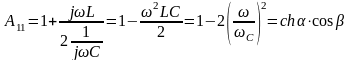 .
.
В зоне прозрачности и , тогда
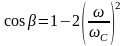 и
и
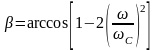 (А)
(А)
На левой границе полосы пропускания
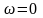 и
и
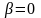 .
.
На правой границе полосы пропускания
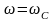 и
и
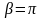 .
.
В зоне затухания
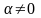 и
и
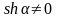 ,
но так как
,
но так как
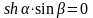 ,
то
,
то
 и коэффициент фазы может иметь значения
и коэффициент фазы может иметь значения
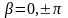 .
Так как на частоте среза
,
то и во всей зоне затухания
,
.
Так как на частоте среза
,
то и во всей зоне затухания
,
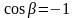 и равенство
и равенство
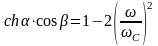 в зоне затухания принимает вид:
в зоне затухания принимает вид:
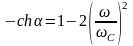 .
.
Отсюда
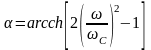 (В)
(В)
По полученным формулам А и В строятся
зависимости
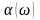 и
и
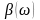 для фильтра нижних частот.
для фильтра нижних частот.
Характеристическое сопротивление фильтра нижних частот:
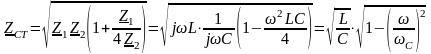 ,
,
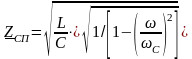 .
.
В зоне прозрачности при
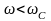 можно считать, что
можно считать, что
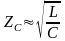 .
Таким образом согласованное сопротивление
нагрузки для фильтра нижних частот
.
Таким образом согласованное сопротивление
нагрузки для фильтра нижних частот
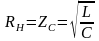 .
.
Для расчета фильтра нижних частот задаются сопротивлением нагрузки Rн и граничной частотой с.
В основе расчета лежат соотношения:
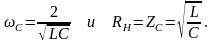
Перемножая эти соотношения, получим:
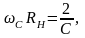 откуда
откуда
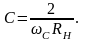
Разделив исходные соотношения, друг на друга, получим:
 откуда
откуда
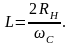
Заметим, что в реальных фильтрах за счет наличия активных сопротивлений в катушках индуктивности и конденсаторах частотные зависимости несколько отличаются от расчетных. Кроме того, различие между расчетными и фактическими соотношениями обуславливается нарушением условия Rн=Zc, которое, как видно из графиков Zc(), делается все более и более несправедливым по мере приближения к граничной частоте.
