4 Динамический расчет системы стабилизации
4.1 Исследование и анализ функциональных свойств системы
4.1.1 Построение временных характеристик по задающему и возмущающему воздействиям
Найдем переходную
характеристику системы по управлению
при задающем ступенчатом воздействии
.
Передаточная функция САС по управлению
имеет вид:
.
Выразим
:
.
Разложим полученное выражение на простые дроби:
.
Для перехода во временную область воспользуемся обратным преобразованием Лапласа:
Г
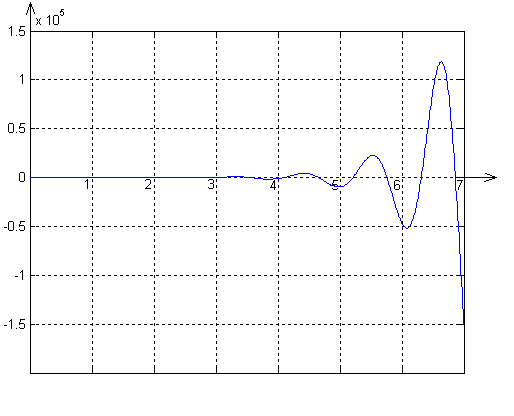
Рисунок 4.1 – Переходная характеристика САС по управлению
Найдем переходную
характеристику системы по возмущению
при моменте сопротивления равном
.
Передаточная функция САС по возмущению
имеет вид:
.
Выразим :
.
Разложим полученное выражение на простые дроби:
.
Для перехода во временную область воспользуемся обратным преобразованием Лапласа:
Г
Рисунок 4.1 – Переходная характеристика САС по возмущению
4.1.2 Построение частотных характеристик
Рассмотрим САС со
стороны управляющего воздействия.
Представим передаточную функцию системы
по управлению в частотной области. Для
этого воспользуемся заменой
:
.
Для того чтобы избавиться от комплексной переменной в знаменателе, умножим числитель и знаменатель на комплексно-сопряженную функцию:
;
.
Амплитудно-частотная и фазо-частотная характеристики системы определяются из зависимостей:
Тогда логарифмическая амплитудно-частотная и фазо-частотная характеристики соответственно имеют вид:
Графики ЛАЧХ и ЛФЧХ представлены на рис. 4.3 и рис. 4.4 соответственно.
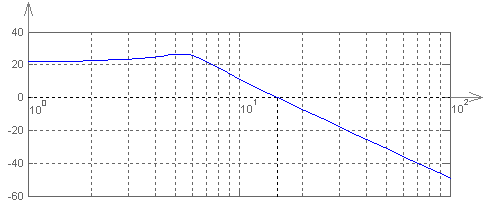
Рисунок 4.3 – График ЛАЧХ
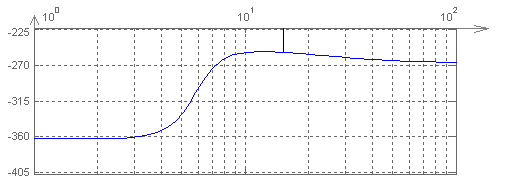
Рисунок 4.4 – График ЛФЧХ
4.1.3 Определение
показателей качества системы (
,
,
σ, М, 
,
,
)
Показатели качества системы представлены в табл.4.1.
Таблица 4.1 – Показатели качества системы
|
, В |
σ, |
М |
,
|
|
, град |
|
|
- |
- |
- |
|
-73,9 |
4.1.4 Анализ управляемости, наблюдаемости и устойчивости исходной системы
Опишем исходную систему в виде пространства состояния. Для этого воспользуемся передаточной функцией САС по управлению:
.
Уравнение вход-выход в изображениях имеет вид:
.
Уравнение вход-выход в оригиналах, решенное относительно старшей производной выходного сигнала имеет вид:
.
Введем следующую переменную состояния:
.
Получим:
Представим систему в векторно-матричной общей форме:
Здесь:
– трехмерный вектор состояния,
– одномерный вектор управления,
– одномерный вектор выхода, A
– матрица динамики, B
– матрица входа, С – матрица выхода, D
– матрица прямой связи.
.
Тогда в развернутой векторно-матричной форме система имеет вид:
.
Понятие управляемости
характеризует возможность перевода
САС посредством допустимого управления
из одного состояния в другое за конечное
время. Необходимым и достаточным условием
управляемости по Калману является:
.
Для исследуемой САС принимаем
.
Получим:
.
Т.к. условие выполняется, значит система полностью управляема.
Понятие наблюдаемости
характеризует возможность непосредственно
или косвенно по выходному вектору САС
определить ее вектор состояния.
Необходимым и достаточным условием
наблюдаемости по Калману является:
.
Для исследуемой САС принимаем
.
Получим:
.
Т.к. условие выполняется, значит система полностью наблюдаема, т.е. все изменения вектора состояния будут отражаться в векторе изменений.
Устойчивость характеризует свойство САС возвращаться в исходное состояние после кратковременного вывода его из этого состояния и прекращения действия возмущения.
Для исследования системы на устойчивость воспользуемся критерием Ляпунова. Необходимым и достаточным условием устойчивости по этому критерию является расположение корней характеристического уравнения линейной математической модели в левой полуплоскости комплексной плоскости корней. Характеристическое уравнение имеет вид:
.
Т.к. комплексно-сопряженные корни имеют положительную действительную часть, т.е. лежат в правой полуплоскости комплексной плоскости, следовательно САС неустойчива.