Vychmat_lektsii / Лекция 11 МКЭ

Лекция 10 13.04.07

Свойства разностных схем для УЧП , аппроксимация , устойчивость и сходимость.

Для разного типа уравнений в частных производных используются разные подходы к построению аппроксимирующей сетки , но можно сформулировать общую схему решения краевых задач математической физики:

Пусть задан некоторый дифференциальный оператор второго порядка ∆u , который является линейным ( ∆(c₁u₁+ c₂u₂)= c₁∆u₁+ c₂∆u₂ ) для любых дважды дифференцируемых функций u_1, u₂ и действительных чисел с₁,и с₂ .

В область определения уравнения ∆u=f вводится прямоугольная вычислительная сетка и аппроксимируется конечно-разностным оператором ∆_hτu .Т.о. справедливо равенство :

∆u=∆_hτu+α_h,τ , где α_h,τ - погрешность аппроксимации. оператора Лапласа

Правило:

Разностная схема удовлетворяет свойству дифференциального оператора , если погрешность α_h,τ стремится к нулю при неограниченном измельчении сетки.

Погрешность приведенных примеров O(h²+τ) или O(h²+τ²) .

В результате исходное дифференциальное уравнение может быть переписано в виде : ∆_hτu(x_i ,y_j)+α_h,τ=f_i,j для узлов сетки.

Тогда с точностью до погрешности можно записать систему алгебраических уравнений ∆_hτu(x_i ,y_j)+α_h,τ=f_i,j относительно приближенного решения.

Теперь рассмотрим критерий устойчивости приближенного решения полученной системы уравнений ( т.е. малые изменения численного решения при малых изменениях правой части уравнения):

Пусть имеем некоторое возмущение правой части системы δf_i,j и ему в ответ было получено соответствующее решение (u_i,j+δu_i,j) :

Вспомнив о линейности оператора и выполнив преобразование , получаем

Свойство устойчивости :

Нормы в конечномерных пространствах , которым принадлежат искомое решение и правая часть , а постоянная c зависит только от коэффициентов оператора ∆_hτu.

Свойства аппроксимации и устойчивости обеспечивают сходимость решения к точному (аппроксимация + устойчивость => сходимость )

Примеры нелинейных уравнений :

• Параболическое

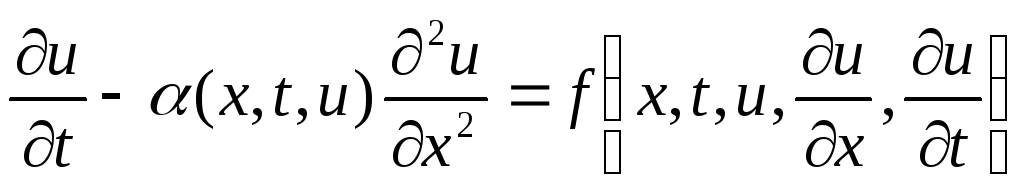
• Гиперболическое

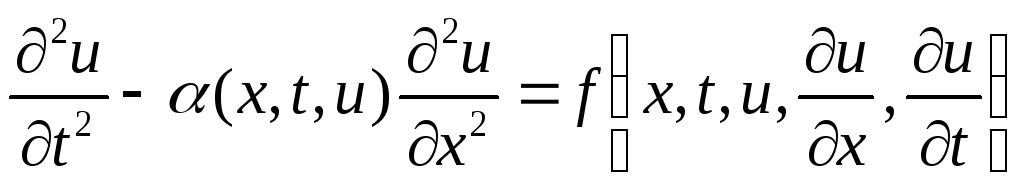
• Э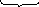ллиптическое

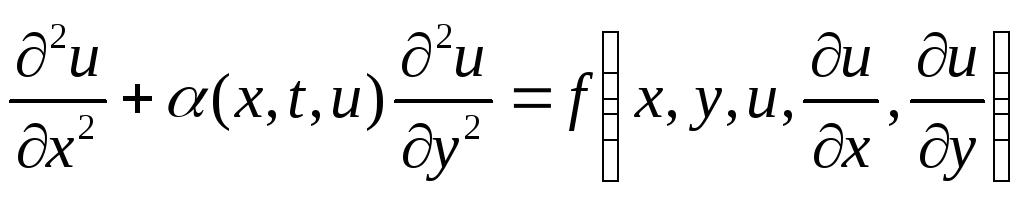
> 0

Важное отличие : возможность возникновения разрывов решений даже при гладких начальных данных.

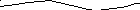
Метод конечных элементов.

В основе метода лежит аппроксимация неизвестной функции, являющейся решением заданного дифференциального уравнения, множеством кусочно-непрерывных функций , определенных на конечном числе подобластей, называемых конечными элементами.

Алгоритм решения задачи :

• Выбираются формы, размеры и расположение подобластей . При этом руководствуются физическими соображениями. Вершины подобластей являются узловыми точками.

• Исследуемую область разбивают на подобласти.

• Выбирается метод аппроксимации каждого элемента( подобласти), т.е. выбирается аппроксимирующая функция

• Определяются физические зависимости между перемещениями , существенные для решаемой задачи

• Получаемая система уравнений решается относительно узловых значений. При необходимости ищутся промежуточные значения искомых функций.

Рассмотрим основные моменты решения плоской задачи теории упругости.

В плоской задаче теории упругости рассматривают два случая – плоское деформированное состояние и плоское напряженное состояние.

Для плоского напряженного состояния компоненты тензора напряжений _z=_zx=_zy=0, компоненты тензора деформаций _yz= _xz=0, а _z величина постоянная. Для плоского деформированного состояния компоненты тензора деформаций _z=_xz=_yz=0, компоненты тензора напряжений _zy=_zx=0, а _z величина постоянная. Конечноэлементное решение для обоих случаев строится одинаково, но с разными матрицами упругих постоянных.

Напряженно-деформированное состояние упругого тела характеризуется вектором деформаций {} и вектором напряжений {} c компонентами

,

где _x,_y – нормальные напряжения по оси X и по оси Y, _xy – касательное напряжение; _x,_y – нормальные деформации по оси X и по оси Y, _xy – деформация сдвига.

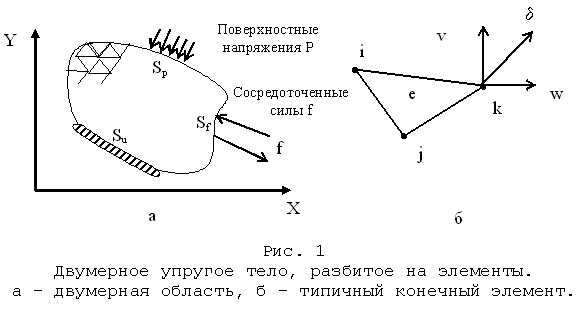
На части границы S_p действуют поверхностные напряжения (распределенная нагрузка), на части границы S_f приложены сосредоточенные силы, а на части границы S_u заданы условия закрепления или известные перемещения. Перемещение каждой точки тела определяется вектором  с горизонтальной компонентой w и вертикальной компонентой V.

Уравнения равновесия без учета объемных сил имеют вид

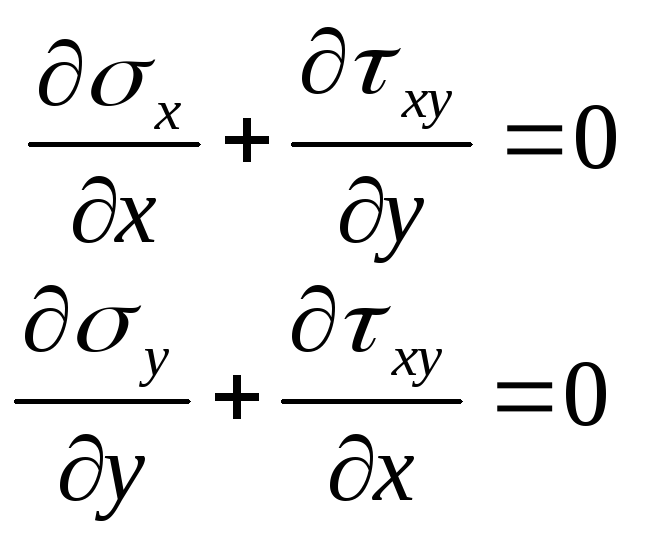
Между деформациями и перемещениями в двумерном случае имеют место соотношения

. (1)

4

стр. из 4