13 Лекция 3 продолжение «Решение слау»

Решение в системе Mahtcad :

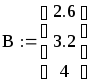
Использование вычислительного блока Given-Find

Сходимость метода Зейделя

Требование критерия сходимости аналогично методу простых итераций.

Существует устойчивое мнение , что метод Зейделя сходится быстрее к точному решению , чем метод простых итераций.

Это действительно только в случае , когда матрица А симметрична и положительно определена.

Дело в том , что эти два метода ориентированы на решение разных классов задач: метод простых итераций- на системы с матрицами, близкими к диагональным, метод Зейделя- на системы с матрицами близкими к нижним треугольным.

7. Численные методы решения нелинейных уравнений и систем. Решение нелинейных уравнений.

Задача отыскания корней нелинейного уравнения решается в два этапа.

Первый – этап локализации ( отделения ) корней

Второй – этап итерационного уточнения корней.

Итерационный метод называется одношаговым, если для вычисления последующего приближения требуется использовать только предыдущее приближение, и к- шаговым , если для вычисления последующего приближения используется к предыдущих приближений в этом случае столько же данных необходимо , чтобы начать метод.

Скорость сходимости метода:

Метод сходимости сходится со скорость геометрической прогрессии , знаменатель которой q<1, если для nN справедлива оценка

.

Для решения нелинейных уравнений также применяется метод Ньютона( касательных) , однако имеются две трудности :

1. вычисления первой производной либо невозможны , либо весьма трудоемки.

2. Л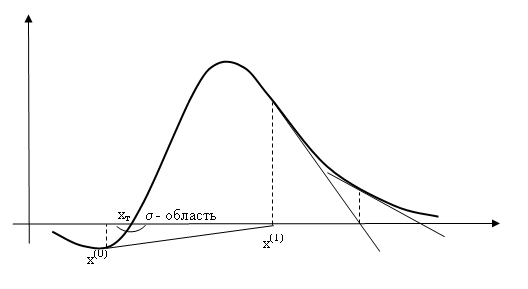окальная сходимость метода. Последовательные приближения могут сходится к точному решению только в малой -окрестности точки x . Неудачный выбор начального приближения может дать расходящуюся последовательность .

Для преодоления этой трудности используют метод Ньютона в сочетании с другим методом , например бисекции.

Метод Ньютона для решения систем нелинейных уравнений.

Пусть дана система n нелинейных уравнений с n неизвестными вида:

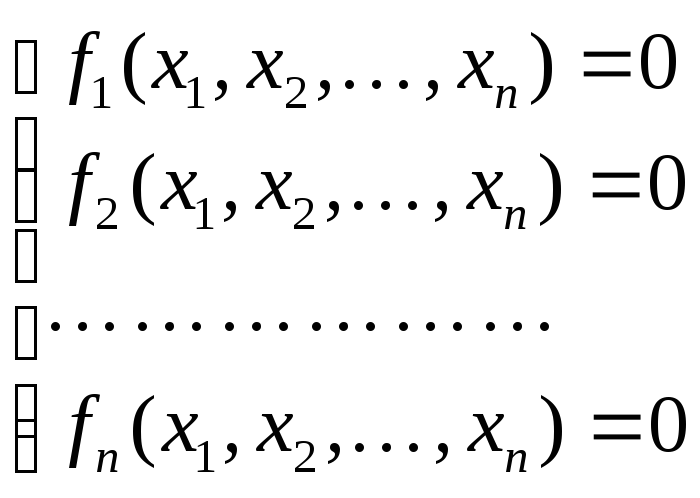
Отыскание решения начинается с локализации корней. Обычно эта задача уже очень сложна , поэтому иногда полное решение локализации невозможно . в простейших случаях помогут графические методы.

В методе Ньютона применяется линеаризация системы.

Пусть по выбранному нулевому приближению построены последующие. Заменим каждую из функций системы уравнений линейной частью ее разложения в ряд Тейлора в точке :

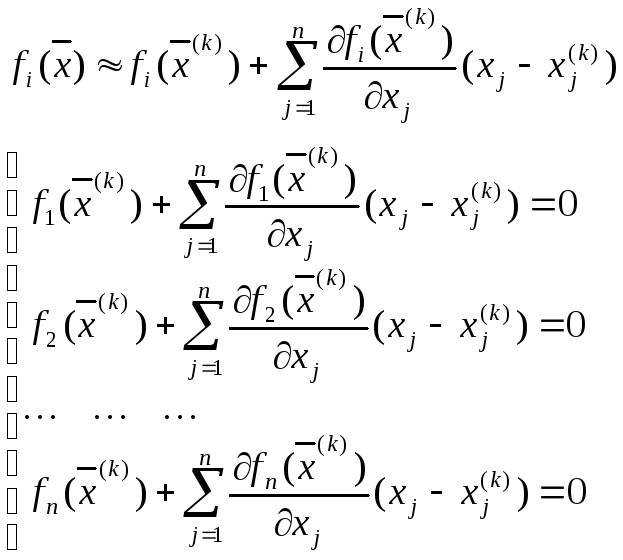
В матричной форме:

где - матрица Якоби

Если матрица невырожденная, т.е. ее определитель det0 , то существует обратная матрица . Тогда существует единственное решение , которое и принимают за очередное приближение к точному решению.

Итерационная формула метода Ньютона для СНЛАУ:

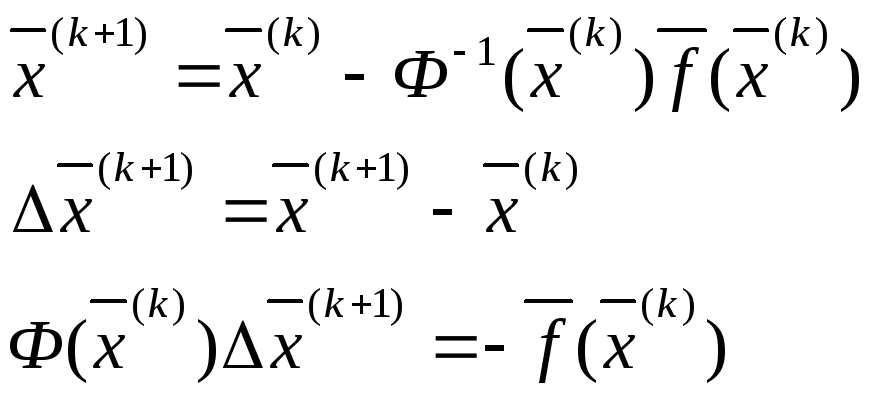
Чаще решается именно нижнее уравнение и затем вычисляется поправка к приближению.

Теоретически условия сходимости метода Ньютона таковы:

1. определитель матрицы Якоби ни в одном цикле не равен нулю;

2. все элементы этой матрицы во всех циклах имеют конечные значения.

На практике из-за погрешностей реализации нужно, чтобы модуль определителя был не слишком мал, а модули элементов не слишком велики.

Акцентируем принципиальный момент: фактически метод Ньютона –это аппроксимация нелинейной системы серией линейных аналогично тому, как нелинейную кривую аппроксимирует серия касательных прямых при решении уравнений с одним неизвестным.

Для систем возможен и модифицированный вариант метода Ньютона. В таком случае во всех циклах используется стартовая матрица Якоби А=.

Тогда имеем:

Это заметно сокращает объём вычислений в каждом цикле, но циклов требуется больше. Сходимость линейная , знаменатель прогрессии тем меньше , чем ближе приближение к точному x .

Баланс этих факторов зависит от свойств конкретных систем: чем сложнее структура элементов , тем обычно эффективнее модифицированный вариант.

Другой вариант метода Ньютона используется при невозможности вычисления производных. Их заменяют конечно-разностными соотношениями, но в этом случае проблемой является выбор шага численного дифференцирования. Этот вопрос мы обсудим в теме ЧД.

Рассмотрим пример:

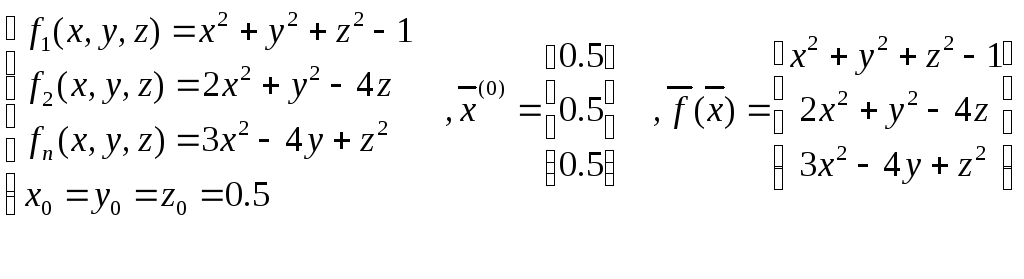
Получим первое приближение

Таблица последовательных приближений :

i	x	y	z
0	0.5	0.5	0.5
1	0.875	0.5	0.375
2	0.78981	0.49662	0.36993
3	0.78521	0.49662	0.36992