Лекция 4

Численные методы решения дифференциальных уравнений.

Дифференциальные уравнения - это уравнения, в которых неизвестными являются не переменные (т. е. числа), а функции одной или нескольких переменных. Эти уравнения включают соотношения между искомыми функциями и их производными.

Определение : Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями (далее чаще используется сокращение ОДУ).

Порядком ДУ называется наивысший порядок производной (или дифференциала), входящей в уравнение.

Степенью ДУ будет та степень , в которой производная наивысшего порядка входит в ОДУ.

ОДУ n – го порядка в общем виде содержит независимую переменную, неизвестную функцию и ее производные (или дифференциалы) до n – го порядка включительно и имеет вид F(x,y,y’,y”,…,y⁽ⁿ⁾)= 0 , где x – независимая переменная, y,y’,y”,…,y⁽ⁿ⁾ – неизвестная функция и ее производные.

ОДУ n – го порядка, разрешенное относительно старшей производной, может быть записано в виде

(1)

Решить (иногда говорят проинтегрировать) дифференциальное уравнение - значит определить неизвестную функцию на определенном интервале изменения ее переменных.

Решением (или интегралом) уравнения (1) называется всякая дифференцируемая функция y = (x) , удовлетворяющая этому уравнению, т.е. такая, после подстановки которой в уравнение (1) оно обращается в тождество.

График решения ОДУ называется интегральной кривой этого уравнения.

Понятно , что решение ОДУ может быть записано в виде

y = (x)+const , (2)

поскольку производная от постоянных равна нулю.

Решение ОДУ, содержащее столько независимых произвольных постоянных, каков его порядок, называется общим решением, которое геометрически представляет семейство интегральных кривых этого уравнения. На рис.1 показано такое семейство интегральных кривых и поле их направлений .

Проекция графика решения ДУ на ось ординат называется фазовой кривой или траекторией ДУ.000000000000000000000000000000000000000000000000000000000000000

Поле направлений , соответствующее ДУ- семейство прямых , тангенс угла наклона которых к оси абсцисс равен f(х,у).

Ч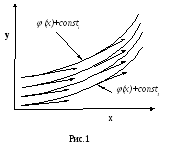астным решением ОДУ называется всякое решение, полученное из общего при определенных значениях произвольных постоянных, входящих в общее решение.

Произвольные постоянные определяются из заранее заданных условий. Условия могут быть начальными или граничными.

Задача с начальными условиями ставится так - найти такое решение (2) уравнения (1), которое должно принимать вместе со своими производными до (n-1) порядка заданные числовые значения y₀, y₀^’ , y₀^” , . . . y₀^(n-1) при заданном числовом значении x=x₀ независимой переменной x:

y=y₀ , y^’=y₀^’ , y^”=y₀^” , . . . y^(n-1)=y₀^(n-1) _. (3)

Условия (3) и называются начальными условиями, числа x₀, y₀, y₀^’ , y₀^” , . . . y₀^(n-1) - начальными данными, а вся задача – задачей с начальными условиями или задачей Коши.

Таким образом, постановка соответствующей задачи Коши для ОДУ первого порядка должна содержать дифференциальное уравнение в стандартной форме (форме Коши):

у' (x)=f (y(x),x) (4)

и одно начальное условие при x=x₀ y(x₀)=y₀ (5)

Требуется определить функцию y(x) на интервале от x₀ до b .

Приближенные методы решение ОДУ можно разделить на две группы:

• аналитические методы, дающие приближенное решение в виде аналитического выражения;

• численные методы, дающие приближенное решение в виде таблицы.

Теорема существования и единственности решения.

Пусть функция f(x,y) определена и непрерывна в области G и удовлетворяет в ней условию Липшица по переменной y , то есть

Тогда для любого начального значения y₀ существует единственное решение y(x) задачи Коши с заданным начальным условием

, определенное на отрезке [x₀,b] .

На практике для дифференцируемых по y функций f(x,y) начальное условие заменяют более грубым условием  f_y (x,y)  с , то есть условием ограниченности частной производной.

Численные методы решения задачи Коши. Основные понятия и определения.

Численное решения задачи Коши строится для ее дискретного аналога . В этом случае отрезок [x₀,b] область непрерывности изменения аргумента x конечным множеством точек x₀< x₁< x₂<… x₀=N , которое называется сеткой . Сетки в большинстве случаев равномерные .

h_n=x_n-x_n-1 - называется шаг сетки. Функции , определенные лишь в узлах сетки , называют сеточными. В общем виде множество узлов обозначают ω^h , а значения функции соответственно f^h .

Часто же значения функции в узлах сетки обозначается обычным способом f(x_n) или f_n.

Суть построения метода лежит в построении замены ДУ

неким дискретным аналогом

- значения функции f(x,y) в соответствующих точках.

Сумма в левой части есть разностная аппроксимация производной y' по одной из формул численного дифференцирования . Функция есть специальным образом построенная аппроксимация функции f(x,y) .

Если при нахождении приближения y_n+1 в очередной точке сетки используется найденные ранее значения сеточной функции в k предыдущих точках сетки , то такой метод называют k – шаговым.

При k=1 имеем

Это одношаговый метод. Вычисление y_n+1 осуществляется с использованием только одного предыдущего значения y_n.

Определение :

В случае , когда входящая в уравнение функция не зависит от y_n+1 , вычисление y_n+1 не вызывает затруднений и осуществляется по явной формуле

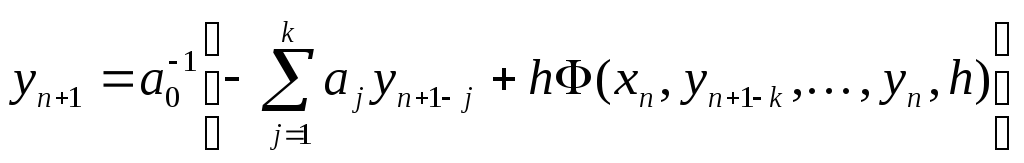
Соответствующий метод называется явным.

Если входящая в уравнение функция зависит от y_n+1 и на каждом шаге приходится решать нелинейное уравнение относительно y_n+1 , метод называют неявным.

Одним из распространенных численных методов решения ОДУ первого порядка с начальными условиями является метод Эйлера .

2.Метод Эйлера.

П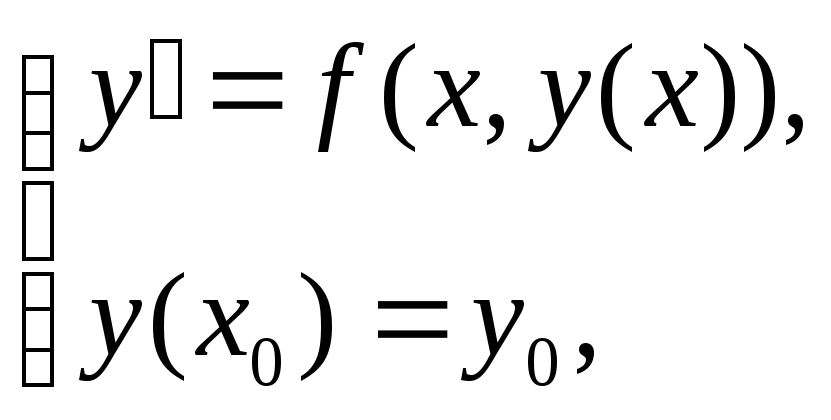усть дано ОДУ первого порядка

с начальным условием

Требуется найти решение на отрезке [a , b] .

Разобьем отрезок [a , b] на n равных частей, получиv последовательность узлов x₀, x₁, . . . , x_n , где x_i = x₀ +ih (i=0,1,…,n), а - шаг интегрирования. Данный способ нахождения приближенного решения для равноотстоящих точек.

Разработано несколько способов вывода формулы Эйлера. Рассмотрим два из них.

2.1. Геометрический способ .

Семейство интегральных кривых ( сплошная и пунктирные линии) представляет общее решение дифференциальн. уравнения.

Точное решение (сплошная линия) в соответствии с начальными условиями проходит через точку А₀ с координатами (x₀,y₀). Заменим точное решение y =(x) касательной к интегральной кривой в точке А₀ при x=x₀ (рис.2).

При x=x₁ получим точку А₁ с ординатой y₁=y₀+htg₀. Но tg₀=y’(x₀) и, учитывая (4), получим y₁=y₀+hf(x₀,y₀), где f(x₀, y₀) - функция, характеризующая наклон касательной в точке А₀. Таким образом, приращение функции заменяем ее дифференциалом. Выполнив аналогичную процедуру в точке А₁, найдем ординату точки А₂ : y₂=y₁+hf(x₁, y₁).

В общем случае для i-ой точки можно записать

y_i+1=y_i+h f(x_i ,y_i ).

Поскольку исходной точкой для каждого прямолинейного отрезка является конечная точка предыдущего, этот метод часто называют методом ломаных. Наклон каждого отрезка ломаной определяется значением производной y’(x_i)=f(x_i,y_i) . Видно , что при выполнении уже первого шага численного решения возникает погрешность вычисления, т.е. ломаная приближенного решения как бы “соскальзывает” с интегральной кривой точного решения.

2.2. Способ с использованием ряда Тейлора

Разложим искомую функцию в ряд Тейлора в окрестности начальной точки x₀ :

.

При x=x₁ получим .

Переписав его в виде: y₁=y₀+h f(x₀, y₀)+R(h),

придем к формуле Эйлера, но уже с остаточным членом

, где (x₀,x₁) .

Остаточный член характеризует локальную (шаговую) ошибку, которая для метода Эйлера имеет второй порядок O(h²) . Глобальная (суммарная) ошибка в конце отрезка [a, b] будет, очевидно, равна n О(h²), но учитывая, что , получим погрешность О(h), т.е. метод Эйлера имеет первый порядок точности и в этом состоит его основной недостаток.

3. Первый модифицированный метод Эйлера

С целью повышения точности разработано несколько модификаций метода Эйлера. Рассмотрим сначала одну из них – первый улучшенный метод ломаных.

Сначала на каждом i -ом шаге, как и в методе Эйлера, используя наклон касательной в точке A_i (х= x_i), вычисляют промежуточное значение y_i+1/2 , но не на всей длине шага h , а на его половине в средней точке A_c (х=x_i+1/2 ) каждого интервала [x_i , x_i+1] (Рис.3.):

Затем находят направление касательной f_i+1/2 в середине интервала в точке A_c (х=x_i+1/2=x_i+h/2) :

Это направление и принимают за окончательное при вычислении ординаты точки A_i+1 на всем интервале h от точки A_i:

Подставив в последнюю формулу два предыдущих выражения, получим одну результирующую формулу для вычисления ординаты точки A_i+1:

На рис.3 точка E при х= x_i+1 была бы получена методом Эйлера, в этом методе будет получена точка A_i+1.