Vychmat_lektsii / Лекция 6 Метод Зейделя

11

Лекция 6 продолжение «Решение СЛАУ»

Замечание к предыдущей теме:

Для установления момента прекращения итераций при достижении заданной точности может быть использована формула:

Алгоритм решения системы методом итерации реализуется так:

1. Приведение системы Ax=B к виду с преобладающими диагональными коэффициентами.

2. Разделить каждое уравнение на соответствующий диагональный коэффициент x=B+Ax .

3. Проверить выполнение условий для какой-либо из норм приведенной матрицы

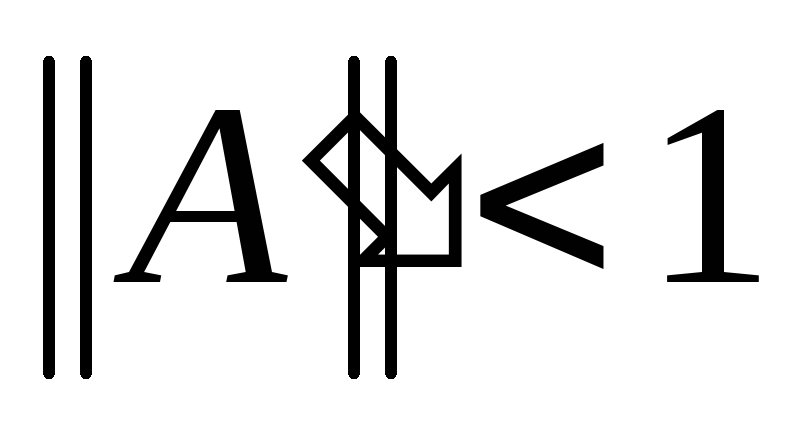
4. Реализовать итерационный процесс ( рекомендуется в качестве начального приближения выбрать столбец В ).

Метод Зейделя

Отличие метода Зейделя от метода простых итераций заключается в том, что при вычислении (k+1)-го приближения неизвестного x_i учитываются уже вычисленные ранее (k+1)-ые приближения неизвестных x₁ ,x₂ ,…,x_i-1.

Таким образом, предполагая, что k-е приближение корней известны, (k+1)-ые приближения вычисляют по следующим формулам:

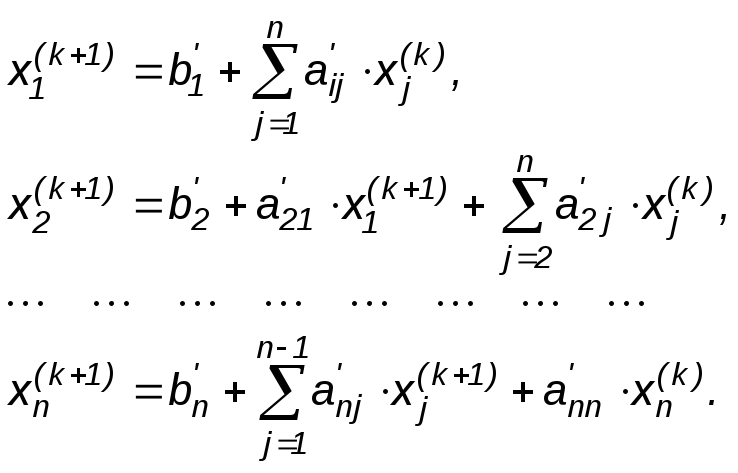где (k=0,1, … ,n).

Рассмотрим пример решения методом простых итераций и методом Зейделя:

Первоначальный ход одинаков :

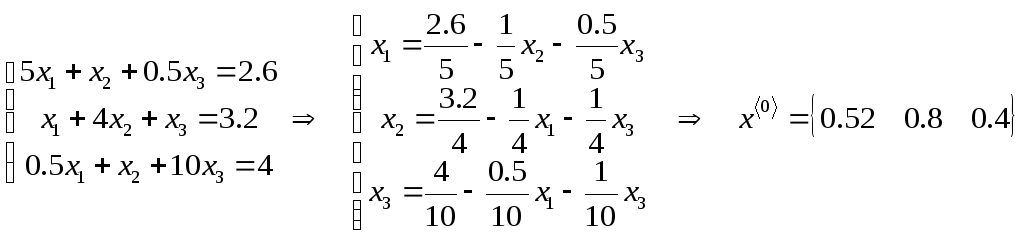
Далее начинаются различия:

а) для метода простых итераций

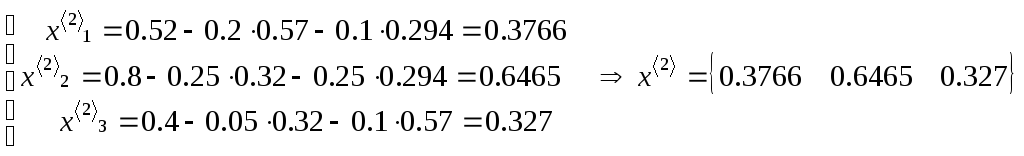
в) для метода Зейделя

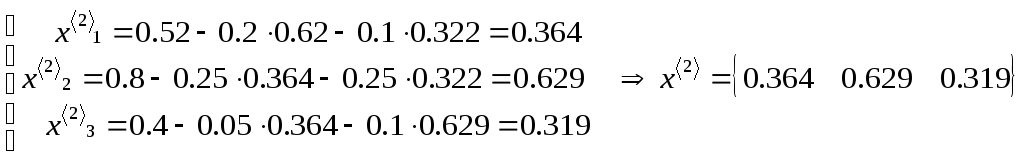
Решение в системе Mahtcad :

Использование вычислительного блока Given-Find

Сходимость метода Зейделя

Требование критерия сходимости аналогично методу простых итераций.

Существует устойчивое мнение , что метод Зейделя сходится быстрее к точному решению , чем метод простых итераций.

Это действительно только в случае , когда матрица А симметрична и положительно определена.

Дело в том , что эти два метода ориентированы на решение разных классов задач: метод простых итераций- на системы с матрицами, близкими к диагональным, метод Зейделя- на системы с матрицами близкими к нижним треугольным.

7. Численные методы решения нелинейных уравнений и систем.

Решение нелинейных уравнений.

Задача отыскания корней нелинейного уравнения решается в два этапа.

Первый – этап локализации ( отделения ) корней

Второй – этап итерационного уточнения корней.

Итерационный метод называется одношаговым, если для вычисления последующего приближения требуется использовать только предыдущее приближение, и к- шаговым , если для вычисления последующего приближения используется к предыдущих приближений в этом случае столько же данных необходимо , чтобы начать метод.

Скорость сходимости метода:

Метод сходимости сходится со скорость геометрической прогрессии , знаменатель которой q<1, если для nN справедлива оценка

.

Для решения нелинейных уравнений также применяется метод Ньютона( касательных) , однако имеются две трудности :

1. вычисления первой производной либо невозможны , либо весьма трудоемки.

2. Локальная сходимость метода. Последовательные приближения могут сходится к точному решению только в малой -окрестности точки x . Неудачный выбор начального приближения может дать расходящуюся последовательность .

Для преодоления этой трудности используют метод Ньютона в сочетании с другим методом , например бисекции.

Метод Ньютона для решения систем нелинейных уравнений.

Пусть дана система n нелинейных уравнений с n неизвестными вида:

Отыскание решения начинается с локализации корней. Обычно эта задача уже очень сложна , поэтому иногда полное решение локализации невозможно . в простейших случаях помогут графические методы.

В методе Ньютона применяется линеаризация системы.

Пусть по выбранному нулевому приближению построены последующие. Заменим каждую из функций системы уравнений линейной частью ее разложения в ряд Тейлора в точке :

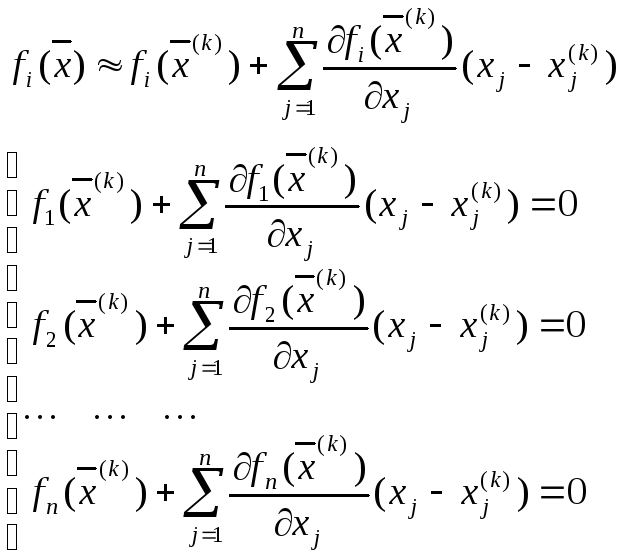
В матричной форме:

где - матрица Якоби

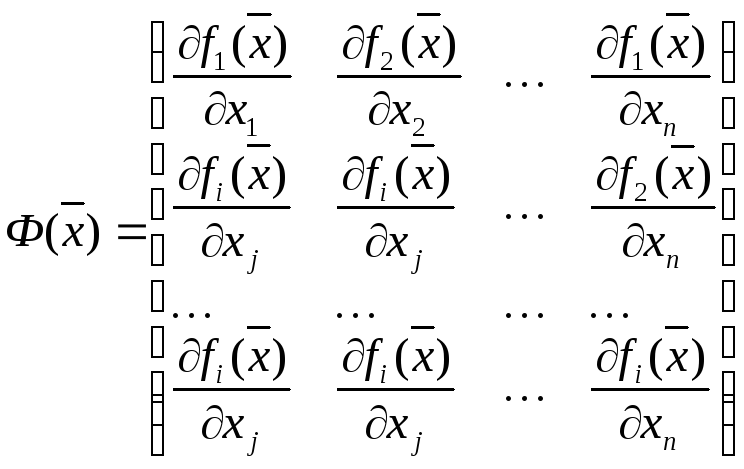
Если матрица невырожденная, т.е. ее определитель det0 , то существует обратная матрица . Тогда существует единственное решение , которое и принимают за очередное приближение к точному решению.

Итерационная формула метода Ньютона для СНЛАУ:

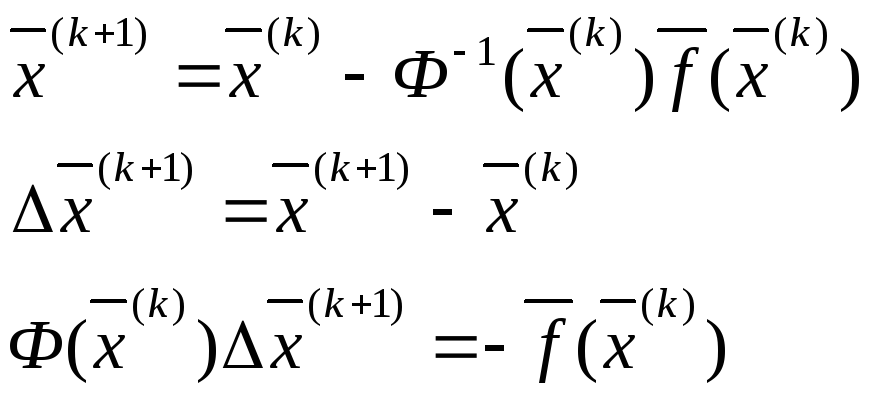
Чаще решается именно нижнее уравнение и затем вычисляется поправка к приближению.

Теоретически условия сходимости метода Ньютона таковы:

1. определитель матрицы Якоби ни в одном цикле не равен нулю;

2. все элементы этой матрицы во всех циклах имеют конечные значения.

На практике из-за погрешностей реализации нужно, чтобы модуль определителя был не слишком мал, а модули элементов не слишком велики.

Акцентируем принципиальный момент: фактически метод Ньютона –это аппроксимация нелинейной системы серией линейных аналогично тому, как нелинейную кривую аппроксимирует серия касательных прямых при решении уравнений с одним неизвестным.

Для систем возможен и модифицированный вариант метода Ньютона. В таком случае во всех циклах используется стартовая матрица Якоби А=.

Тогда имеем:

Это заметно сокращает объём вычислений в каждом цикле, но циклов требуется больше. Сходимость линейная , знаменатель прогрессии тем меньше , чем ближе приближение к точному x .

Баланс этих факторов зависит от свойств конкретных систем: чем сложнее структура элементов , тем обычно эффективнее модифицированный вариант.

Другой вариант метода Ньютона используется при невозможности вычисления производных. Их заменяют конечно-разностными соотношениями, но в этом случае проблемой является выбор шага численного дифференцирования. Этот вопрос мы обсудим в теме ЧД.

Рассмотрим пример:

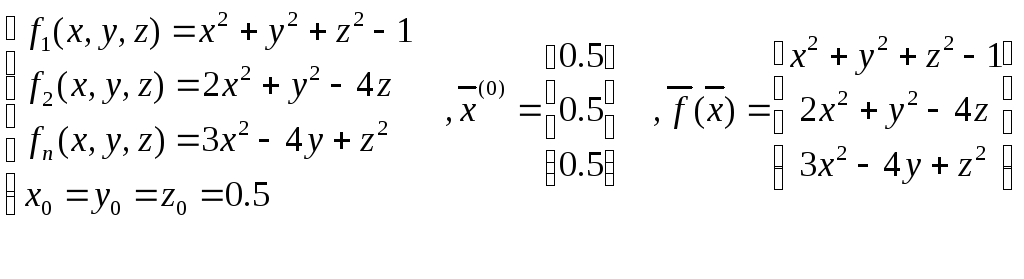
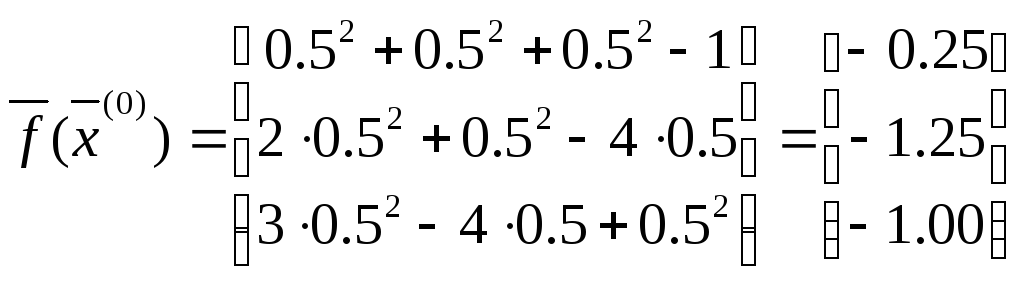
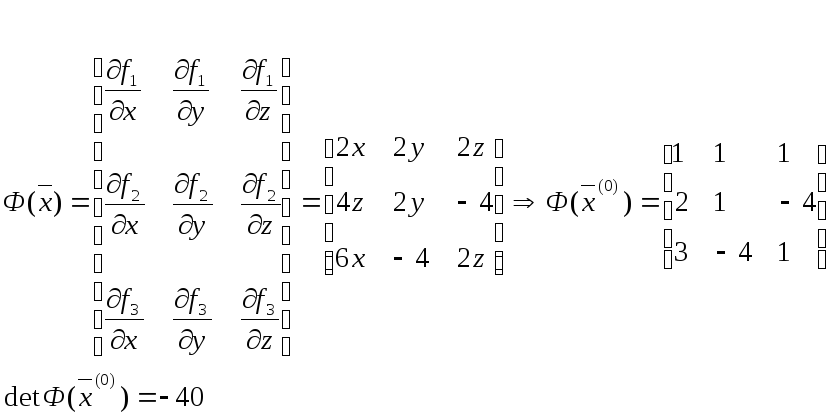
Получим первое приближение

Таблица последовательных приближений :

i	x	y	z
0	0.5	0.5	0.5
1	0.875	0.5	0.375
2	0.78981	0.49662	0.36993
3	0.78521	0.49662	0.36992

Метод простой итерации

Базовое уравнение f(x)= по аналогии со скалярным вариантом приводится к эквивалентной векторной форме

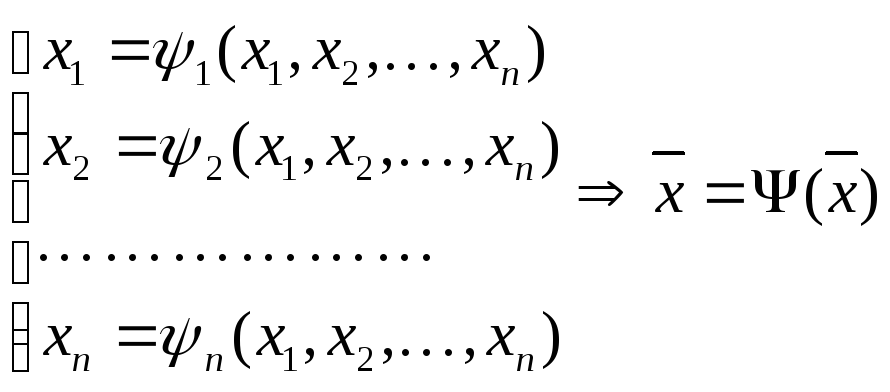
и организуется процесс

Если выполняются определённые условия, то предел x_ создаваемой последовательности при k совпадает с искомым вектором x*.

У вектор-функции (x) также есть матрица Якоби со структурой (x), но вместо частных производных функций f_n(x₁, x_2,…x_n) матрица(x) будет состоять из частных производных функций _n(x₁, x₂,…x_n).

Условие сходимости простой итерации определяется именно через матрицу Якоби (x), и формально определяется так:

в каждом столбце или в каждой строке (x), модуль диагонального элемента больше суммы модулей остальных элементов этого столбца или этой строки.

Подчеркнём, что это относится ко всем циклам итерации, так как по мере развития процесса значения частных производных изменяются.

В данном случае также может быть применим метод Зейделя и его многомерный аналог называется методом покоординатных итераций.

Критерии завершения процесса те же, что и для метода Ньютона.

Потоковая технология задания нулевых приближений

Успех итерационного решения существенно зависит от удачного выбора нулевых приближений. Аналитические методы редко позволяют это сделать. За счет определённых дополнительных компьютерных вычислений можно во многих случаях получить соответствующую информацию. Для этого нужно создать такой искусственный параметризованный поток вариантов задачи, что для одного элемента этого потока выбор нулевого приближения прост, а для других элементов он определяется по принципу «новый результат как функция предыдущего». Поток может быть естественным, если в задаче имеется подходящий параметр, или искусственным.

Поясним это на примере уравнения с одним неизвестным.

Пусть требуется решить методом простой итерации уравнение e^-x–x=0, не имеющее аналитического решения. Используем форму x= e^-x; на рисунке

y

x+0.8

Рисунок

это пересечение нижней прямой y=x с экспонентой. Введём в задачу искусственный параметр : x+= e^-x. Очевидно, при =0 новое параметризованное уравнение будет совпадать с первоначальным. Теперь присвоим  значение 1. Это пересечение верхней прямой y=x+1 с экспонентой Видно, что корень нового уравнения x*(=1)=0. Теперь пусть =0.8. Прямая y=x+0.8 линия опустилась, корень уравнения x(=0,8) сместится вправо. Вычисление этого корня проведём при нулевом приближении x₀=x*(=1) Близость x₀ к искомому результату позволит быстро решить уравнение. В данном случае x*(0.8)= 0.103 . Снова уменьшим  на 0.2. Корень х(=0.6) будем вычислять уже при нулевом приближении x₀= 0.103 и получим x*(0.6)= 0.210.

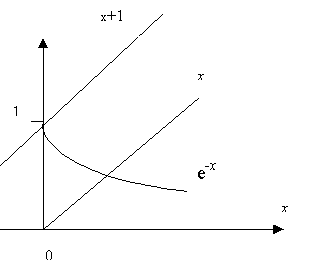
Раз за разом уменьшая , получим x*(0.4)= 0.324, x*(0.2)=0.424 и, наконец, вернёмся при =0 к первоначальному уравнению, и при нулевом приближении x₀=0.424 получим результат x*=x*(0) =0.567.

Чем меньше шаг изменения параметра, тем надежнее будет процесс и быстрее будут сходиться итерации на каждом уровне, но, разумеется, при большем количестве уровней.

Баланс суммарного количества операций зависит от вида уравнения, но фактор надёжности может доминировать и при балансовой выгоде крупного шага.

Принципиальное условие применимости процесса – непрерывность решения по параметру , что в большинстве случаев можно обеспечить.

11