Лекция 12

Задачи оптимизации

Явно или неявно задачи оптимизации возникают постоянно в любой сфере деятельности. Экономическое планирование , управление, распределение ограниченных ресурсов , анализ производственных процессов, проектирование сложных объектов всегда связано с поиском наилучшего варианта.

НО ! Прежде чем воспользоваться математическим аппаратом , надо сформулировать проблему как математическую задачу , и математически записать смысл оценок «хуже» и «лучше».

Численная оптимизация – поиск наилучшего варианта управляемых параметров с точки зрения некоторого критерия.

Многие задачи оптимизации сводятся к отысканию экстремального значения некоторой функции , которую принято называть целевой функцией.

Постановка задачи и методы исследования зависят от свойств целевой функции. Если функция задается явной формулой и при этом дифференцируема, то это наиболее простой , в математической понимании , случай. Продифференцировав такую функцию , можно найти точки ее локальных экстремумов, направления возрастания и убывания .

Однако если функция получена в результате эксперимента или она не может быть задана формулой , задача исследования становится значительно сложнее , тем более если имеем дело с несколькими аргументами.

Далее рассмотрим решение одномерных и менее подробно многомерных задач оптимизации

• Одномерные задачи наиболее просты , на них легче понять постановку вопроса , методы решения и возникающие трудности

• В ряде случаев одномерные задачи имеют самостоятельный интерес

• Алгоритм решения многомерных задач часто можно свести к последовательному многократному решению одномерных задач

Самый простой пример задачи оптимизации:

Задача о консервной банке.

Указать наилучший вариант консервной банки фиксированного объема V , имеющей форму простого кругового цилиндра.

Вопрос: По какому признаку банка считается лучшей ?

Могут быть два варианта:

1. Наименьшая поверхность ( расход жести)

2. Наименьшая длина ( сварной шов )

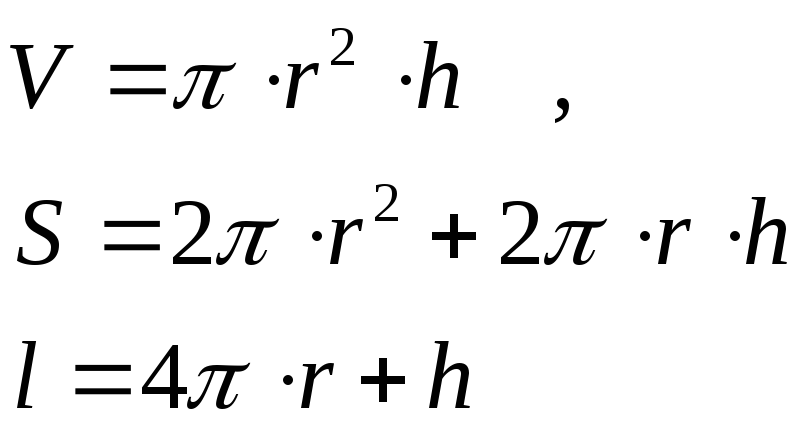
Таким образом надо исследовать полученные функции на минимум .

В соответствии с правилом поиска точек экстремума функции надо вычислить производную и прировнять ее к нулю , а потом рассмотреть полученные промежутки аргумента.

Имеем:

для оптимизации по варианту 1:

Получаем решение или ( подставляя в h )

Тогда оптимальная поверхность будет

Для оптимизации по варианту 2:

или

Видно , что при изменении самой постановки критерия оптимизации решение задачи различно.

Таким образом всегда существуют стратегия и тактика вычислительной оптимизации.

Тактика -выбор конкретного варианта при выполнении определенных этапов решения.

Стратегия – выбор принципа поиска оптимизации.

Одномерные задачи оптимизации

Постановка задачи :

Найти наименьшее ( или наибольшее) значение целевой функции f , заданной на множестве D, принадлежащем арифметическому множеству чисел Rⁿ .

Точки множества D называют допустимыми точками, D –допустимое множество, f - целевая функция задачи.

Определение:

Точка называется глобальным решением задачи , если

И точка есть локальное решение задачи , если найдется окрестность U точки , в которой .

Точки экстремума еще называют стационарными.

Понятно , что всякое глобальное решение будет локальным, но не всегда наоборот. Всякую задачу максимизации можно заменить эквивалентной задачей минимизации.

Известно , что в математическом анализе теорема Вейерштрасса ( о существовании для функции , определенной и непрерывной на некотором промежутке , экстремальных значений ) в данном случае играет роль теоремы существования – решение будет всегда. Однако при не замкнутом пространстве применение теоремы невозможно.

А вот методы , которыми осуществляется поиск этих экстремумов , могут быть различными. Будем рассматривать наиболее простой класс задач ( аналог задаче о консервной банке). Полагаем, что целевая функция дифференцируема на промежутке и есть возможность найти явное выражение для ее производной.

Скорость изменения функции в стационарных точках равна нулю.

Правило решения оптимизации для рассматриваемого класса функций:

На заданном промежутке осуществить поиск стационарных точек , вычислить в них значения самой функции , определить значения функции в граничных точках и сравнивая полученные величины определить наименьшее и наибольшее значение функции . В самом идеальном и простом случае , решение можно найти аналитически , но в реальной жизни может вообще не существовать никакой формулы для целевой функции, только знаем ее значения для любой из точек заданного промежутка ( в результате эксперимента).

Значит решать надо численно.

Определяя значения непрерывной функции f(x) в некотором конечном числе точек заданного отрезка [a,b] , нужно приближенно найти наименьшее ( наибольшее) значение на данном отрезке.

Чаще всего допустимое множество задачи задается в следующем виде:

P – прямые ограничения, F,G –функциональные ограничения .Такое деление весьма условно и в каждом конкретном случае решается исходя из условий задачи.