Vychmat_lektsii / Лекция 9 УЧП

8

Лекция 8

Краевые задачи для обыкновенных дифференциальных уравнений.

Пусть дано ДУ вида

или Найти функцию y=y(x) , которая внутри отрезка [a,b] удовлетворяет дифференциальному уравнению , а на концах отрезка - краевым условиям

Ограничимся рассмотрением линейной краевой задачей для одного уравнения , т.е. дифференциальное уравнение и граничные условия линейные.

Тогда имеем систему:

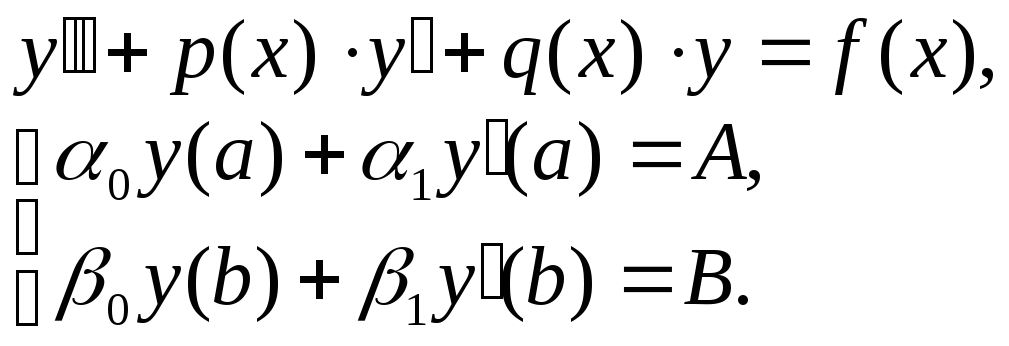
Здесь - известные непрерывные на [a,b] функции, заданные постоянные , причем │α₀│+│α₁│≠0 и │β₀│+│β₁│≠0 .

Определение : Краевые условия называются однородными , если A=B=0

Методы приближенного решения краевых задач :

• Разностные методы

• Аналитические методы

Метод конечных разностей для решения линейных дифференциальных уравнений II порядка.

Решение линейной краевой задачи будем отыскивать на равномерной сетке .

Пусть x₀=a , x_n=b, x_i=x₀+i·h , p_i=p(x_i), q_i=q(x_i), f_i=f(x_i) .

Приближенные значения функции y(x) и ее производных , которые будем получать в результате вычислений в узлах сетки x_i будут иметь соответственно индексы i .

Согласно формулам численного дифференцирования заменим величины производных через соотношения конечных разностей:

, и согласно граничным условиям

Можно заметить , что здесь мы пользуемся формулой для правых разностей .

Тогда получаем систему уравнений :

Это система линейных алгебраических (n+1) уравнений с (n+1) неизвестными. Решив такую систему , получим таблицу искомых приближенных значений функции ( если система разрешима ).

Понятно , что более точные формулы можно получить , если использовать центрально-разностные соотношения :

Соответственно , система будет иметь вид ( обратите внимание на i ):

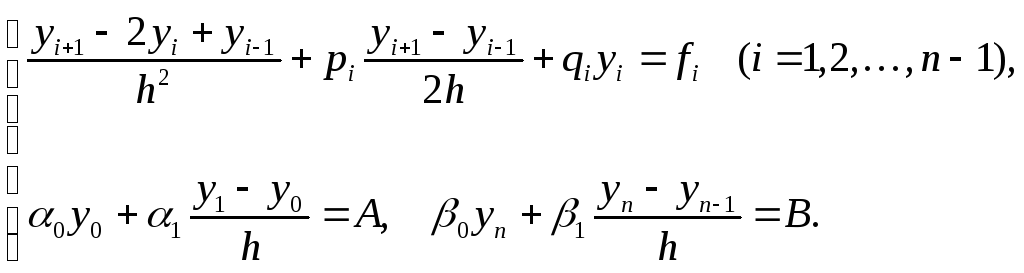
Конечно , надо понимать , что при большом n решение системы будет громоздкое.

Аппроксимация производных конечными разностями вводит методическую погрешность , которую можно оценить :

Чем больше размер системы , тем выше погрешность реализации .

Если исходное уравнение было нелинейным , то получим в результате систему нелинейных уравнений.

Точность разностного метода может быть повышена ,если при выполнении такой замены использовать многоточечные разностные схемы .

Рассмотрим пример :

Методом конечных разностей найти решение краевой задачи :

Заменяем и получаем:

Приведя подобные , имеем :

Пусть шаг h будет 0,1. Тогда получаем три внутренних узла x_i=x₀+i∙h=1+0.1∙i (i=1,2,3).

Д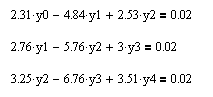ля этих узлов получаем систему уравнений :

C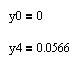 граничными условиями :

Р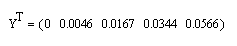ешение системы :

Точное решение данной краевой задачи . Можно проверить , что получили расхождение только в двух узлах ( 0,0047 и 0,0166 ) .

Метод прогонки .

Как уже было замечено при больших n система уравнений , полученных в результате использования конечно-разностных соотношений, становится громоздкой .

Специально для решения такого вида систем был разработан метод прогонки . Имеем :

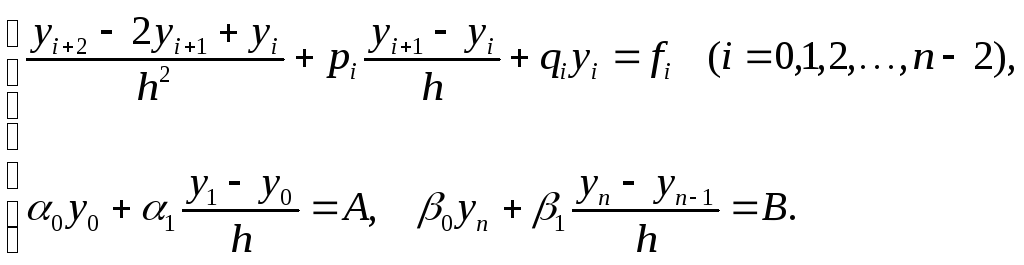
Произведем замены слагаемых для первых (n-1) уравнений в следующем порядке:

Тогда система приводится к виду :

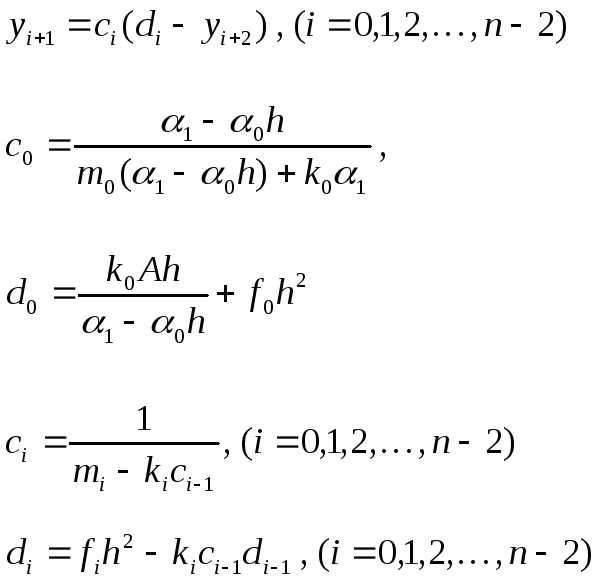
Вычисления проводятся прямым и обратным ходами.

Прямой ход: Сначала вычисляют m_i,k_i, →c₀, d₀→c_i,d_i.

Здесь происходит заготовка вспомогательных чисел , при вычислении нулевых значений используется краевое условие на левом отрезке интегрирования.

Обратный ход :

На первом шаге происходит согласование полученных чисел с краевым условием на правом конце отрезка интегрирования , после чего последовательно получаются значения искомой функции y_i в порядке убывания индекса.

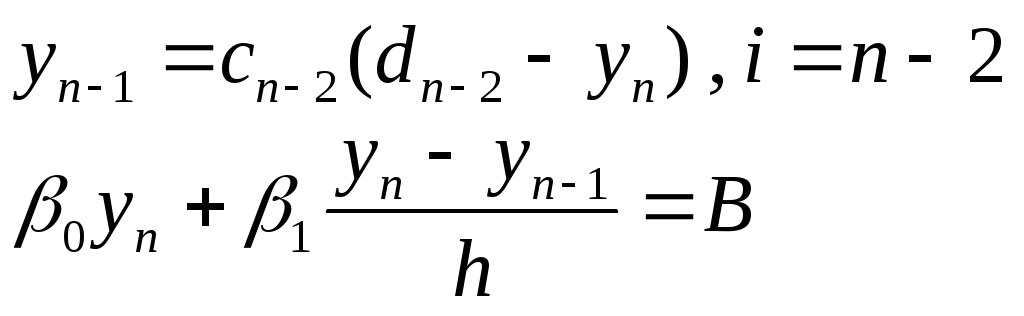
Тогда находим :

Теперь последовательно вычисляем y_i для i=n-1,…,2,1.

И заключительное вычисление :

Подробные примеры выполнения вычислений можно найти в учебнике Н.В.Копченова , И.А. Марон «Вычислительная Математика в примерах и задачах» Метод конечных разностей также применяется для решения нелинейных дифференциальных уравнений II порядка. Конечно , формулы расчета при этом изменяются.

Существуют также и аналитические методы , дающие возможность найти приближенное решение линейной краевой задачи .

Среди таких методов можно указать метод Галеркина и метод коллокаций .

Численные методы решения дифференциальных уравнений в частных производных.

Большое количество сложных физических процессов гидродинамики, теории поля , электродинамики , физической кинетики , статистической физики , квантовой механики и других разделов физики описываются уравнениями в частных производных . Методы численного решения этих уравнений являются наиболее сложной и важной областью вычислительной математики, которая опирается на методы всех остальных областей. Вследствие большого разнообразия задач и численных методов решения этих задач , существующего стандартного программного обеспечения часто бывает недостаточно и требуется дополнительно разрабатывать программы решения конкретной задачи.

Уравнения в частных производных - УЧП.

Определение :

Уравнение относительно неизвестной функции u(x,y) двух или более независимых переменных , которое содержит частные производные этой функции, называется УЧП.

Основное внимание будет уделено УЧП второго порядка.

В общем виде ДУ второго порядка относительно функции двух независимых переменных u(x,y) записывается так :

Функция F- заданная функция восьми аргументов .

Далее будем рассматривать линейные уравнения второго порядка :

Все коэффициенты и правая часть не зависят от u(x,y).

Методы классификации УЧП :

• По порядку уравнения ( наивысший порядок частных производных, входящих в уравнение)

• По числу переменных ( по числу независимых переменных )

• По критерию « линейное-нелинейное»

A,B,C,D,E,F,G – константы или заданные функции переменных x,y.

• По критерию «однородное-неоднородное»

Однородное , если G(x,y)≡0 для всех x и y.

Если G(x,y)≠0 – неоднородное .

• По виду коэффициентов

A,B,C,D,E,F,G – константы – уравнение с постоянными коэффициентами.

Основные типы УЧП :

• Параболический тип :

Описывает процессы теплопроводности и диффузии : B²=4AC

• Гиперболический тип

Описывает колебательные системы и волновые движения : B²>4AC

• Эллиптический тип

Описывает установившиеся процессы : B²<4AC

Введем понятие оператора :

Примеры УЧП :

Название	Формула	Пример физ. процесса
Уравнение Лапласа	∆u=0	Установившиеся процессы
Уравнение Пуассона		Теплопередача с внутренними источниками энергии
Уравнение диффузии		Нестационарная теплопроводность
Волновое уравнение		Распространение волн
Бигармоническое уравнение		Процессы деформации пластин под влиянием внешних сил

Пример :

y>0 – эллиптическое

y=0 – параболическое

y<0 – гиперболическое

Методы решения УЧП:

разделение переменных

• интегральные преобразования

• преобразование координат

• преобразование независимой переменной

численные методы

• метод теории возмущений

• метод функции Грина

• метод интегральных уравнений

вариационные методы

• метод разложения по собственным функциям

• метод обратной задачи рассеивания

8

стр. из 8