14

Лекция 2 продолжение «Теория погрешностей»

В) Погрешность вычитания

Абсолютная погрешность

Относительная погрешность

Обсудим операцию вычитания при близких значениях операндов, имеющих большие абсолютные погрешности. Относительная погрешность из-за деления на очень малый знаменатель может оказаться недопустимо большой. Рекомендуется по возможности избегать вычитания близких чисел.

При обработке нескольких операндов погрешности аддитивных операций можно вычислять по указанным выше правилам. Но при большом количестве операндов получаемые таким способом предельные оценки чрезмерно завышаются. Обычно в этих случаях используют вероятностные оценки.

С

Можно не учитывать

) Погрешность умножения

Абсолютная погрешность

Относительная погрешность

Видно, что здесь опасны деления больших по модулю чисел на значительно меньшие из-за роста абсолютной погрешности.

D) Погрешность деления чисел:

Абсолютная погрешность

Относительная погрешность

E) Погрешность функции

Абсолютная погрешность

Относительная погрешность

Здесь особо опасны быстро меняющиеся функции.

Баланс внутренних погрешностей. Рассмотрим простейшую задачу вычисления суммы членов бесконечного сходящегося ряда

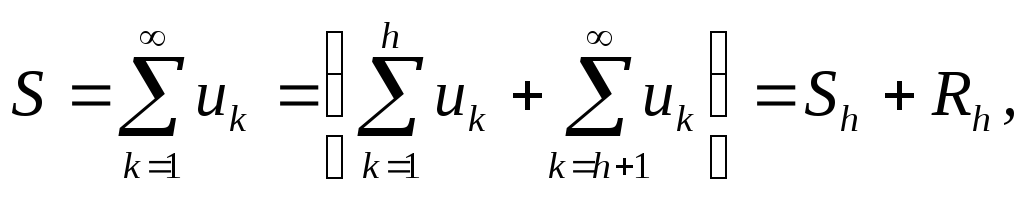
где S_h – это частичная сумма ряда, R_h – остаток. Сходимость ряда означает, что R_h  0 при h  ∞, поэтому при достаточно большом h принимают S  S_h с абсолютной методической погрешностью _метS= R_h.

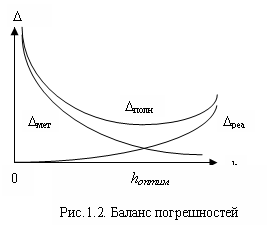
Чем больше членов в сумме S_h, тем меньше эта составляющая полной погрешности. Другая составляющая – это суммарная погрешность реализации _реаS вычисления удерживаемых членов ряда и их сложения.

Ясно, что она растёт по мере удлинения части S_h. Качественная картина баланса погрешностей этого процесса приведена на рис.1.2.

Верные знаки.

Определение

Говорят, что n первых чисел приближенного числа являются верными , если абсолютная погрешность этого числа не превышает 5 единиц разряда, который следует за этим знаком.

Например, с точностью до 10^-9 число =3.141592654. Есть простое правило приближенного вычисления: 22/7= 3.142857143 (также с точностью 10^-9). Абсолютная погрешность здесь 0.001264489.

Следовательно, верными являются только три знака: 3.14;

знак 2 на четвертой позиции уже неверен, так как погрешность 0.0013 больше допустимого для этого знака барьера 0.0005.

Не рекомендуется сохранять неверные знаки при использовании данных, особенно при выдаче результатов.

2.4.Уровни точности.

1. Заказанная точность

2. Потенциально достижимая точность

3. Реально достижимая точность.

Заказанную точность определяют инициаторы постановки задачи как желательную или необходимую для достижения конечных целей. Эти цели обычно предполагают принятие некоторых решений человеком или ЭВМ. Точный ответ ведёт к принятию лучшего решения, приближенный (неточный) — не к лучшему. Эти решения инициируют последствия, различие которых и является конечным мерилом точности. Это особенно важно при постановке неустойчивых задач с порогами принятия решений.

Потенциально достижимая точность зависит от свойств используемой математико-логической модели и от точности её числовых параметров.

Реально достигаемая точность оказывается меньшей из-за искажающих факторов компьютерной реализации. Она может маскироваться значностью ответов, выдаваемых ЭВМ. Не исключено, что даже самый старший разряд не будет верным. Лишние показанные знаки создают иллюзию хорошей точности даже там, где она очень плохая; количество же показанных знаков может быть заданно пользователем почти произвольно.

Если заказанная точность недосягаема, остаётся хотя бы приблизить реально достигаемую точность к потенциально достижимой.

2.5 Точность определения аргумента для функции , заданной таблицей.

В вычислительной практике часто возникает необходимость определить аргумент по значению функции , заданной таблицей.

Понятно , что при этом погрешность в определении функции вызывает погрешность в определении аргумента .

Пусть имеем таблицу с одним входом для функции y=f(x).

Если функция f(x) дифференцируема , то для достаточно малых значений х имеем :

Отсюда или

2.6. Пространства объектов. Типы вычисляемых объектов.

Простейшие вычисляемые математические объекты – это скаляры. Вычисляются также комплексные числа, функции одного или нескольких аргументов, структурированные объекты – упорядоченные наборы скаляров (векторы и матрицы) и функций (вектор-функции) и еще более сложные объекты. Для вычисления объектов разных типов используются свои методы.

Важно иметь достаточно общие математические средства для описания и анализа объектов и численных методов. Такие средства являются предметом функционального анализа - сравнительно новой математической науки. Она трактует математические объекты как элементы некоторых общностей — пространств. Одним элементам могут ставиться в соответствие другие; при этом должны быть определены процедуры установления соответствия, которые называют операторами.

Понятие пространства тесно связано с вопросами точности.

Пространство – это совокупность однотипных объектов, в которой

• объекты отличимы друг от друга;

• установлена структура, т.е. формальные соотношения между элементами:

• выполнение простейших операций над элементами (линейность),

• измерение расстояния между элементами (метричность),

• измерение величины элемента (нормированность).

Принадлежность элемента Z или нескольких элементов Z₁, Z₂, Z₃ пространству Q обозначают ZQ или Z₁, Z₂, Z₃Q .

Линейность означает, что определены операции сложения элементов и их умножения на числовые множители так, что

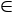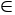• для любой пары элементов Z₁, Z₂ Q и любой пары чисел а₁, а₂ результат есть элемент того же пространства, т.е. а₁ Z₁ + а₂ Z₂ = Z₃ , Z₃Q;

• выполняются сочетательный, переместительный и распределительный законы умножения объектов на числа и сложения.

Эти условия в инженерно-технических задачах обычно соблюдаются.

В линейном пространстве задаётся нулевой элемент , такой, что

Z +  = Z и 0  Z =  для любого элемента ZQ .

Метричность означает, что между любыми элементами Z₁, Z₂ Q может быть определено расстояние (Z₁,Z₂), которое выражается числом и удовлетворяет следующим требованиям:

• ( Z₁, Z₂) 0; равенство возможно только при совпадении Z₁ и Z₂ ;

• ( Z₁, Z₂) = ( Z₂, Z₁) (аксиома симметрии);

• ( Z₁, Z₂) ( Z₁, Z₃) + ( Z₂, Z₃) , Z₃Q (аксиома треугольника).

Способ определения (Z₁,Z₂) называют метрикой пространства.

В пространствах из однотипных объектов метрику можно вводить по-разному. При этом и пространства считаются разными.

По аналогии с привычными геометрическими понятиями, элементы пространств часто называют точками этих пространств.

Множество точек, удаленных от точки Z₀ не более, чем на расстояние (Z, Z₀)  , называют -окрестностью Z₀ или -шаром с центром Z₀ .

Нормированность означает, что каждому элементу ZQ ставится в соответствие действительное число – норма (обозначается), такое, что:

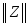• = 0 в том и только в том случае, когда Z = ;

• + ;

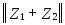
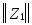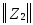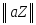• = a .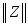

Норма обобщает понятие величины для элементов разных типов.

В линейном метрическом пространстве норму обычно определяют как расстояние между Z и нулевым элементом пространства: = (Z, ) .

Наоборот, нормированное пространство можно считать метрическим _{с метрикой, равной норме разности:} _{( Z1, Z2) =}.

Тип объектов пространства определяет, какие операции и преобразования могут к ним применяться.