2.6. 5. Концепции пространств и точность вычислений

Для обработки сложных объектов необходимо располагать оценками, которые рассматривались как оценка погрешностей скаляров.

Пусть Z – вычисляемый объект, Z^* – его искомое точное значение, – вычисленное приближенное значение. Тогда аналог предельной абсолютной погрешности оценивается в виде

Z  ( Z^*, ) или Z  . (2.6)

Аналогом относительной погрешности является Z=Z/ (2.7).

3. Обработка результатов измерении Постановка задачи

Методы и технологии аппроксимации( приближения) зависят от следующих факторов:

• тип исходного объекта – непрерывная функция, дискретный набор данных или объект более сложной структуры

• цель формирования аппроксимирующего выражения– последующие символьные выкладки, численные расчёты, качественный анализ и др.;

• выбранная для аппроксимации система базисных функций – целые степени аргумента x_i, косинусы и синусы кратных углов sin(ix) и cos(ix), экспоненты е(±ix) (во всех перечисленных случаях при i=0..n);

• линейность или нелинейность вхождения базисных функций в получаемое выражение;

• выбранный критерий оценки близости результата к исходному объекту;

• требуемый уровень близости согласно выбранному критерию.

В соответствии с этими факторами выбирается метод вычисления тех коэффициентов при базисных функциях, которые образуют искомый агрегат.

При необходимости проверяют, обеспечен ли нужный уровень близости.

Аппроксимация дискретных данных

Метод наименьших квадратов

Далее будем рассматривать аппроксимацию объектов, представленных в виде дискретных наборов данных или двух векторов ( объекты являются дискретными функциональными зависимостями).

А) Метод наименьших квадратов применяют, когда необходимо вывести формулу аппроксимирующей кривой, описывающей некоторую зависимость, полученную в результате, например, эксперимента. Поскольку экспериментальные данные получают, как правило, с некоторой погрешностью.

Поэтому , учитывая этот фактор уже на первых этапах аппроксимирующую кривую проводят таким образом , что она не проходит через экспериментальные точки, но в то же время учитывает исследуемую закономерность, сглаживая случайные выбросы результатов эксперимента.

В качестве аппроксимирующей функции может использоваться линейная комбинация F(x) любых функций

F(x)= a₀f₀(x)+a₁f₁(x)+ … + a_nf_n(x) , (1)

где f₀(x), f₁(x),…, f_n(x) - набор любых функций, называемых базисными; a₀ ,a₁ ,… ,a_n - набор коэффициентов.

Д овольно часто в качестве базисных функций используют комбинацию из возрастающей степенной последовательности аргумента f₀(x)=1, f₁(x)=x, f₂(x)=x²,…, f_n(x)=xⁿ , при этом аппроксимирующая функция будет являться алгебраическим полиномом.

Пусть некоторая функция задана таблицей значений y_i в узлах x_i (i=0,1,2,…,m) , где (m+1) – количество узлов (см. рисунок).

Исходные данные представлены в табл.

i	0	1	-	k
xi	x0	x1		xk
yi	y0	y1	­	yk

Требуется определить коэффициенты a₀ ,a₁ ,… ,a_n полинома

P (x)=a₀+a₁x+ … +a_nxⁿ (2)

таким образом, чтобы сумма S квадратов отклонений полинома P (x) от значений y_i аппроксимируемой функции в заданных точках была бы минимальной, т.е.

(3)

Если степень полинома n = m , то полином (2) будет интерполяционным и пройдет через все узлы и отклонения будут нулевыми.

Стремясь понизить степень полинома, принимают n < m, при этом в общем случае аппроксимирующая кривая не будет проходить через заданные точки (x_i, y_i) . Сумма квадратов отклонений зависит от коэффициентов полинома a₀ ,a₁ ,… ,a_n .

Поскольку функция S принимает только положительные значения и имеет минимум, вычислим частные производные по всем переменным a₀ ,a₁ ,… ,a_n и приравняем их нулю:

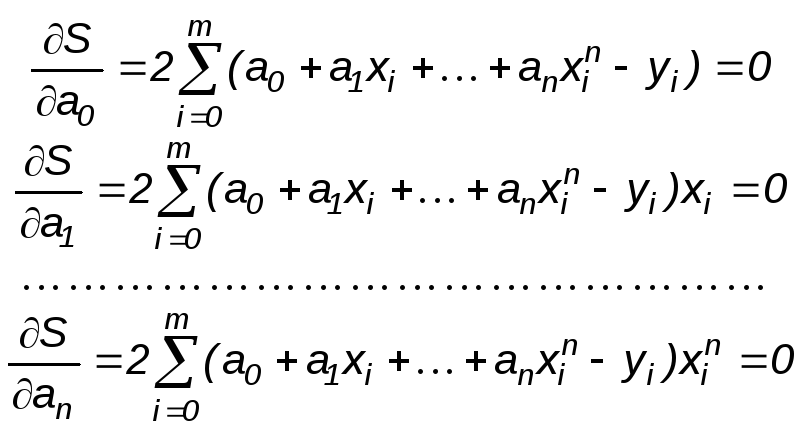
Выполнив суммирование, собрав коэффициенты при каждом a₀ ,a₁ ,… ,a_n и перенеся не содержащие их суммы в правую часть, получим СЛАУ относительно неизвестных a₀ ,a₁ ,… ,a_n :

В матричной форме эту систему можно записать как aS = b , где

Решение этой системы позволяет найти все коэффициенты a₀ ,a₁ ,… ,a_n и значение полинома в любой точке x вычисляют по формуле (2)

Для полиномиальной аппроксимации (регрессии) в MathCAD’е можно воспользоваться следующими встроенными функциями:

1. regress(x,y,k) – возвращает вектор коэффициентов a полинома, при этом всегда первые три компоненты вектора есть вектор вторых производных и являются параметрами для описываемой ниже функции interp , а остальные компоненты и есть вектор коэффициентов a , где

x - вектор данных аргумента, элементы которого должны быть расположены в порядке возрастания;y - вектор значений того же размера;

k - степень полинома (целое положительное число).

Функция regress позволяет, вычислить коэффициенты a₀ ,a₁ ,… ,a_n , построить полином в форме (2) и уже его использовать, например, для построения графика.

Н апример, при значении степени полинома k=2 функция regress возвратит представленное справа значение.

2. interp (s,x,y,t) – возвращает результат полиномиальной регрессии, где

s - вектор вторых производных, созданный, например, предыдущей функцией;

x и y - то же, что и в предыдущей функции;

t - текущее значение аргумента полинома.

Функция interp позволяет непосредственно вычислить значение полинома при любом значении аргумента без построения полинома как такового

3. linfit(x,y,F) – более универсальная функция, возвращающая вектор коэффициентов a линейной комбинации функций (1), где

x и y - то же, что и в предыдущей функции;

F - вектор базисных функций f₀(x), f₁(x),…, f_n(x) в выражении

Н апример, для алгебраического полинома степени n =2 необходимо записать F в следующем виде:

Функция linfit также позволяет непосредственно вычислить значение полинома при любом значении аргумента без построения полинома как такового.

Рассмотрим пример: