Vychmat_lektsii / Лекция 14 Monte-Carlo

Лекция 14

Метод Монте-Карло.

Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений. Сам метод слагается из трех составных частей. Это, во-первых, моделирование случайных величин с заданным законом распределения, во-вторых, построение вероятностных моделей реальных процессов (систем) и, наконец, задачи статистической теории оценивания. Его применение оправдано в первую очередь, в тех задачах, которые допускают теоретико-вероятностное описание. Метод оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики. К разделам науки, где в большей мере используется метод Монте-Карло, следует отнести задачи массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других. Среди других вычислительных методов метод Монте-Карло выделяется своей простотой и общностью. Медленная сходимость является существенным недостатком метода.

Принципиальная основа использования метода Монте-Карло- это теорема Колмогорова или усиленный закон больших чисел.

Теорема:

Чтобы среднее арифметическое независимых (испытаний) реализаций случайной величины сходилось с вероятностью единица к её математическому ожиданию необходимо и достаточно, чтобы математическое ожидание существовало.

Использование центральной предельной теоремы дает возможность оценивать погрешность метода. Для этой цели нужно уметь оценивать дисперсию. Очевидно, что параллельно с оцениваем математического ожидания случайной величины можно оценивать и математическое ожидание квадрата случайной величины и, следовательно, её дисперсию. Считая N достаточно большим и оценку для дисперсии достаточно точной, можно с заданной вероятностью получить неравенство:

,

если p- заданное значение вероятности, то γ находится из соотношения

Исходной случайной величиной при использовании метода Монте-Карло является одномерная равномерно распределенная на промежутке [0,1] случайная величина α, т.е. случайная величина с плотностью распределения

.

В практических расчетах наиболее удобно получать реализации α при помощи алгоритма, построенного на основе реккуррентных соотношений. Числа, полученные таким путем называются псевдослучайными.

Имея в нашем распоряжении реализацию случайной величины α, мы можем получить реализацию случайной величины с заданным законом распределения. Пусть ξ распределена по закону F_ξ(x), тогда .

Например:

1), тогда .

2) Если ξ распределена по нормальному закону, имеющему среднее значение равное 0 и дисперсию равную 1, то практически .

3) Пусть требуется получить случайные числа Х_i с законом распределения:

f(x) = λ(1- λ/2 x), x € [0,2/λ],

который находит применение при решении задач теории массового обслуживания, тогда

x_i = 2/λ(1 - ).

4) Если задана плотность вероятности f(x) = c/(1+bx)², х € [0, 1/(с – b)], то

X_i = α_i/(c – bα_i).

5) Аналогично, если случайные величины распределены по релеевскому закону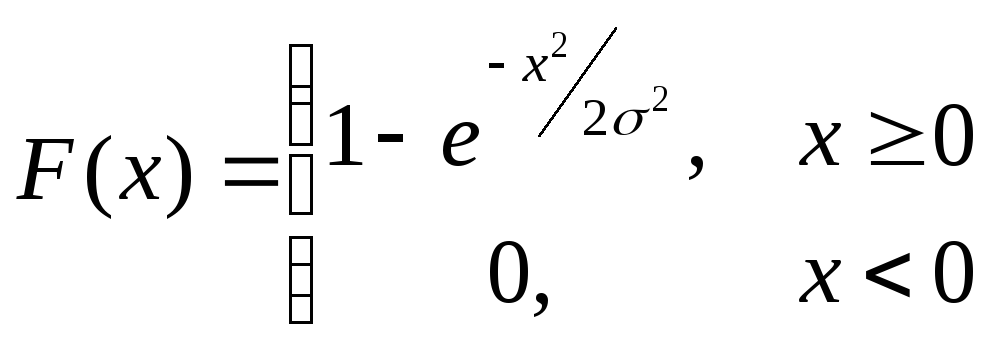, то

, то

S_i = σ.

Это распределение играет существенную роль в радиотехнических задачах.

6) В некоторых задачах приходится оперировать со случайными величинами η, распределенными по закону Парето:

,

тогда η = α^-1/β,

особенно легко пользоваться им, если β = 1/k, где k – целое число.

Аналогично можно реализовать дискретные и многомерные случайные величины.

Располагая сведениями, изложенными выше, можно решать практические задачи путем имитации вероятностной модели некоторого реального явления. Особенность метода Монте-Карло состоит в том, что его применение не требует, вообще говоря, формулировки интегро-дифференциального уравнения, описывающего потоки частиц или системы дифференциальных уравнений, описывающей систему массового обслуживания. Н а практике формулировка подобных уравнений и их реализация представляют значительные трудности.

Изложим, по существу, схему моделирования, которая отражает, однако, физическую суть явлений переноса частиц. Пусть имеется некий объем D, заполненный частицами вещества и окруженный вакуумом. Частица характеризуется своим положением в пространстве , временной координатой t, направлением движения – единичным вектором и скоростью V (или энергией E). Таким образом, величины, характеризующие частицу, это точка с семимерном фазовом пространстве (ибо ).

Будем предполагать:

а) Концентрация частиц в объеме мала, так что можно пренебречь их взаимодействием друг с другом, но можно учесть и редкие столкновения.

б) Частицы взаимодействуют с веществом таким образом, что вероятности различных видов взаимодействия не зависят от предыстории частицы.

в) Вещество находится в стационарном состоянии, то есть плотность вещества и ее состав не меняются в зависимости от времени.

При сформулированных предположениях процесс слагается из независимых «историй». Прослеживая эти истории, можно получить различные характеристики процесса. История частиц начинается ее рождением. В области Т фазового пространства координаты частицы задаются функцией распределения источников . Моделируя это распределение в момент времени t₀, получим начальные координаты частицы(). Далее частица движется прямолинейно и равномерно(или по параболе, если учитывается влияние гравитации или электромагнитного поля) до столкновения со стенками изучаемого объема или до столкновения с другой частицей. Вероятность столкновения в пути определяется экспериментально или по данным теоретического расчета, если это возможно. История частицы отслеживается до ее выхода из объема или до ее поглощения. Результатами расчета обычно являются некоторые средние значения – например, среднее число частиц, покинувших объем, поглотившихся в некотором объеме и т.п. Более сложными по своей реализации являются задачи, в которых требуется определить распределение частиц в зависимости, от каких либо характеристик (энергии, направления и т.п.).

Метод Монте-Карло позволяет моделировать задачи массового обслуживания, характеризуемые потоком заявок, который задается функцией совместного распределения интервалов времени между поступлениями двух последовательных заявок; наличием некоторого количества обслуживающих приборов. Время обслуживания прибора определяется случайной величиной со своей функцией распределения; заявки, поступающие в момент, когда приборы заняты, образуют очередь; так же заявки характеризуются дисциплиной ожидания и обслуживания, последние определяются некоторыми распределениями вероятностей.

Можем изучать поведение различных популяций, разыгрывая поведение особей внутри сообщества и внешнее влияние на него на базе теории Марковских процессов. При этом оценивается устойчивость популяции или сроки её вымирания.

Можно рассматривать имитации танковых сражений и многое другое.

Рассмотрим применение метода Монте-Карло в вычислительной математике. Метод Монте-Карло является универсальным методом и позволяет стохастически решать те же задачи, что и детерминированные методы вычислительной математики. Разберем некоторые из них:

а) приближенное интегрирование методом Монте-Карло

оценивается с помощью среднего арифметического

,

где x_i –независимы и их распределение задается мерой μ.

Характер его сходимости вероятностный.

,

где I(f) –точное значение интеграла

,

дисперсия , , если , то выполняется с вероятностью 0,997, т. е. по правилу «трех сигм» и при условии, что для функции f(x) существует и конечный интеграл .

Вычисление двойных интегралов методом Монте-Карло.

,

,

Цилиндрическое тело, содержащее данный объем V=(b-a)(d-c)T.

,

где

N - количество реализаций;

m - количество реализаций, попавших во внутреннюю часть искомого объема;

- независимые реализации случайной величины равномерно распределенной соответственно для , ,.

Порядок оценки сходимости в этом случае тот же, т.е. .

Этот порядок не зависит от размерности интеграла в методе Монте-Карло, в то время как порядок гарантированных оценок сходимости в детерминированных методах существенно ухудшается с ростом размерности.

б) Метод Монте-Карло решения систем линейных алгебраических уравнений.

Рассмотрим систему линейных алгебраических уравнений, записанную в векторной форме:

АХ = b

А – nxn матрица, Х и b – n-мерные векторы. Пусть имеет место случай, когда пригоден метод простой итерации, т.е. матрица А представима в виде:

А = Е – В

где Е – единичная матрица, а В – матрица, имеющая собственные числа, по модулю меньшие единицы.

Модель строится по принципу Марковского процесса, заканчивающегося с вероятность единица за конечное число шагов. Исходная система эквивалентна:

Х = ВХ + b. (1)

Решение исходной системы представимо в виде:

Х = A^-1b. (2)

При сделанных предположениях, сравнивая (1) и (2), обратная матрица может быть выражена рядом:

А^-1 = Е + В + В² + …+ Вⁿ + … (3).

Этот ряд сходится тогда и только тогда, когда l(B)l1. Подставим теперь выражение (3) в (2) и получим:

Х = b + Bb + B²b +…+ Bⁿb + …

Частные суммы этого ряда можно получить известным итерационным приемом, полагая последовательно Х⁽¹⁾ = b, Х⁽²⁾ = ВХ⁽¹⁾ = Bb + b,…, Х^(к) = ВХ^(к-1) = B^k-1b+ B^k-2b + …+ Bb + b, при этом последовательность Х⁽ⁿ⁾ сходится к Х при n  .

Для вычисления Х перейдем к координатной записи. Обозначим элементы матрицы В через В_ij, тогда m – я координата вектора Х равна:

Х_m = b_m + B_mi b_i + B_mi1 B_i1i2 b_i2 + … + B_mi1 B_i1i2 … B_ir-1ir b_r + … (4)

Вопрос состоит в том, чтобы найти метод вычисления этой суммы. Рассмотрим сначала случай, когда элементы матрицы не отрицательны и сумма элементов по каждой строке равна единице:

B_mi = 1,

тогда величины B_mi можно рассматривать как набор вероятностей для полной системы несовместных событий. Эти события можно рассматривать как выборку шаров из n урн.

Пусть в каждой из n урн лежать шары n различных сортов. Пусть В_mi – вероятность вытащить из m-й урны шар i-го сорта. Вынем наугад шар из m-той урны и образуем случайную величину _m, выбрав в качестве ее значения bi, если вынут шар i-го сорта.

Математическое ожидание _m равно Е_m = B_mi b_i, т.е. второе слагаемое ряда (4).

Теперь получим случайную величину, математическое ожидание которой равно третьему слагаемому ряда (4). Для этого обратимся сначала к m-й урне и вынем из нее шар. Если он оказался i1-го сорта, то обратимся к i1-й урне. Если из нее вынут шар i2-го сорта, то положим значение величины _m равным b_i2. Ясно, что вероятность, с которой случайная величина _m принимает значение b_i2, равна:

B_mi1 B_i1i2,

тогда математическое ожидание величины _m равно:

Е_m = B_mi1 B_i1i2 b_i2.

Обобщая эти рассуждения и далее, мы получим ряд (4), т.е.

Хm = E_m,

тогда, моделируя процесс получения величины _m N раз, мы можем принять в качестве приближенного значения искомой величины Хm – среднее арифметическое:

_m = (_m¹ + _m² + … + _m^N)/N.

Теперь перейдем к нашему случаю. Для этого представим каждый элемент B_mj матрицы B в виде произведения двух сомножителей:

B_mj = F_mj P_mj,

где P_mj  (0,1).

Координаты вектора правой части системы запишем в виде:

b_m = F_m P_m,

где P_m  (0,1).

При этом будем предполагать, что выполнено условие:

P_m + P_mi = 1,

тогда равенство (4) можно представить в виде:

Хm = F_m P_m + F_mi F_i P_mi P_i + … + F_mi1 F_i1i2 F_i2i3 … F_ir-1ir F_ir P_mi1 … P_ir-1ir P_ir (5).

Пусть у нас имеется n урн, в каждой из которых лежат шары n+1-го сорта. Вероятности вытащить из к-ой урны шар одного из сортов равны:

P_k1, P_k2, … , P_kn, P_k.

Начнем с m-ой урны, и вынем из нее шар. Если вынут шар сорта i1 (i1  n), то затем нужно обращаться в i1-ю урну. Если же вынутый шар n+1-го сорта, то дальнейшее обращение к урнам на этом прекращается и в этом случае в качестве значения для случайной величины _m берется число F_m. Если шар n+1-го сорта оказался вынутым из

ir-ой урны после того, как последовательно вынимались шары из урн с номерами: m, i1, i2, … , ir-1, то значение величины _m полагается равным:

F_mi1 F_i1i2 … F_ir-1ir F_r.

Вероятность того, что случайная величина _m примет данное значение, равна:

W_mi1i2…ir = P_mi1 P_mi2 … P_ir. (6)

Математическое ожидание величины _m:

E_m = W_mi1i2…ir F_mi1 F_i1i2 …F_ir. (7)

Подставим (6) в (7) и сравнивая с (5), получим:

Xm = E_m.

Таким образом, моделирование случайной величины _m позволяет получить Хm с определенной вероятностью. Преимущество изложенного метода решения состоит в том, что при обычном методе решения систем линейных уравнений для вычисления одного неизвестного нужно определять и все остальные, в приведенном способе этого делать не нужно, ибо каждый раз определяется одна координата. Это означает, что число арифметических операций пропорционально числу уравнений, а не кубу этого числа, как в численных методах. Отсюда видно, что и здесь проявляется одна из основных черт метода Монте-Карло – его эффективность при решении многомерных задач.

в) Решение задачи Дирихле методом Монте – Карло.

∆U(x,y) = 0 (x,y) € G, U(x,y) │_{(x,y) € Г} = φ(x,y),

Г – контур, ограничивающий область G, кусочно-гладкая кривая.

В области G строим квадратную сетку S_h с шагом h,

x_i = x₀ + ih, y_i = y₀ + jh (i, j = 0 ± 1, ± 2, ± 3, …),

где ∆x_i = x_i+1 – x_i = h ∆y_i = y_i+1 – y_i = h (h>0).

Граничные узлы сетки S_h образуют ее границу Г_h , т.е. граничные узлы – ряд точек M_pq (х_p , y_q), аппроксимирующий криволинейную границу Г области G с точностью до h.

Пусть точка M блуждает равномерно по узлам сетки (1), т.е., находясь во внутреннем узле M_ij (x_i , y_j). Эта частица за один переход с вероятностью р = ¼ может переместиться в один из четырех соседних узлов, причем каждый такой переход не зависит от положения частицы на сетке и от ее прошлой историю. Блуждание частиц заканчивается как только она попадет на границу Г_h – это поглощающий экран. Доказано, что с вероятностью р = 1 блуждание точки М через конечное число шагов закончится на границе. Если частица М начала свое блуждание с фиксированной точки изнутри М_i0j0 сетки S_h , то конечная совокупность последовательных положений этой частицы:

М_i0j0 , М_i1j1 , … , М_isjs , где М_isjs принадлежит Г, но при k = 0, 1, 2, … , S – 1

М _ikjk не принадлежит границе Г, тогда эта последовательность называется траекторией частицы или историей ее блуждания. Пусть в точках границы Г определена функция φ(x,y). Перенесем это значение на границу Г_h сетки S_h . Для каждого граничного узла M_pq (х_p , y_q), принадлежащего границе Г_h определим ближайшую по горизонтали или вертикали точку N, принадлежащую границе Г и положим

φ(M_pq) = φ(N) = φ(х_p , y_q) = φ_pq . Пусть вероятность Р(i, j, p, q) – есть вероятность того, что траектория частицы, вышедшей из узла М_ij сетки S_h , закончится в граничном узле M_pq , принадлежащим Г_h .

Составим сумму V_ij = φ_pq.

Эту сумму можно рассматривать как математическое ожидание функции φ(x, y) на границе Г_h для траекторий, начинающихся в точке М_ij . Причем оказывается, что искомые неизвестные U_ij задачи Дирихле можно рассматривать как математические ожидания V_ij .

Рассмотрим достаточно большое число N равномерных случайных блужданий частицы по узлам сетки S_h , исходящих из фиксированного узла М_ij и заканчивающихся на границе Г. Пусть (, ), при k = 1, 2, … , N соответствующие точки выхода частицы на границу Г_h . Заменяя математическое ожидание V_ij эмпирическим математическим ожиданием, будем иметь

U_ij ≈ V_ij = 1/N.

Эта формула дает статистическую оценку величины U_ij и может быть применена для приближенного решения задачи Дирихле.

Недостатком рассмотренного метода для задачи Дирихле является слабая сходимость по вероятности при эмпирического математического ожидания:

= 1/N,

к математическому ожиданию V_ij = U_ij .

Естественно, что блуждание частицы М, начинающееся в точке М_ij , автоматически является случайным блужданием частицы, начинающейся в любой промежуточной точке траектории этой частицы.