Оценка общей погрешности численного дифференцирования.
При определении
общей погрешности численного интегрирования
надо понимать , что помимо остаточного
члена есть погрешность задания весов
( коэффициентов ) в формулах и погрешность
вычисления значений функции в узлах.
Таким образом , абсолютная погрешность
численного определения интеграла может
быть представлена в виде:

∆qi
- абсолютная погрешность весов,
∆ξi
- абсолютная погрешность узлов
При компьютерном
вычислении можно считать
∆qi
≈∆ξi
≈ε , 0 ≤ i
≤ n-1
, ε- точность представления вещественных
чисел
Видно , что для
оценки погрешности надо иметь числовую
оценку модуля функции и ее первой
производной.
Пусть это будут
величины М0
и М1.
∆I=nε(М0+М1)+│R│
Если далее аналогично
предположить , что существуют такие М2
и М4
для второй и четвертой производных ,
то получим выражения для ∆I
формул прямоугольников, трапеций и
Симпсона .



Существует
абсолютная погрешность ∆Imin
для любой квадратурной формулы, которую
нельзя уменьшить увеличивая число
шагов.
Конкретное значение
зависит от М0,
М1,
М2,
М4,
а, в, ε .
Правило
Рунге оценки погрешности квадратурной
формулы
Для оценки
погрешности любой квадратурной формулы
с шагом h/2
следует вычислить численный интеграл
по той же формуле с шагом h
, тогда погрешность первоначального
вычисления имеет величину

На практике для
прямоугольников и трапеций , формулы
Симпсона
 ,
,

В основе этого
правила уточнения лежит экстраполяция
Ричардсона.
Идея экстраполяции
Ричардсона в том , чтобы из значений
Qh/2
и Qh
составить такую линейную комбинацию
Qh/2,h=c1
Qh/2
+ c2
Qh
,
чтобы погрешность
приближения интеграла I
с помощью этой линейной комбинации
Qh/2,h
была более высокого порядка h
, чем Qh/2
и Qh
по отдельности
Коэффициенты
выбираются
в виде
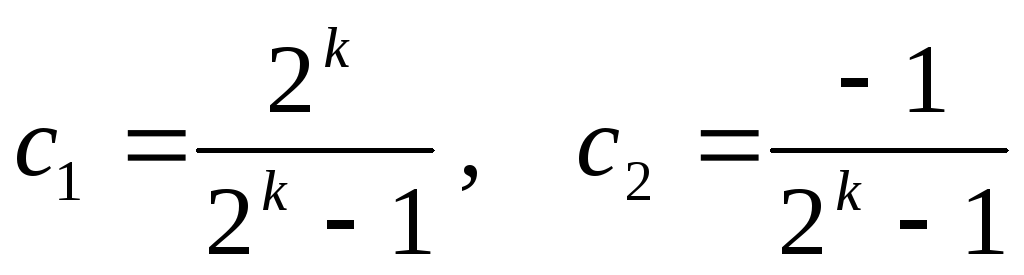
13



 ,
,
