- •Статистика
- •Содержание
- •Ряды распределения.
- •1. Атрибутивные ряды распределения
- •2. Вариационные ряды распределения
- •Графическое изображение.
- •Эмпирическая функция распределения.
- •Средние величины.
- •2. Структурные средние.
- •Показатели вариации
- •Ряды динамики.
- •Изучение тренда.
- •Статистическая и корреляционная зависимость.
- •Корреляционная таблица.
- •1. Представим результаты эксперимента в виде корреляционной таблицы:
- •Уравнение регрессии и коэффициент корреляции величин, заданных числовыми массивами.
- •Эмпирическая функция распределения
- •Степенные средние величины
- •Показатели вариации
- •Средняя величина и анализ динамики
- •Изучение тренда
- •Линейная корреляция
- •Библиографический список:
Графическое изображение.
Для наглядного представления статистического распределения пользуются графическим изображением вариационных рядов: полигоном и гистограммой.
Таблица
-
x1
x2
…
xm
n1
n2
…
nm
в
первой строке которой расположены
варианты, а во второй – соответствующие
им частоты, называется дискретным рядом
распределения. Если на плоскости в
прямоугольной системе координат построим
точки(![]() ,
,![]() )и
соединим их последовательно отрезками
прямых, то получим ломаную линию, которая
называется полигоном
частот
(см.рис. 1)
)и
соединим их последовательно отрезками
прямых, то получим ломаную линию, которая
называется полигоном
частот
(см.рис. 1)
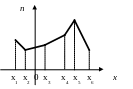
Рис.1
Полигон частот дает приближенное наглядное представление о характере распределения случайной величины.
Таблица
-
h1-h2
h2- h3
…
hm- hm+1
n1
n2
…
nm
в первой строке которой находятся частичные интервалы, а во второй соответствующие им частоты называется интервальным вариационным рядом.
Гистограммой
частот
называется ступенчатая фигура, состоящая
из прямоугольников, в основании которых
находятся частичные интервалы, а высотой
служит величина
![]() ,
которая называется плотность частоты
( рис.2).
,
которая называется плотность частоты
( рис.2).
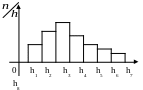
Рис.2
Пример. Дано распределение:
x |
171 |
175 |
179,8 |
184 |
188,2 |
192,8 |
n |
3 |
4 |
10 |
12 |
5 |
4 |
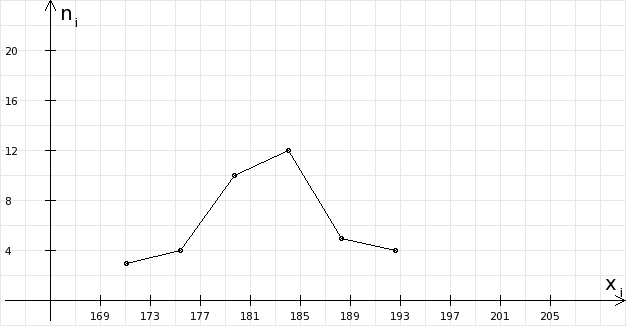
Задание: построить полигон частот.
Решение. Соединим точки (171;3),(175;4),(179,8;10),(184;12),(188,2;5),(192,8;4).
См.рисунок.
Пример По данному интервальному ряду построить гистограмму.
h |
10-260 |
260-510 |
510-760 |
760-1010 |
1010-1260 |
1260-1510 |
n |
4 |
6 |
15 |
18 |
8 |
6 |
Решение.
Ширина интервала h=250. Рассчитаем плотность частоты
h |
10-260 |
260-510 |
510-760 |
760-1010 |
1010-1260 |
1260-1510 |
n |
4 |
6 |
15 |
18 |
8 |
6 |
n/h |
0,016 |
0,024 |
0,06 |
0,072 |
0,032 |
0,024 |
Строим гистограмму, см..рисунок.

Эмпирическая функция распределения.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х
F*(x)=nх/n
где nх – число вариант, меньшее х, n – объем выборки
Таким образом, для того, чтобы найти, например F*(x2), надо число вариант, меньшее x2, разделить на объем выборки n: F*(x2)=nх2/n
Cвойства : 1. Значения эмпирической функции принадлежат отрезку [0;1] 2. F*(x)-неубывающая функция 3. Если х1 – наименьшая варианта, то F*(x)=0 при х≤х1; если хk – наибольшая варианта, то F*(x)=1 при х>хk.
Пример. Вычислить значения эмпирической функции по данному распределению выборки:
Варианты |
xi |
2 |
6 |
10 |
Частоты |
ni |
12 |
18 |
30 |
Решение:
Найдем объем выборки: 12+18+30=60.
Наименьшая варианта х=2, значит по свойству эмпирической функции для всех х≤2 функция равна нулю. Наибольшая варианта х=10 , значит для всех х>10 эмпирическая функция равна единице.
На
промежутке
![]() 2<
х≤ 6 F*(x)=12/60 = 0,2
2<
х≤ 6 F*(x)=12/60 = 0,2
6< х≤ 10 F*(x)=(12+18)/60 = 30/60=0,5
Ответ:

Пример Построить эмпирическую функцию по данному распределению выборки:
х |
5 |
5.5 |
6 |
6.5 |
7 |
7.5 |
n |
10 |
15 |
20 |
15 |
30 |
10 |
Решение.
Вычислим объем выборки: n= 10+15+20+15+30+10= 100
Рассчитаем значения эмпирической функции на промежутках:
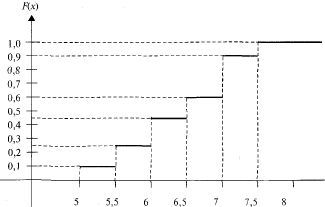
х ≤ 5 F*(x)=0 по свойству
5 < х ≤ 5.5 F*(x)=10/100=0,1
5.5 < х ≤ 6 F*(x)= (10+15)/100=0,25
6 < х ≤ 6.5 F*(x)= (10+15++20)/100=0,45
6.5 < х ≤ 7 F*(x)= (10+15+20+15)/100=0,6
7 < х ≤ 7.5 F*(x)= (10+15+20+15+30)/100=0,9
х > 7.5 F*(x)=1 по свойству
Построим на координатной плоскости. См.рисунок