
Пусть , , .
В лотерее 10 билетов; среди них 4 выигрышные. Участник лотерей покупает билетов. Пусть - {среди купленных билетов имеется выигрышных}.
В группе спортсменов человек. Среди них мастера спорта. На допинг по очереди проверили 5 человек. Пусть - {спортсмены прошли проверку в последовательности: мастер спорта, мастер спорта, не мастер спорта, не мастер спорта, мастер спорта}.
В подарочном наборе конфет, среди которых шоколадные. Одну конфетку (неизвестно какую) съели. А затем из оставшихся взяли конфету: она оказалась не шоколадной. Найти вероятность того, что съели шоколадную конфету.
Куплены телевизор, холодильник и утюг. Вероятности того, что они сломаются в течении гарантийного срока, равны соответственно , , . С.в. - число приборов, сломавшихся в течении гарантийного срока.
Вычислить
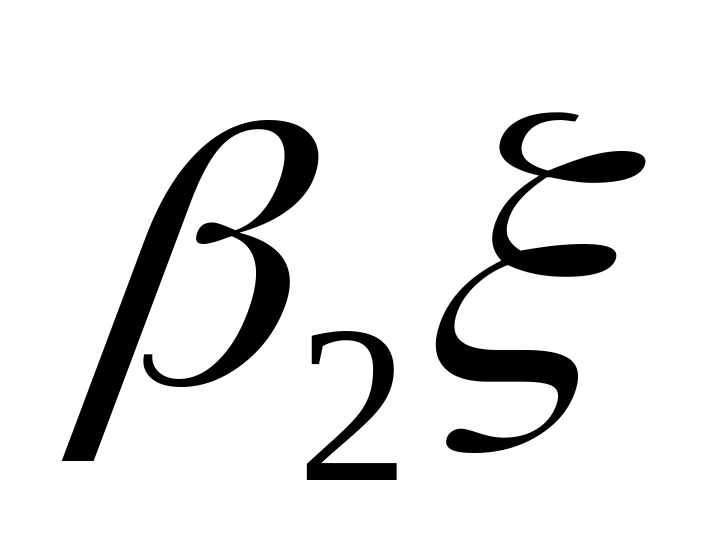 .
.-3
1
3
0,1
С.в. распределена равномерно в интервале . Известно, что
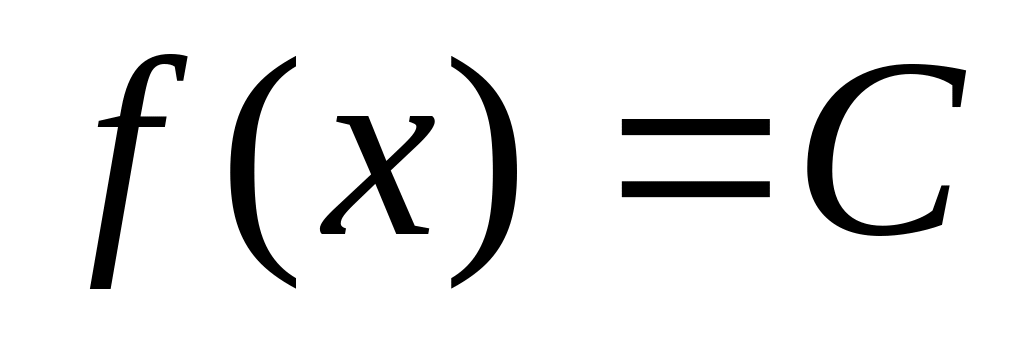 при
при
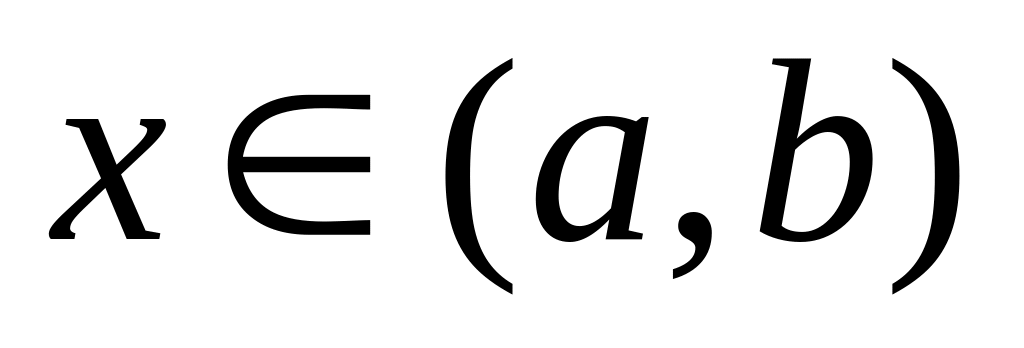 .
Найти
.
.
Найти
.
Пример данных к варианту №1
- {хотя бы одно сообщение передано неверно}.
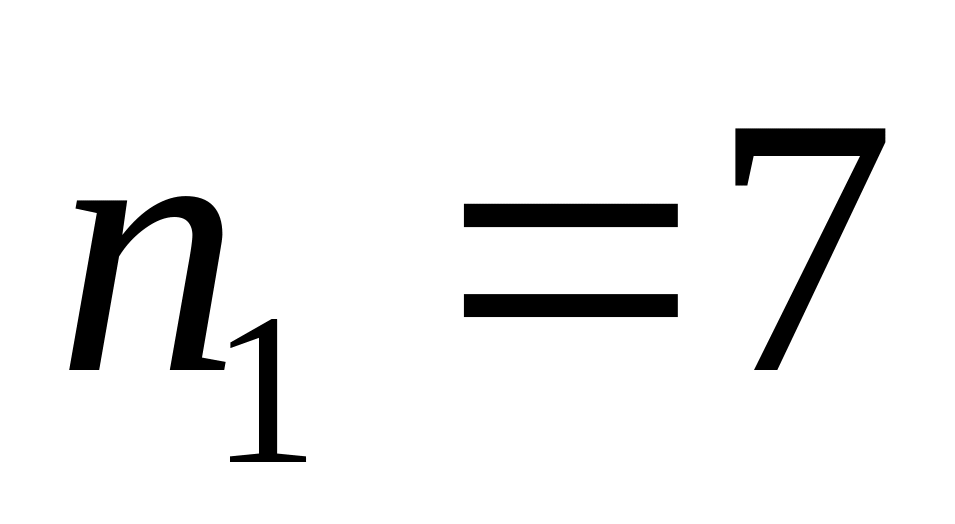 ,
,
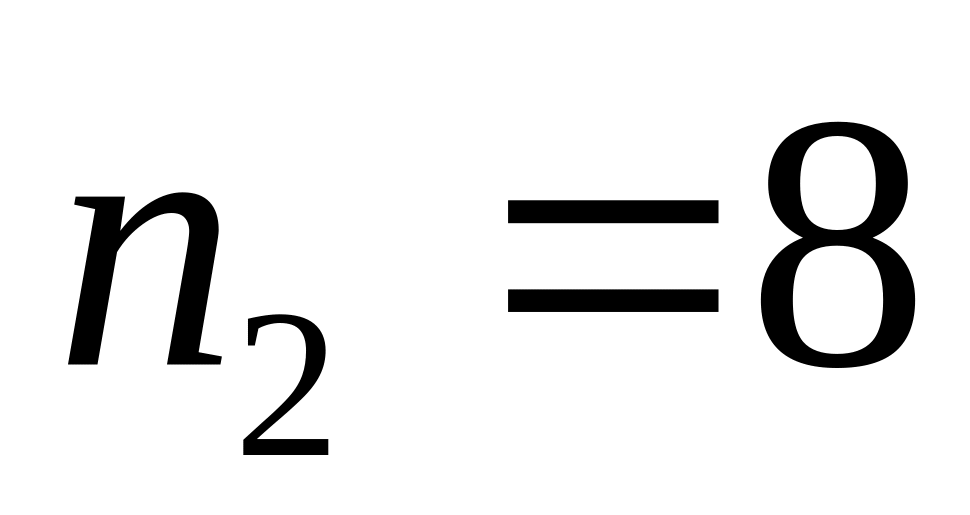 .
. ;
;
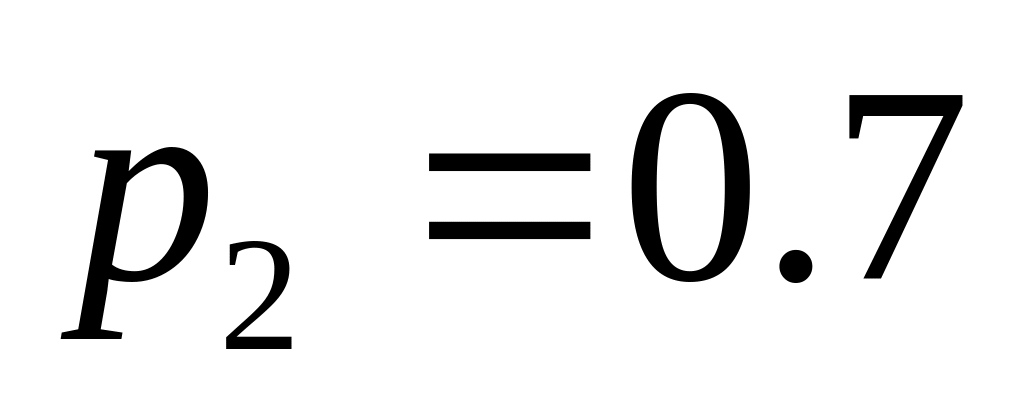 ;
;
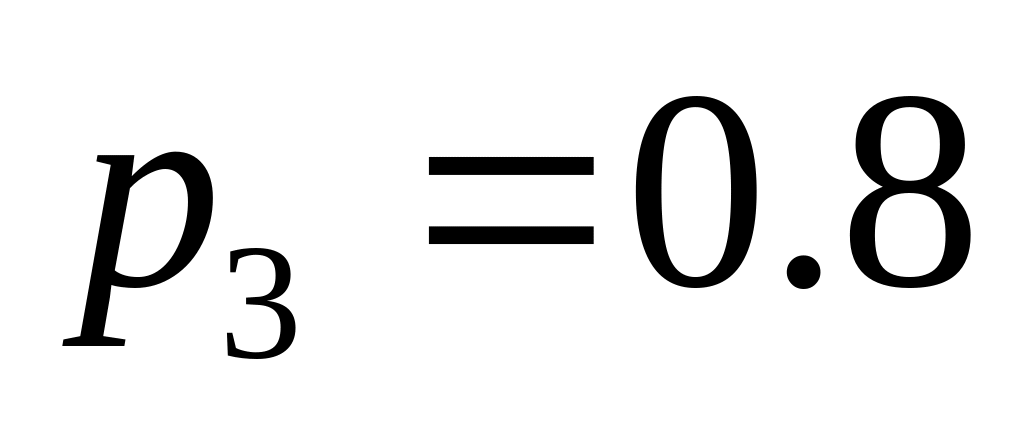 ;
;
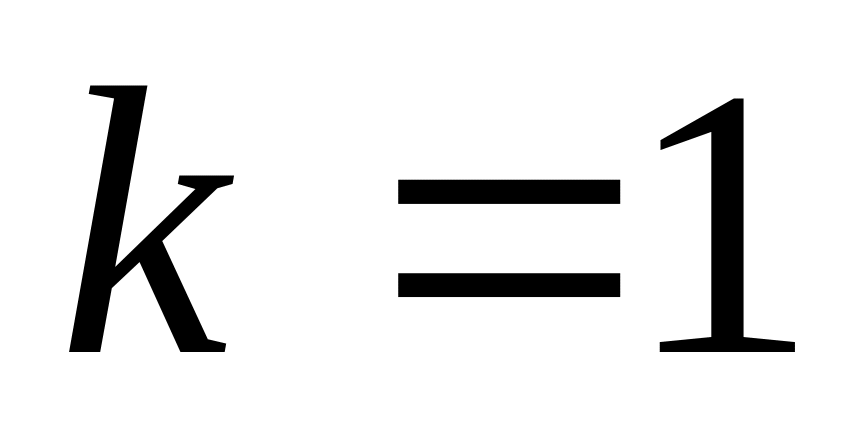 .
.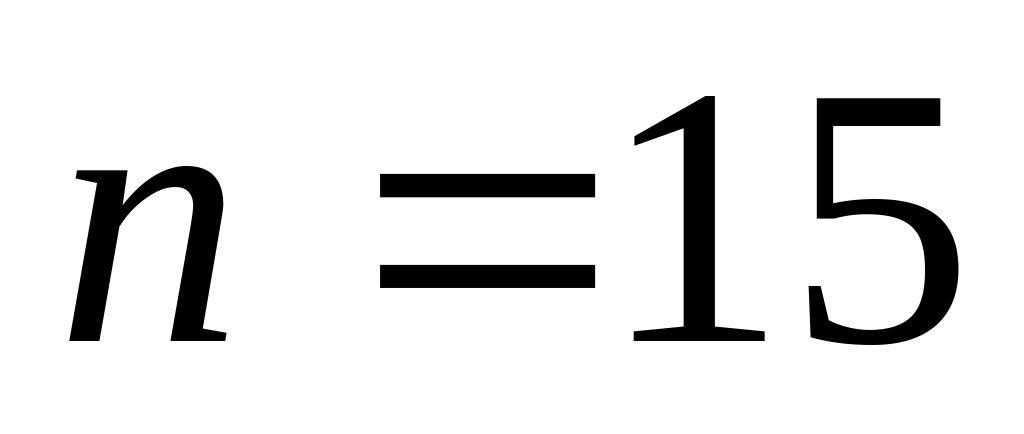 ;
;
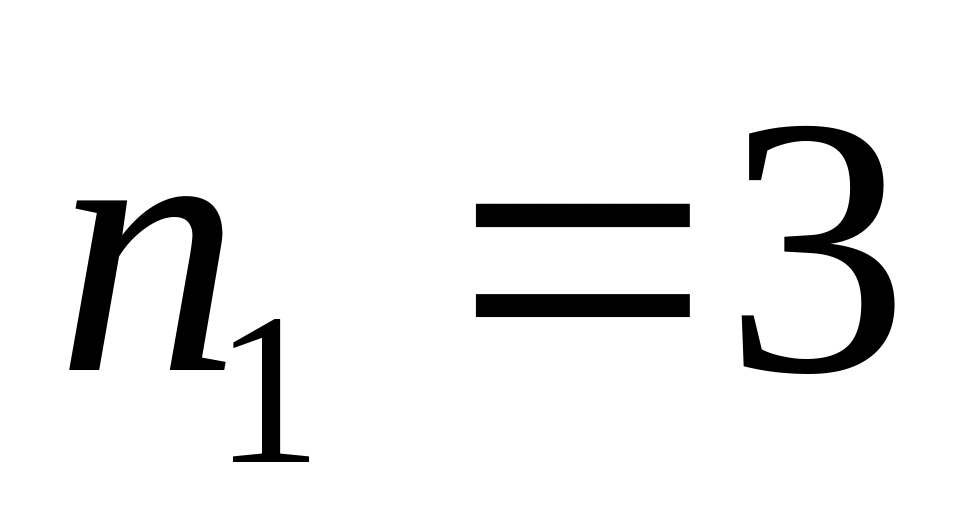 ;
;
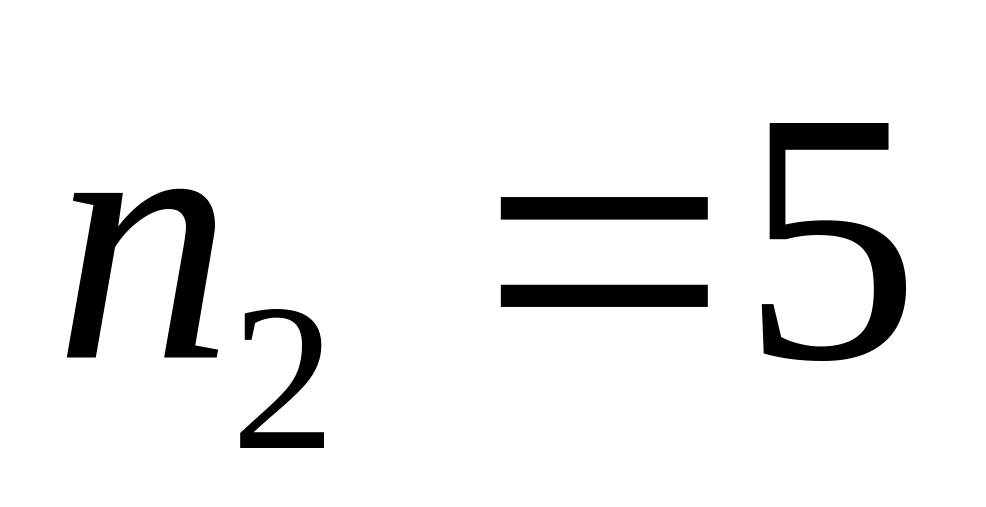 ;
;
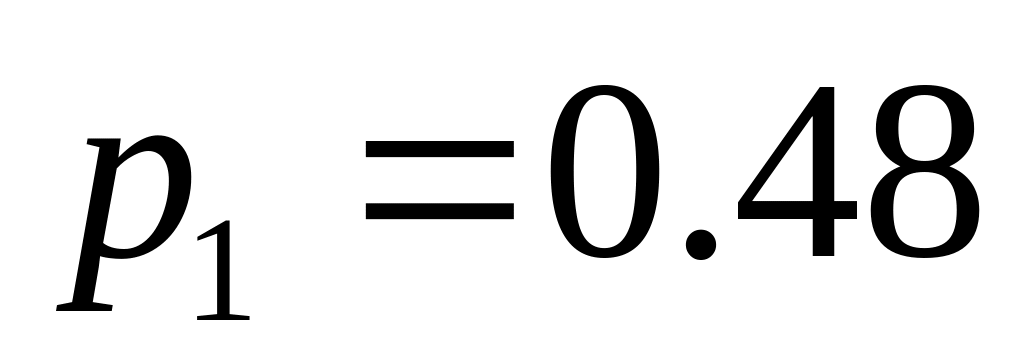 ;
;
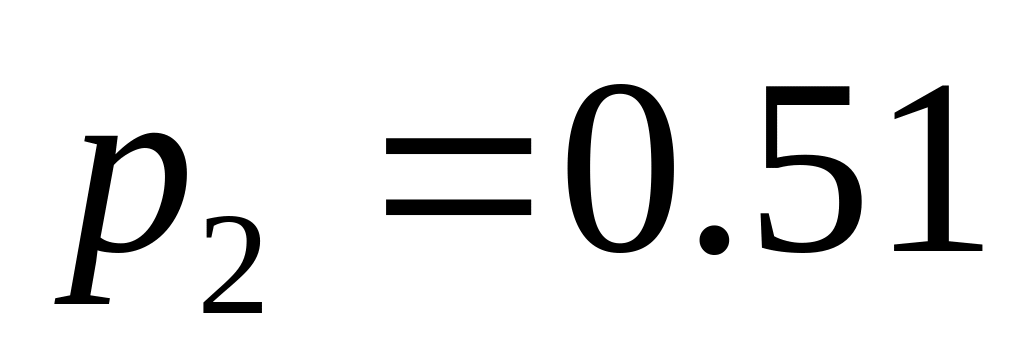 .
.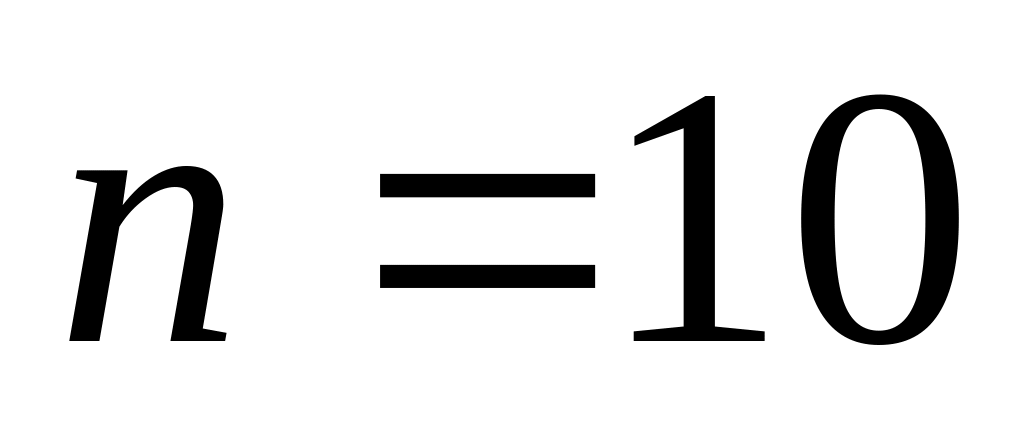 ,
,
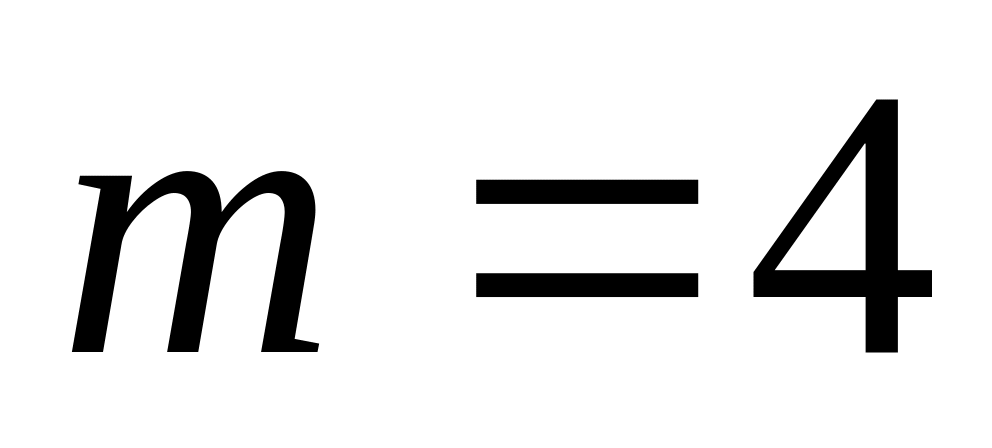 .
.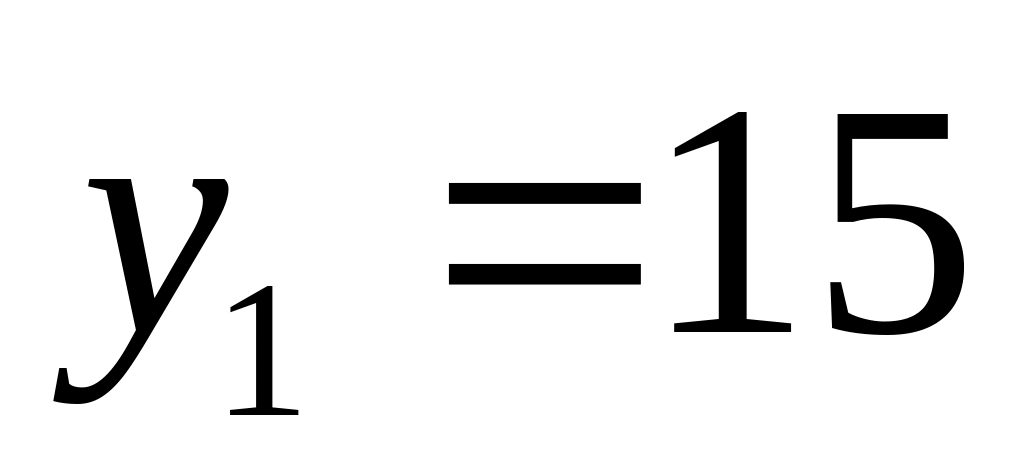 ,
,
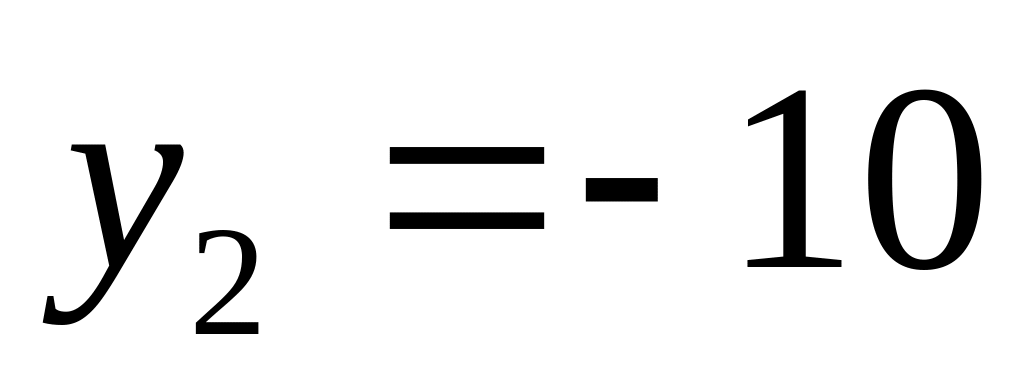 ,
,
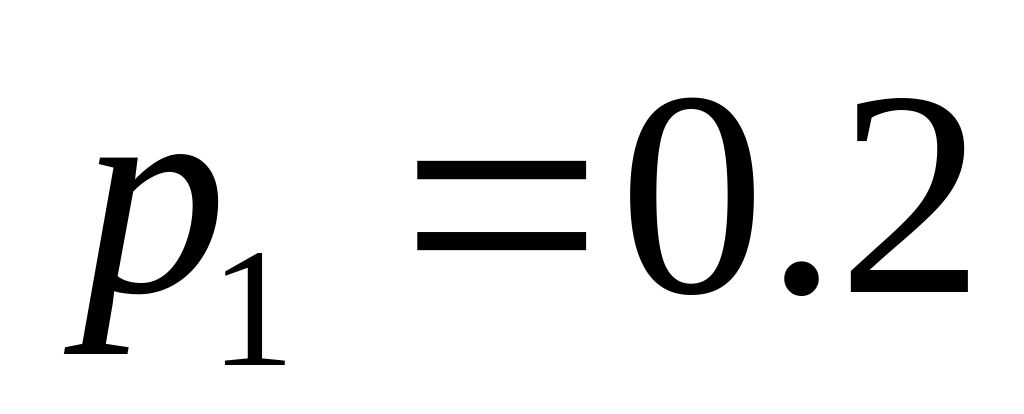 .
.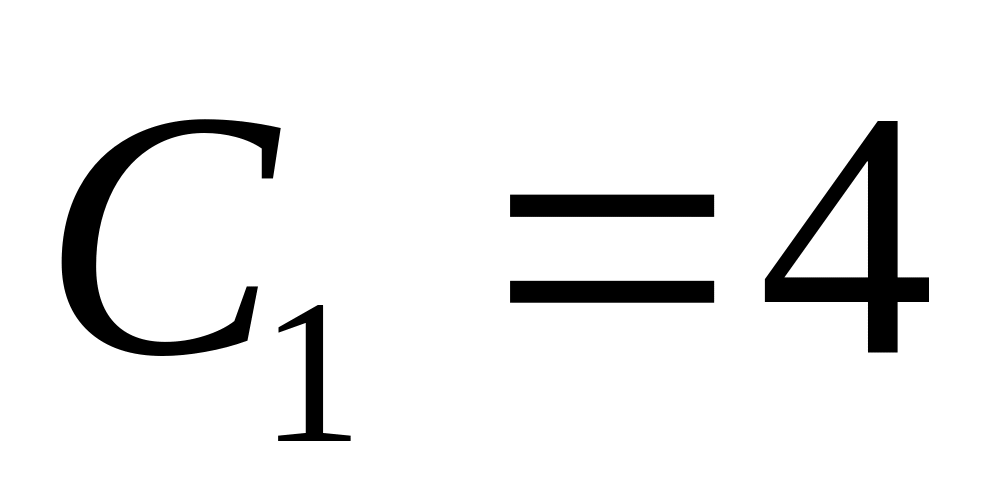 ,
,
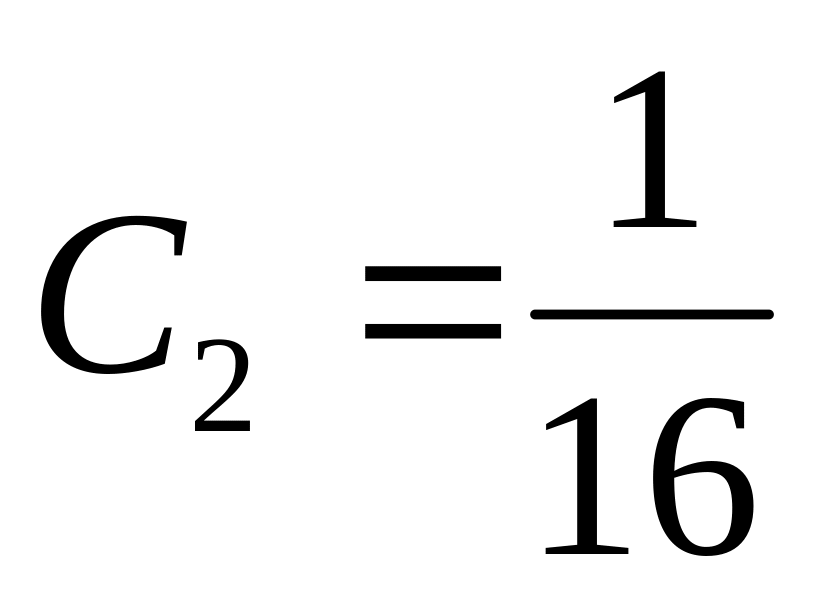 .
.
Пример данных к варианту №2
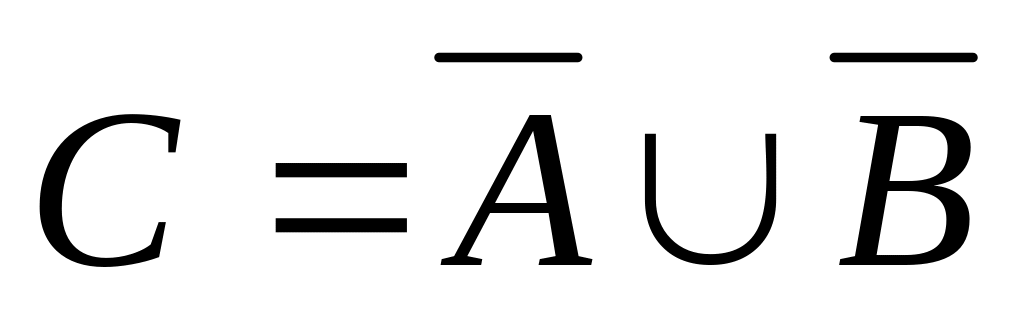 .
.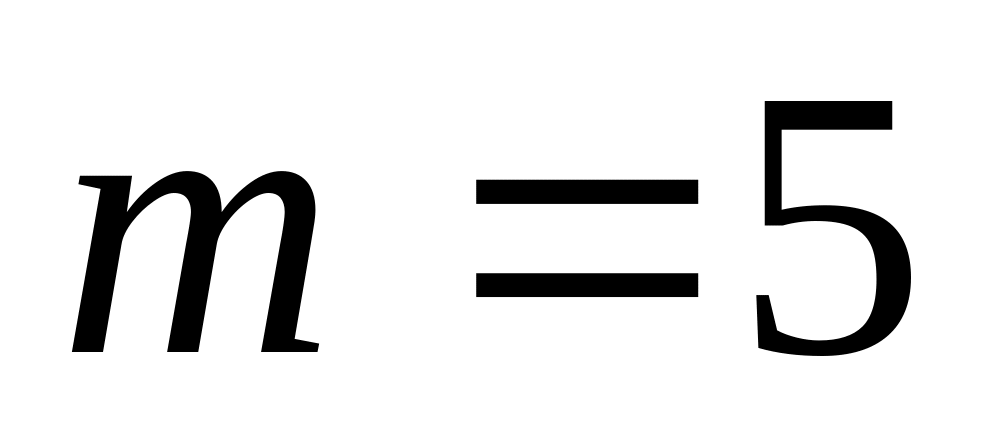 ,
,
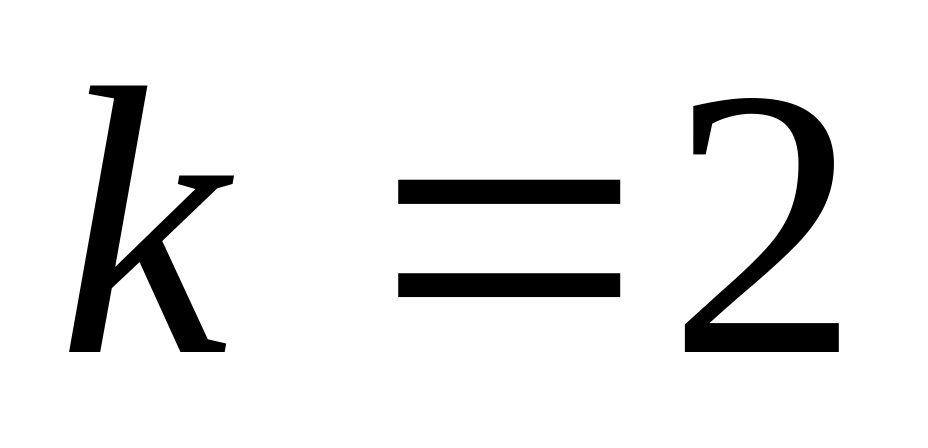 .
.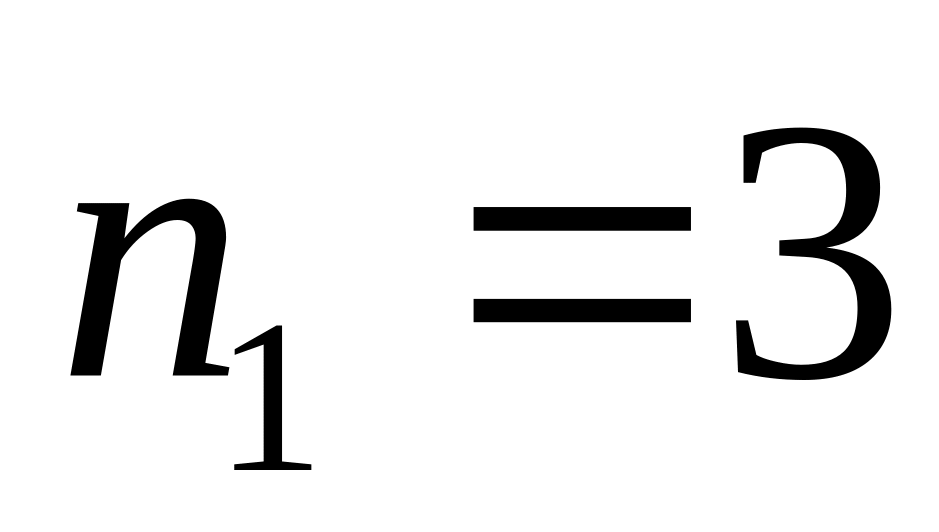 ,
,
,
,
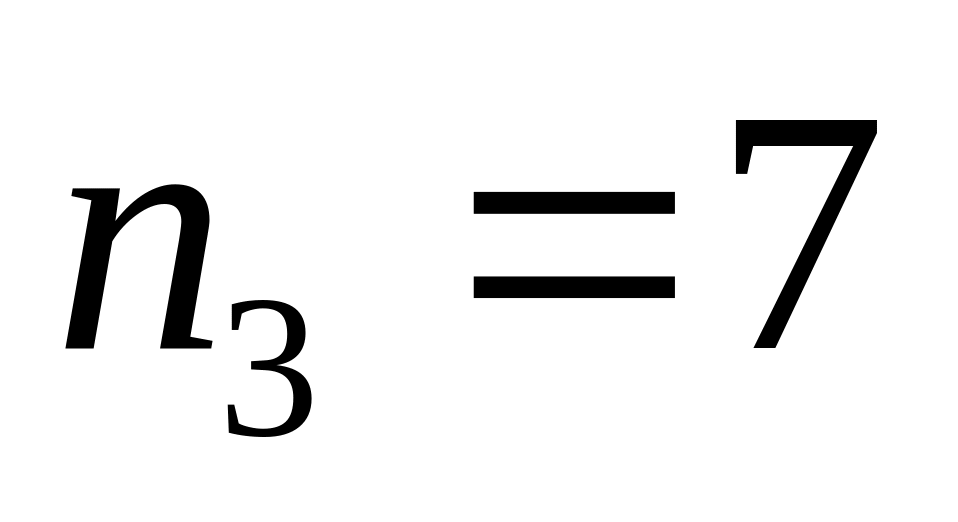 .
. ;
;
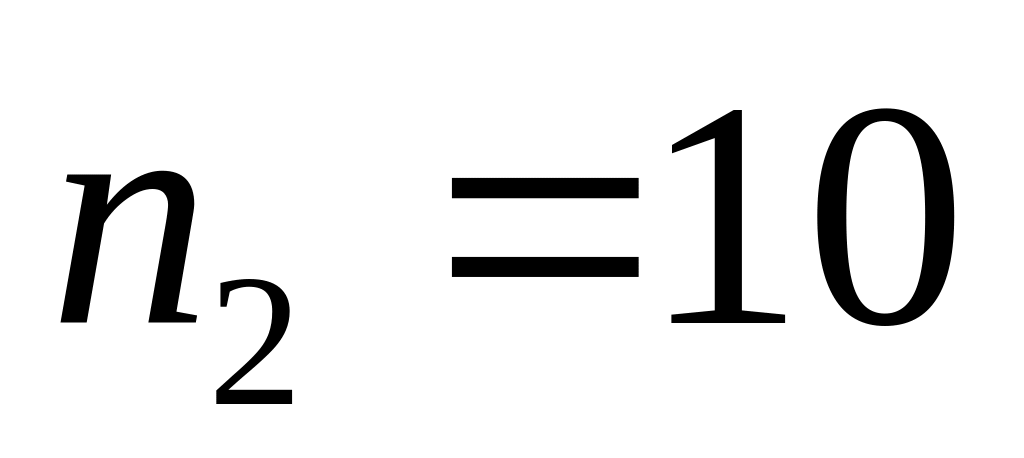 ;
;
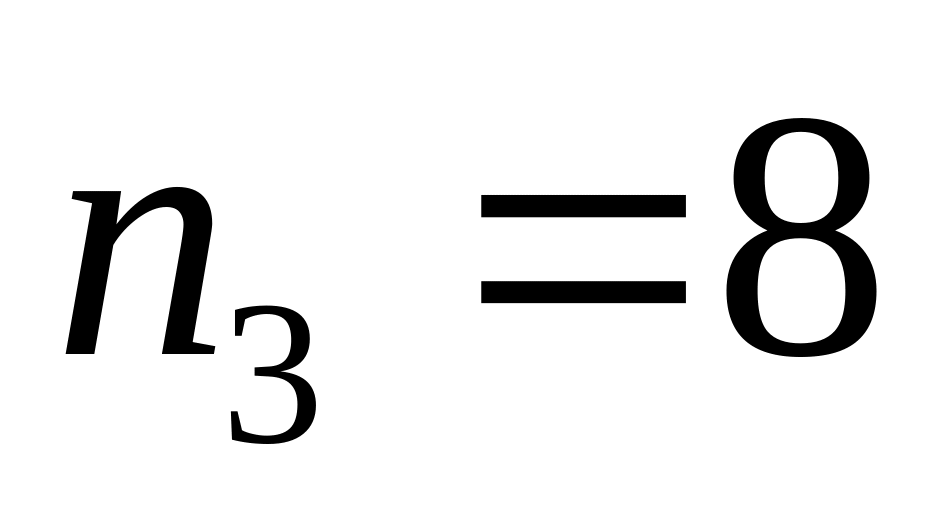 ;
;
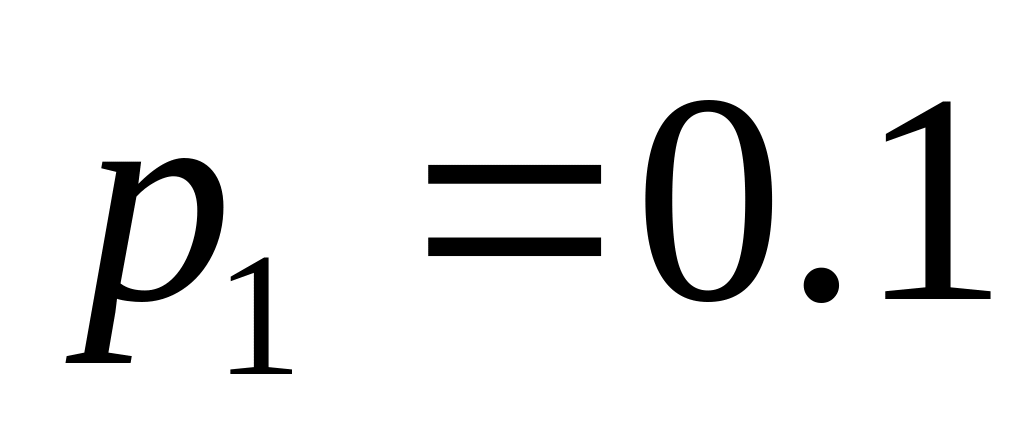 ;
;
 ;
;
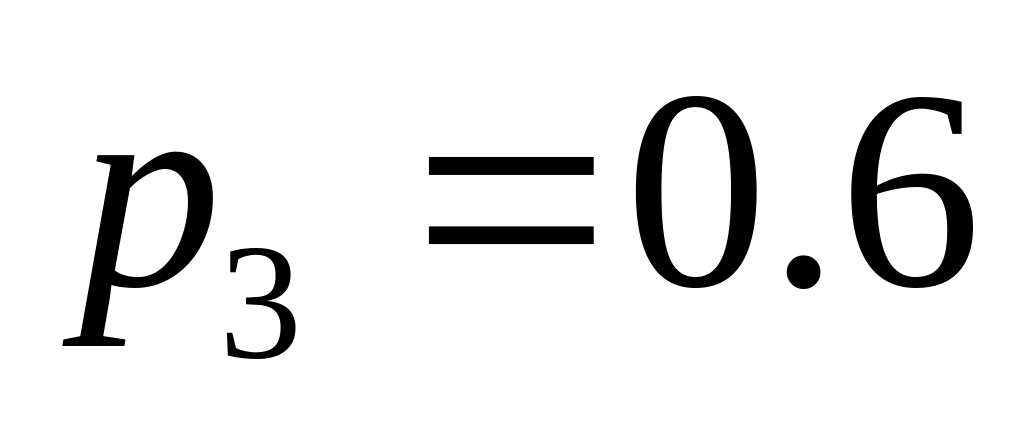 .
.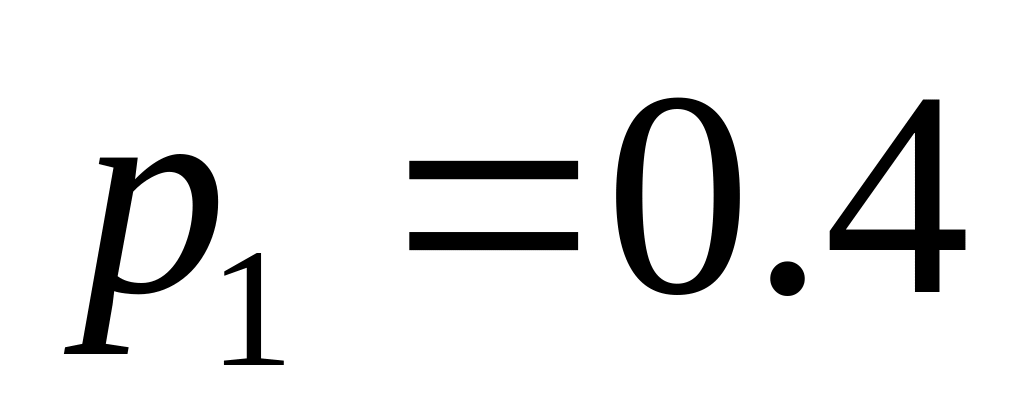 ;
;
.
;
;
. ,
,
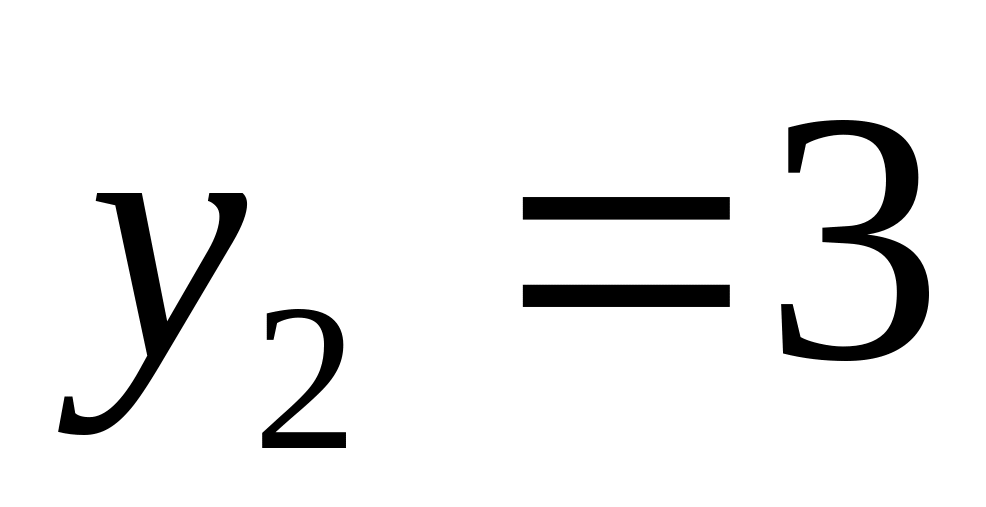 ,
,
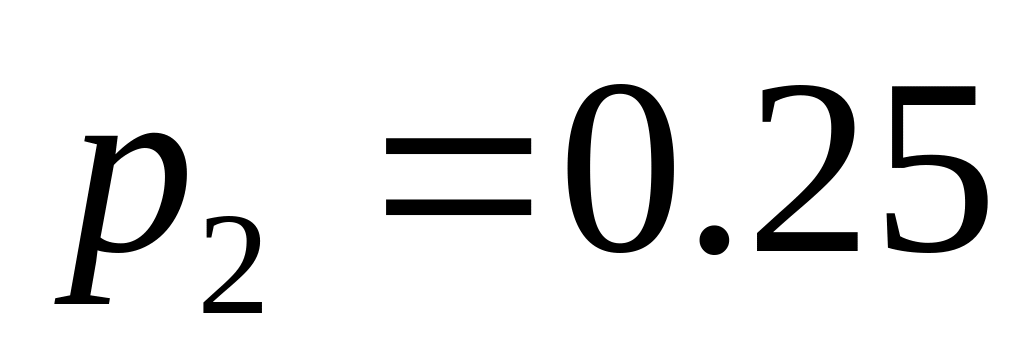 .
.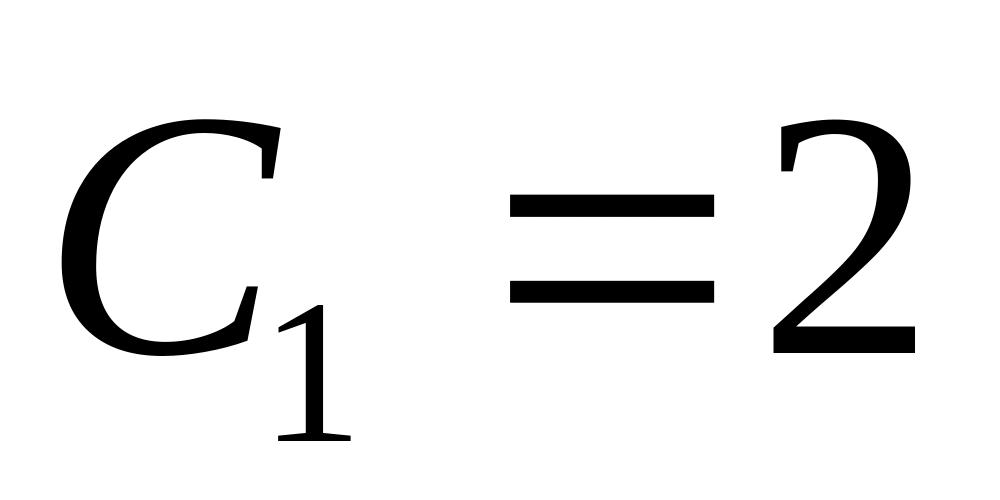 ,
,
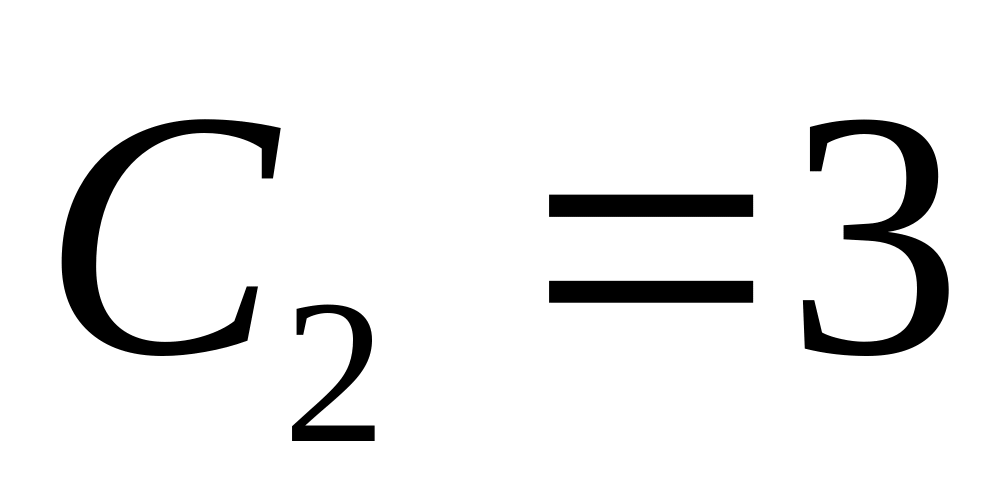 .
.
Пример данных к варианту №3
- {среди выбранных костей ровно один «дупель»}.
,
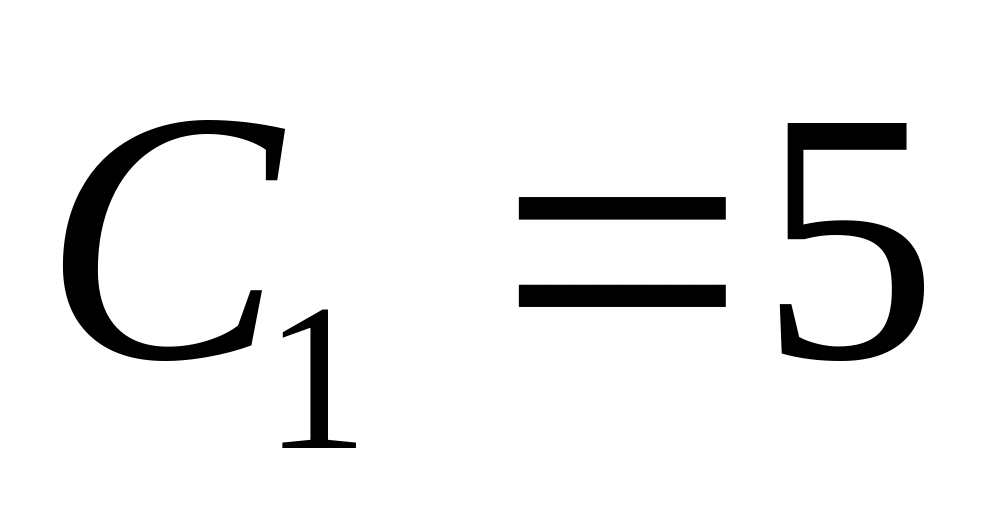 ,
.
,
.;
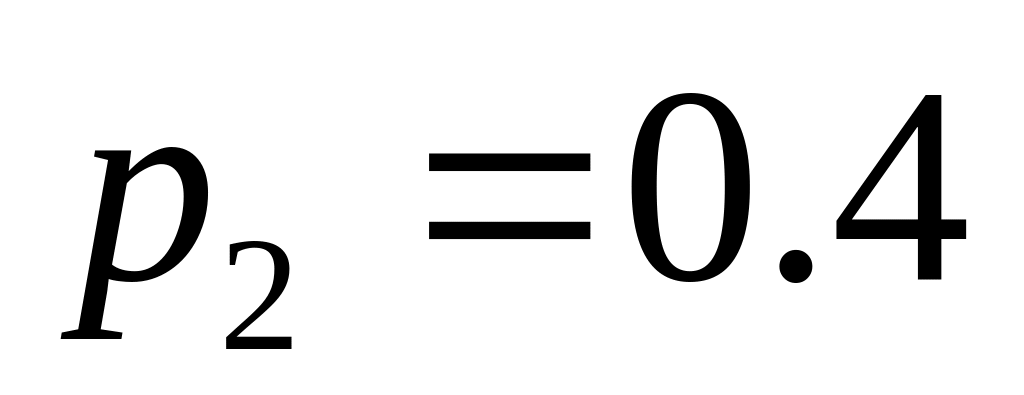 ;
;
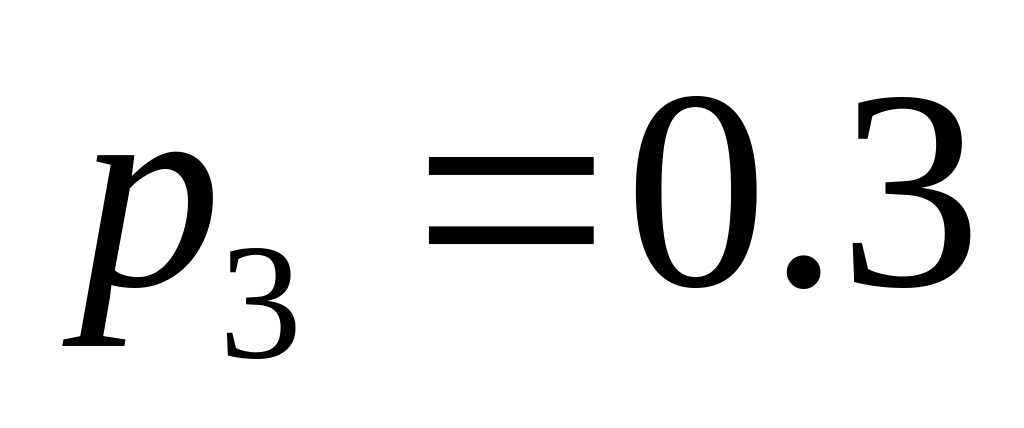 ;
;
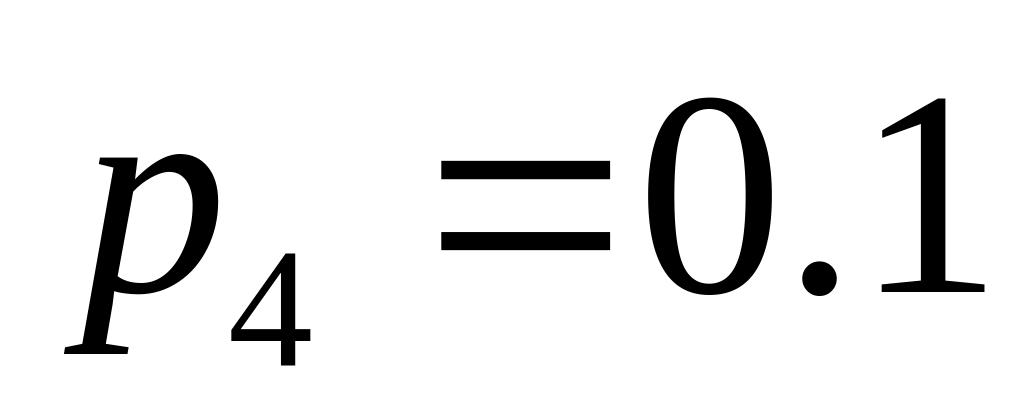 .
.;
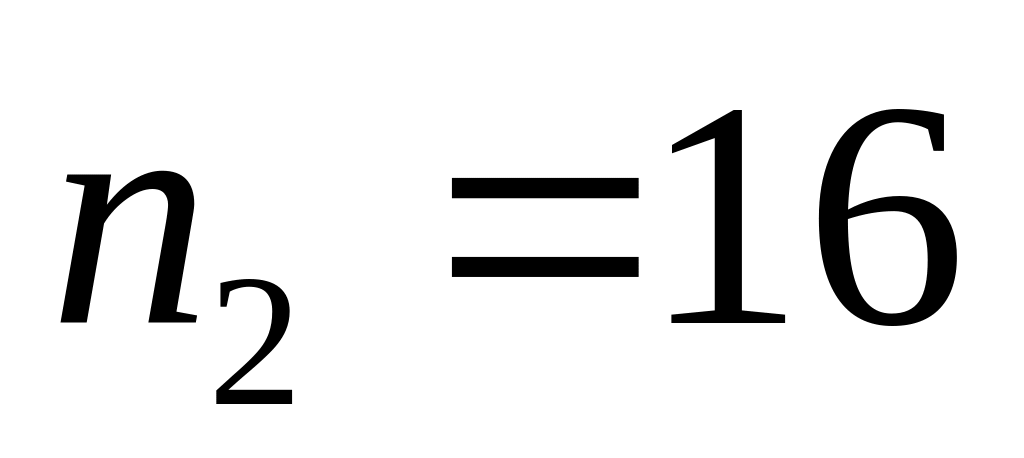 ;
;
.
;
;
.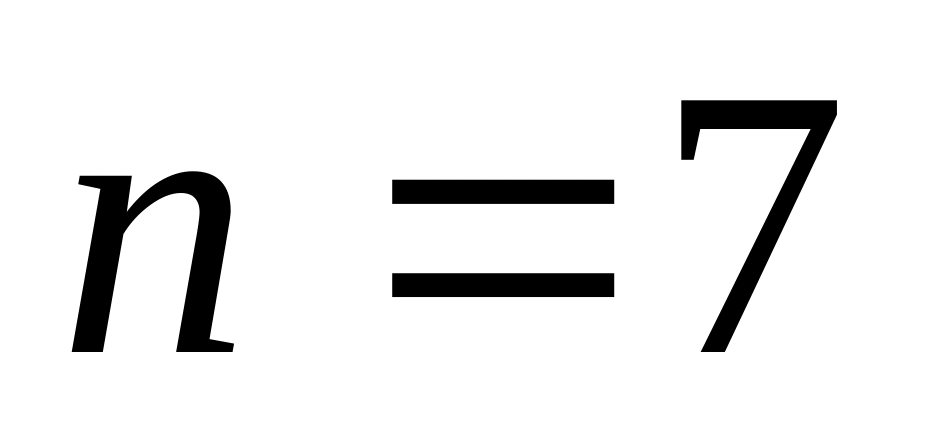 ,
.
,
.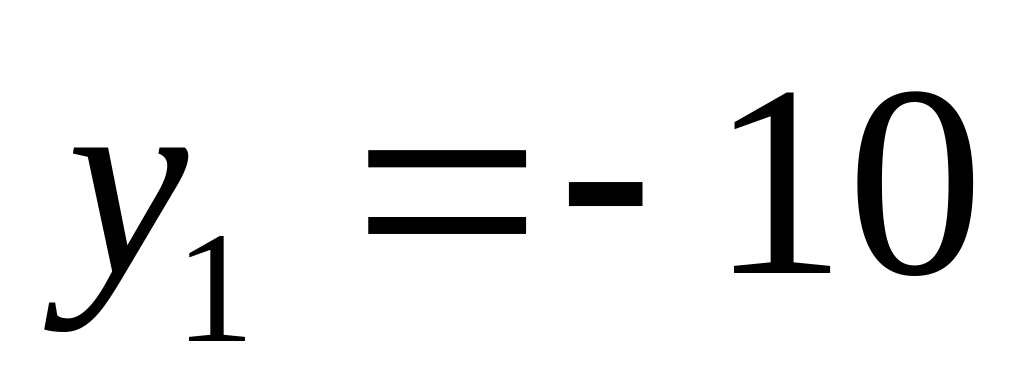 ;
;
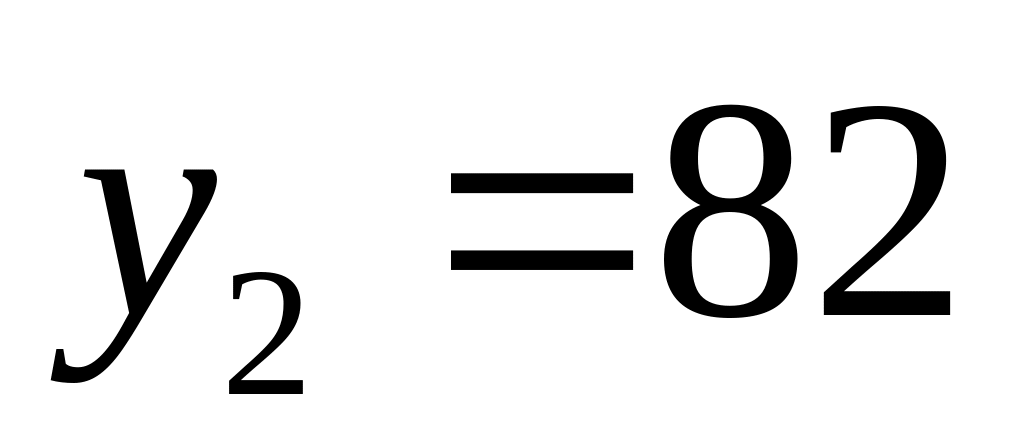 ;
;
;
;
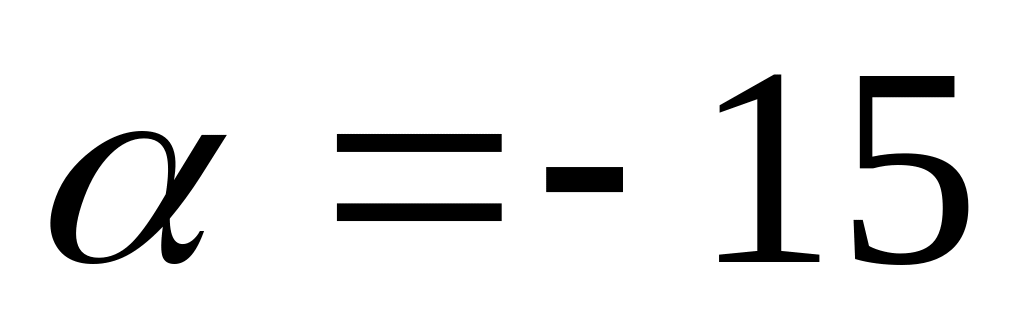 ;
;
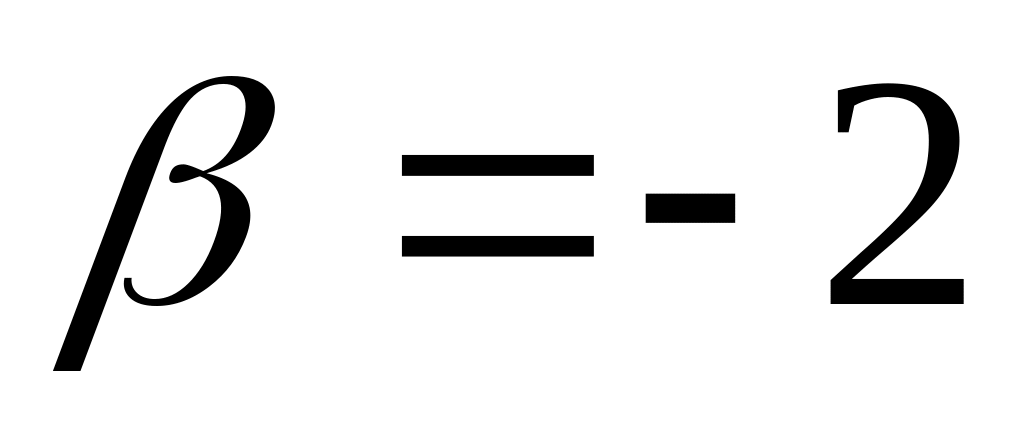 .
.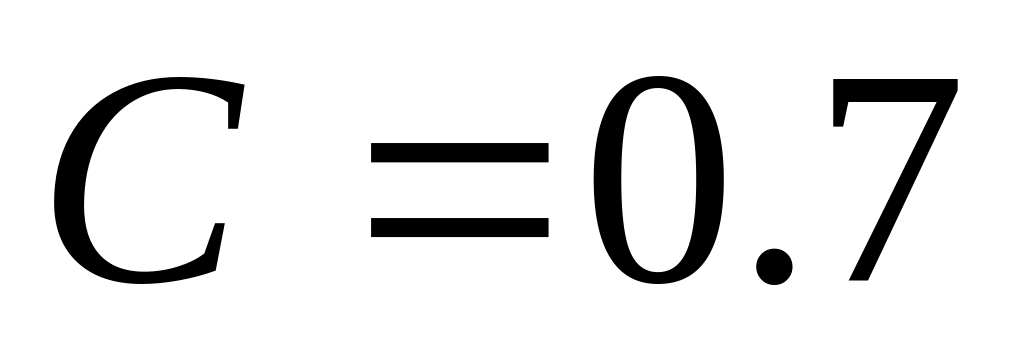 .
.
Пример данных к варианту №4
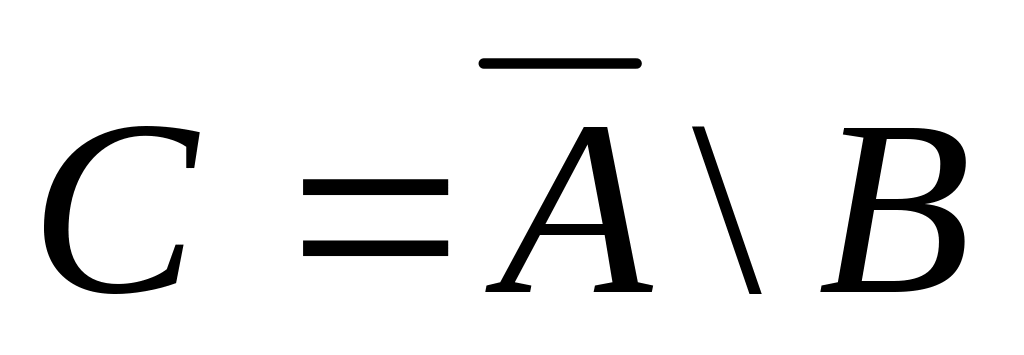 .
.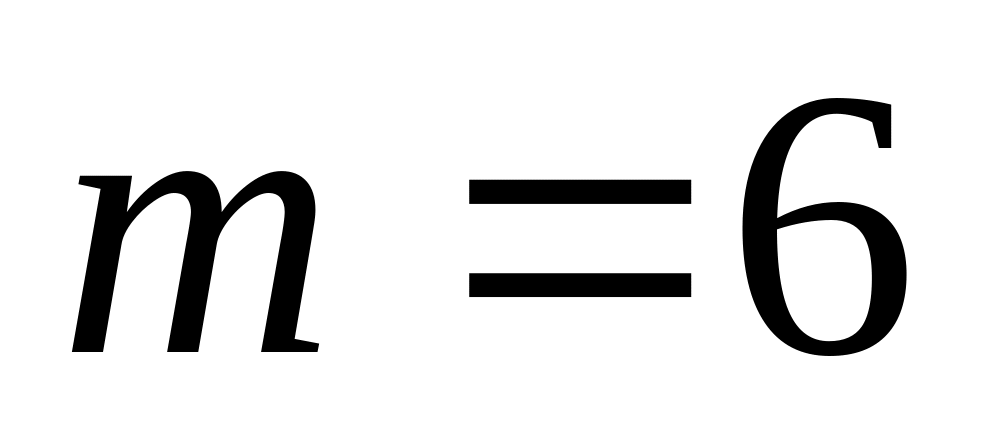 ,
.
,
.; ;
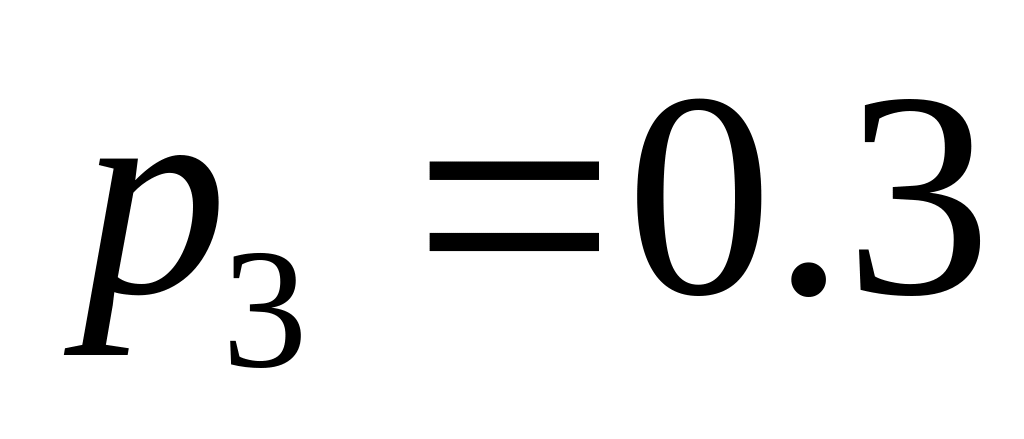 ;
;
.
;
;
. ,
,
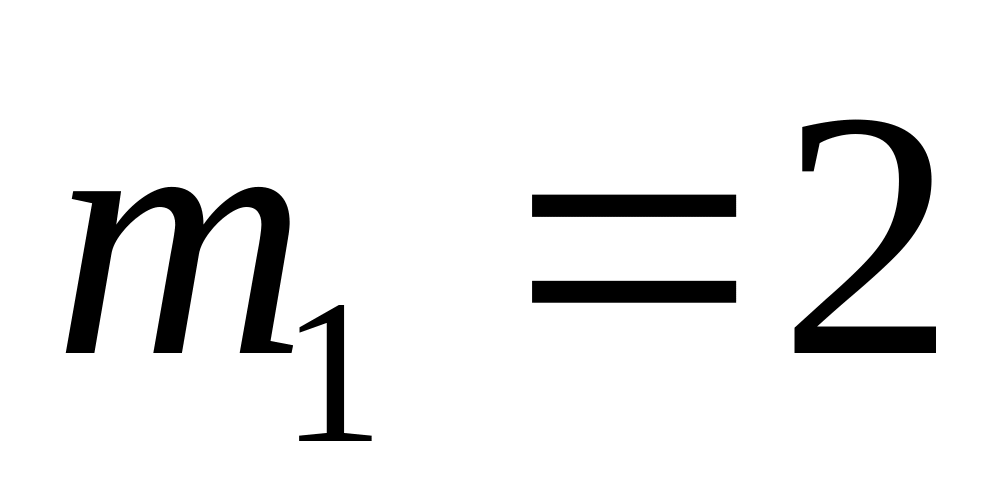 ,
,
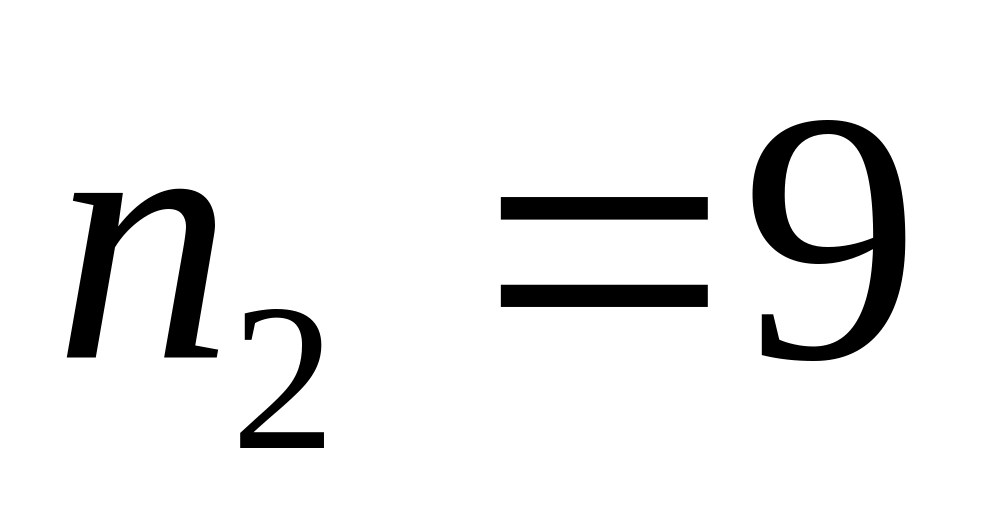 ,
,
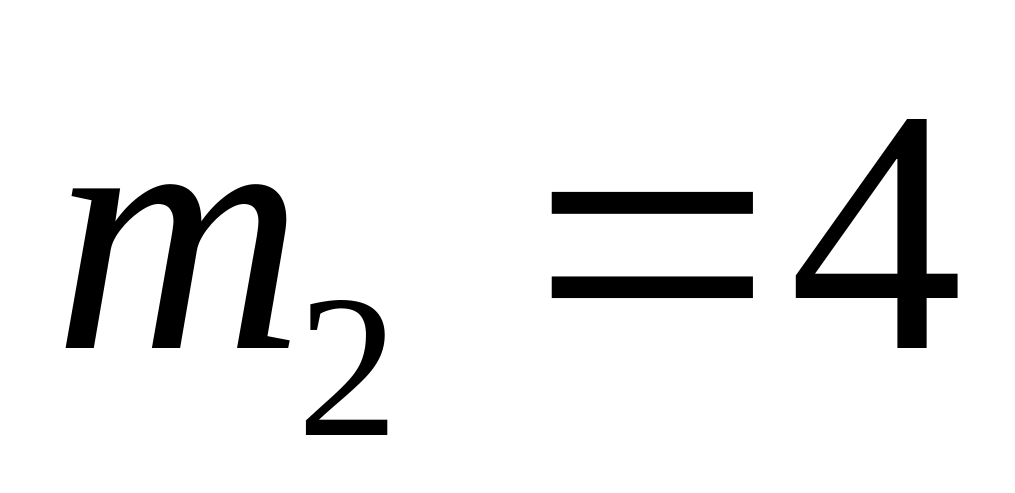 ,
,
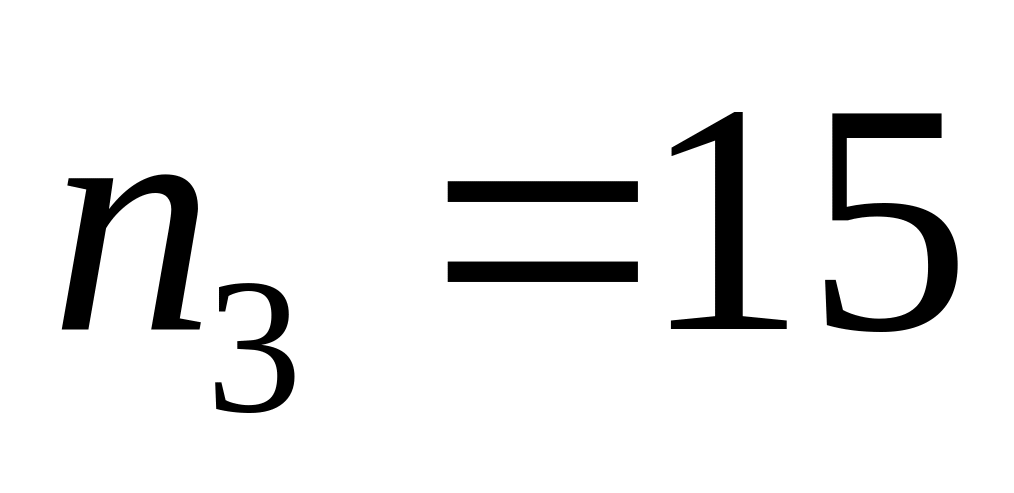 ,
,
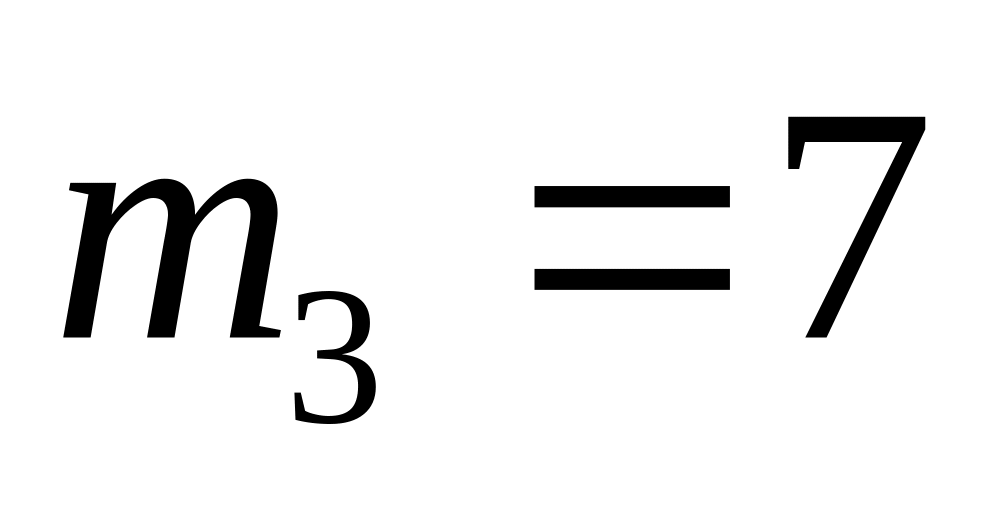 .
.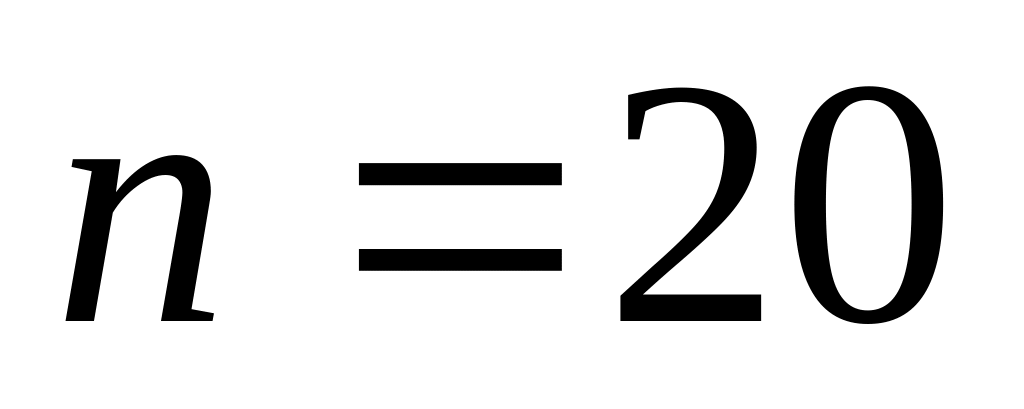 ,
,
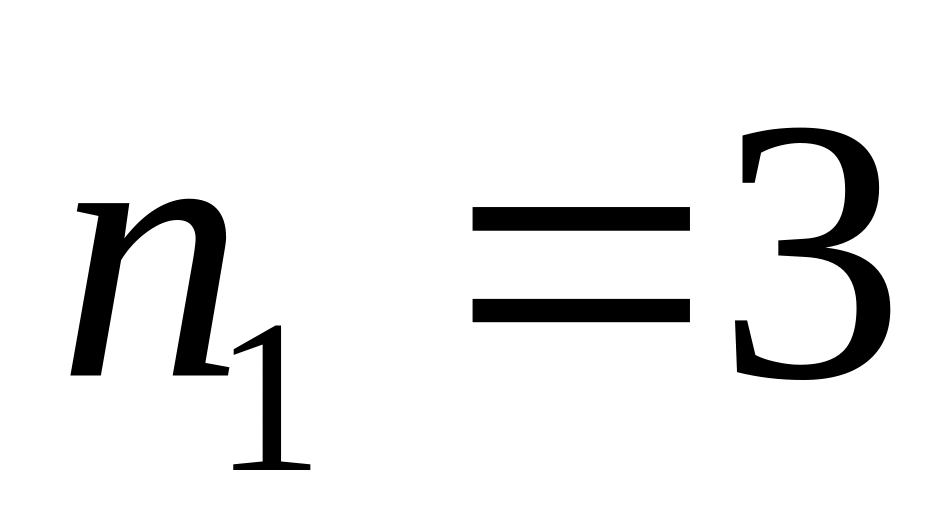 .
.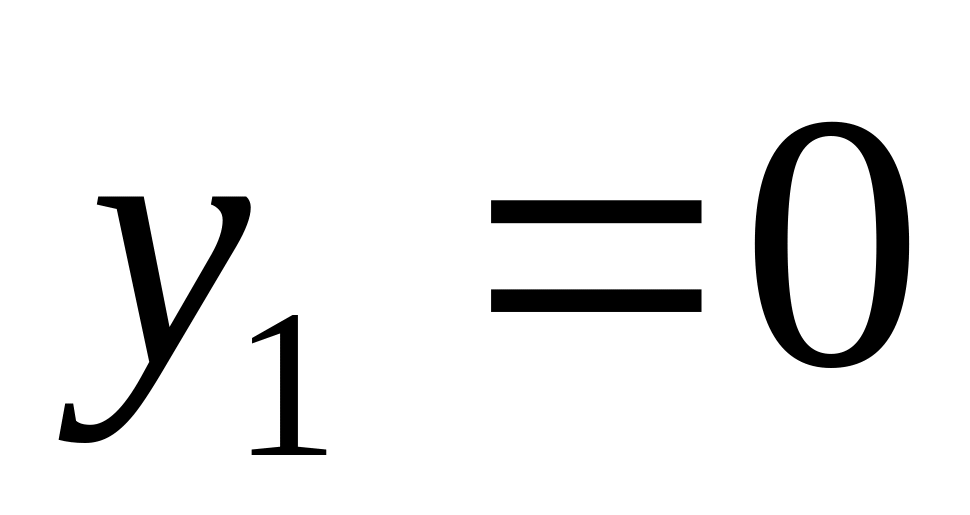 ;
;
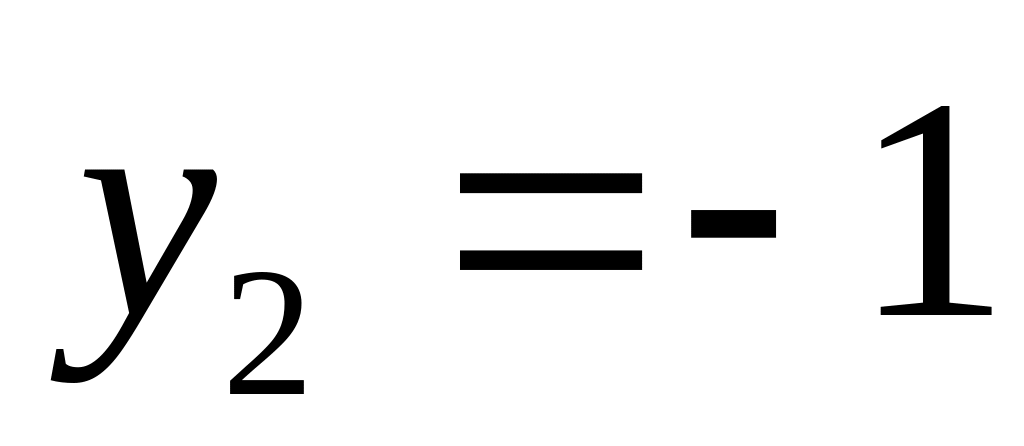 ;
;
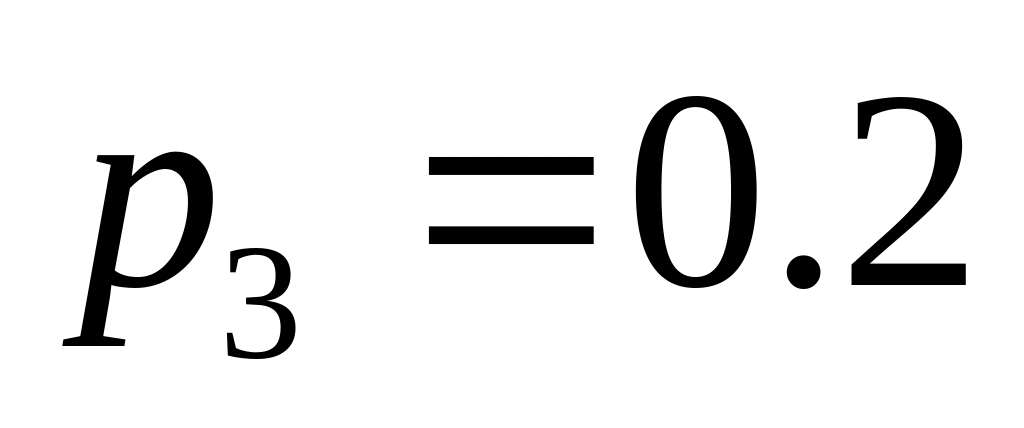 .
.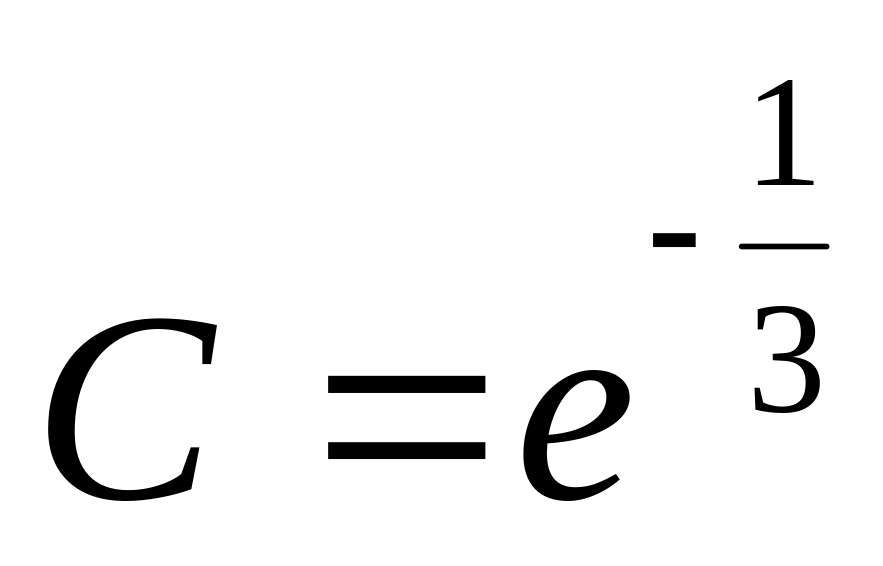 .
.
Пример данных к варианту №5
- {«шестёрка» не выпала ни разу}.
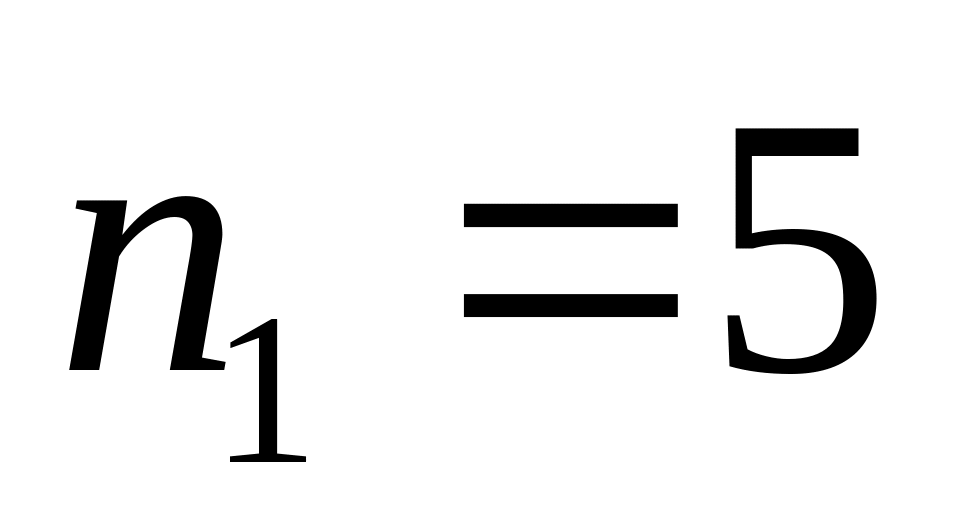 ,
,
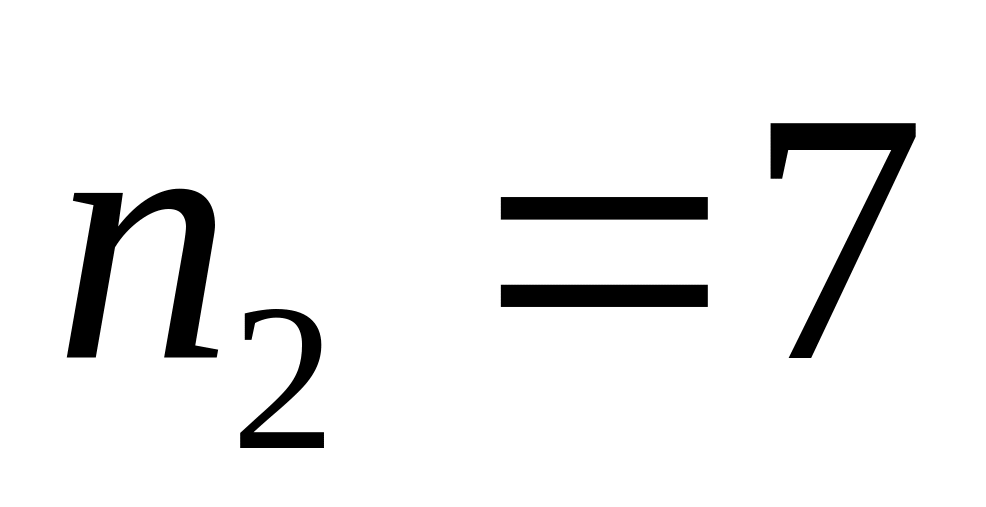 .
.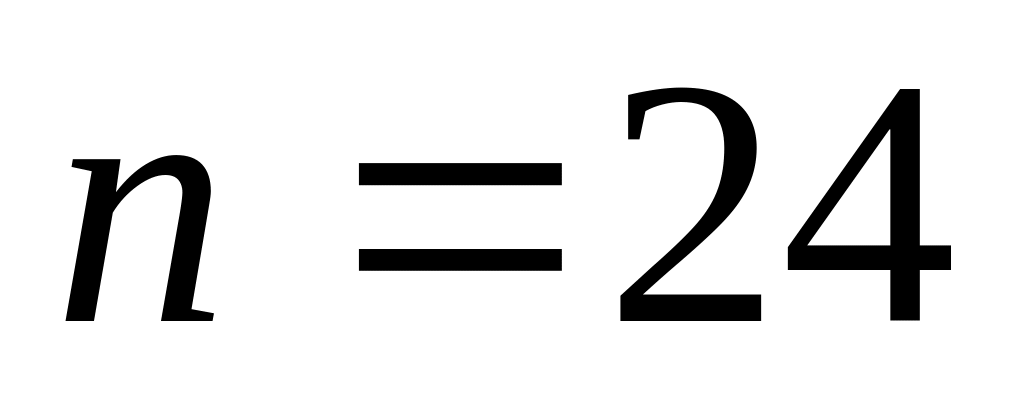 ,
,
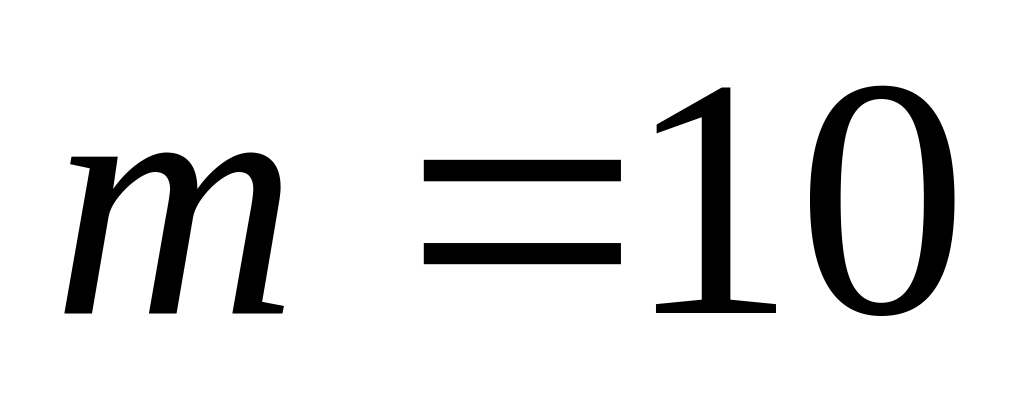 .
.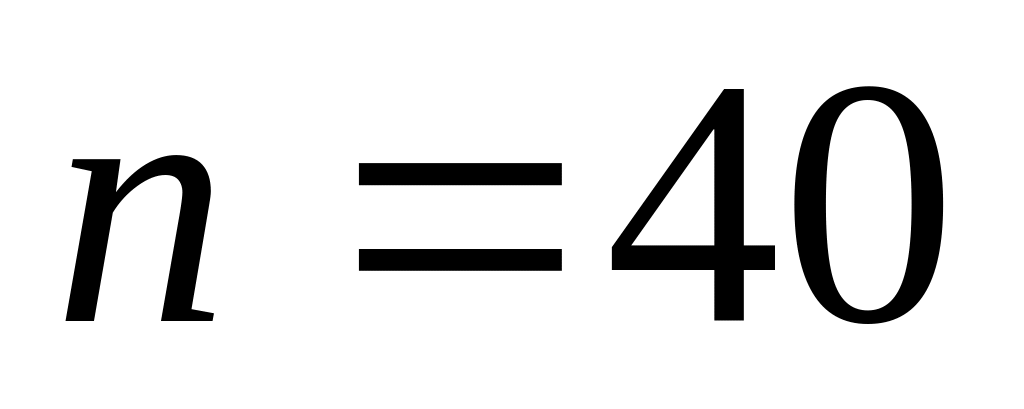 ;
;
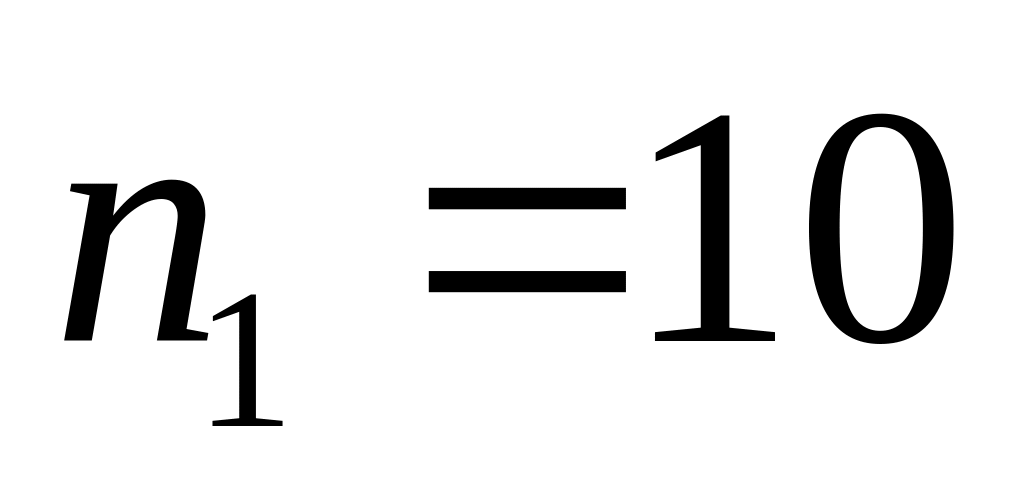 ;
;
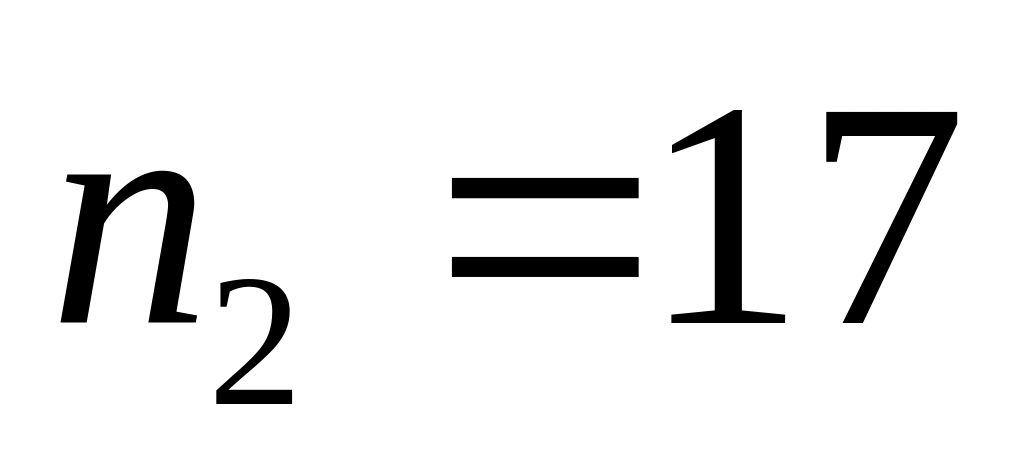 ;
;
;
;
;
;
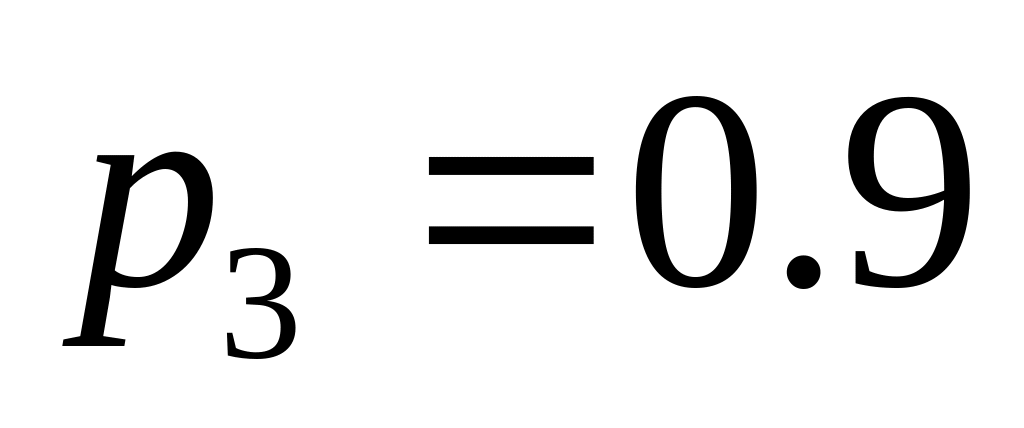 .
.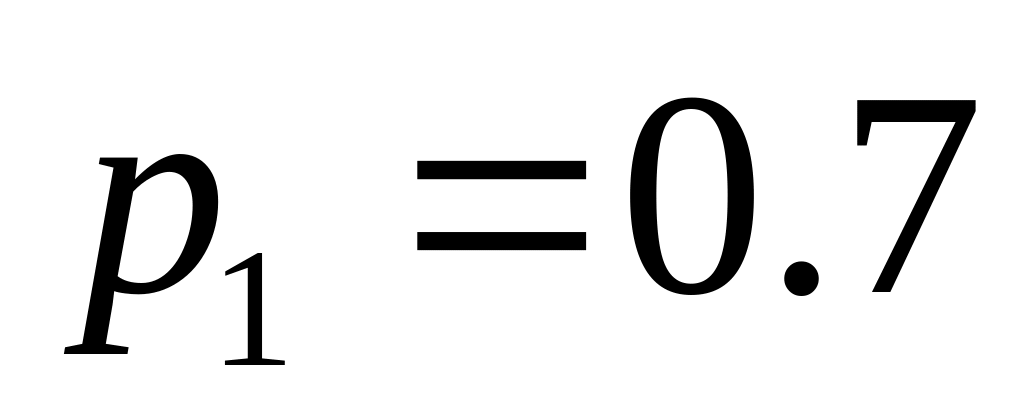 ;
;
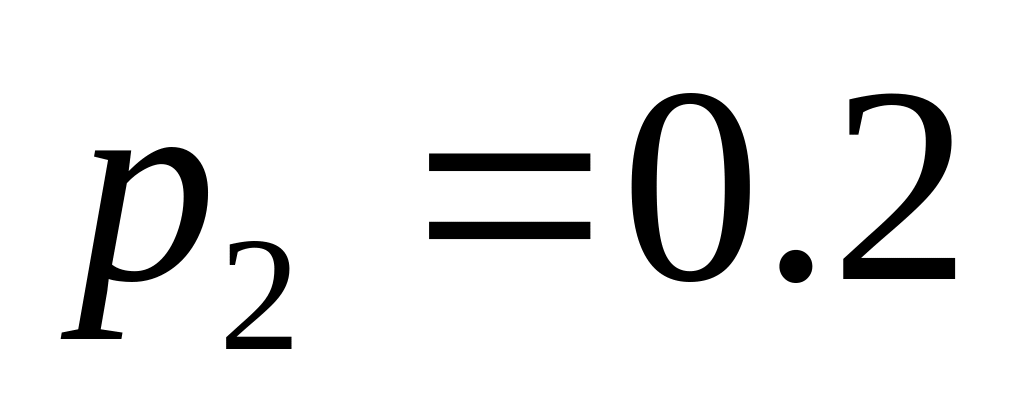 ;
;
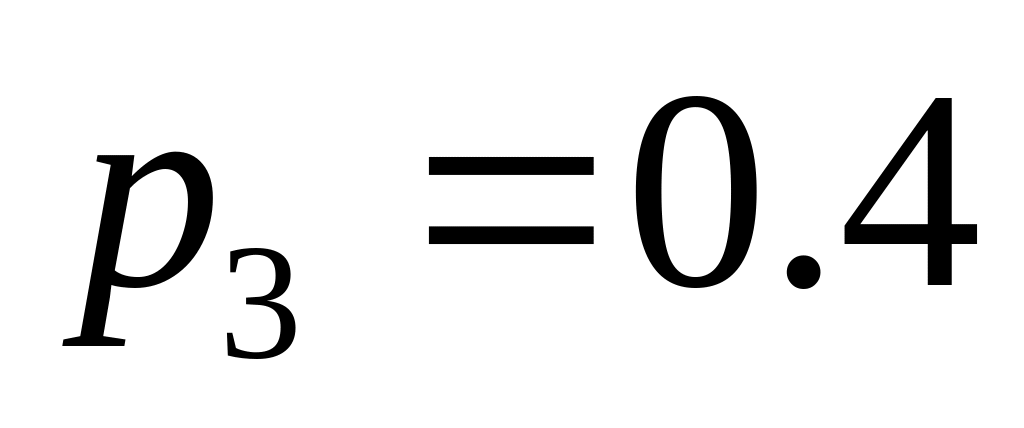 .
.,
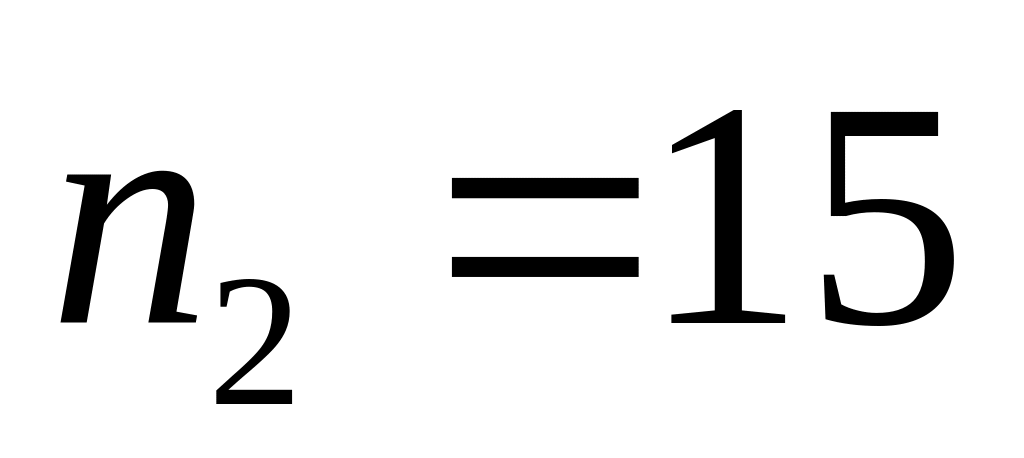 ,
,
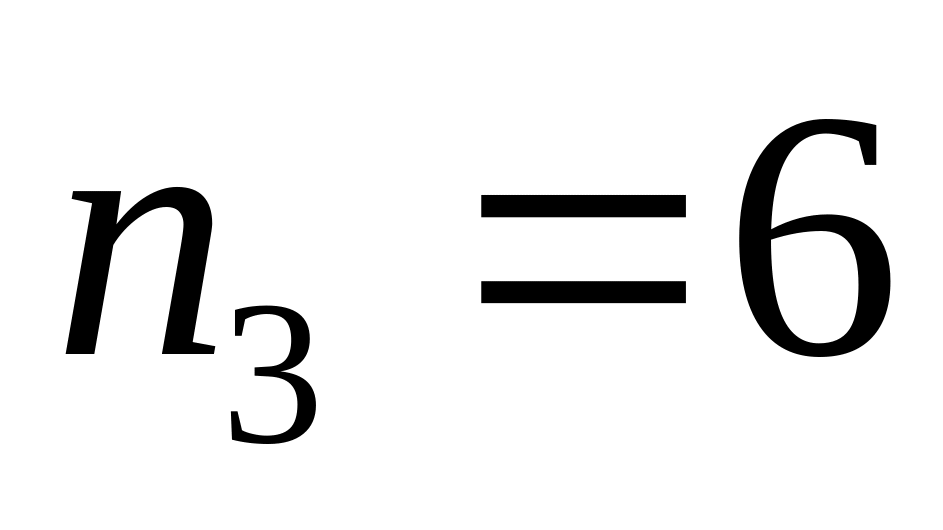 .
.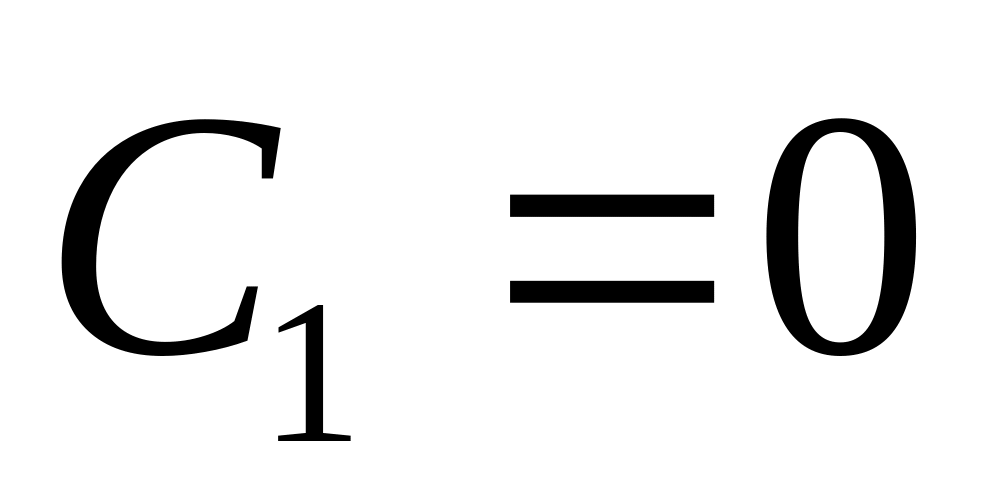 ,
,
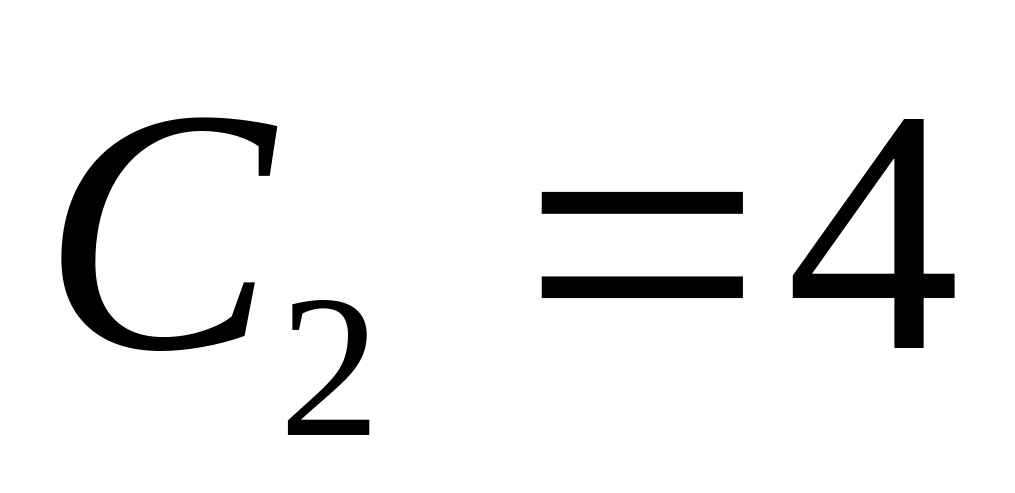 .
.
Пример данных к варианту №6
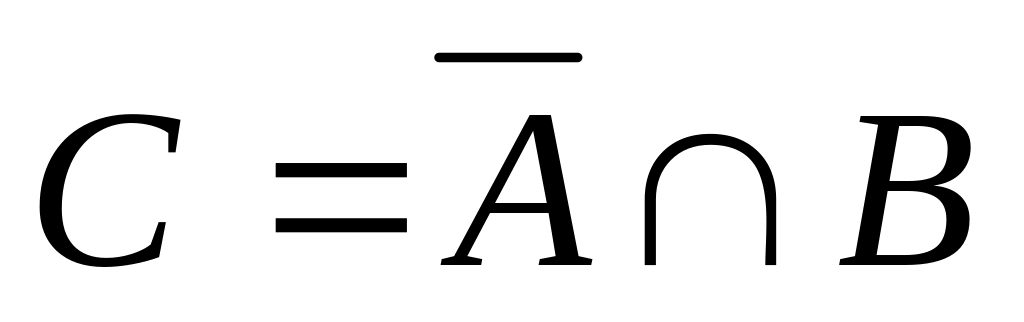 .
.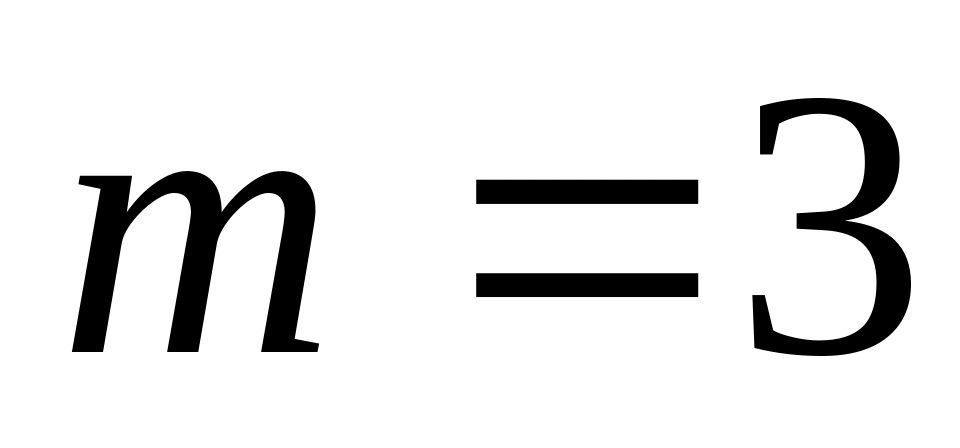 ,
.
,
.;
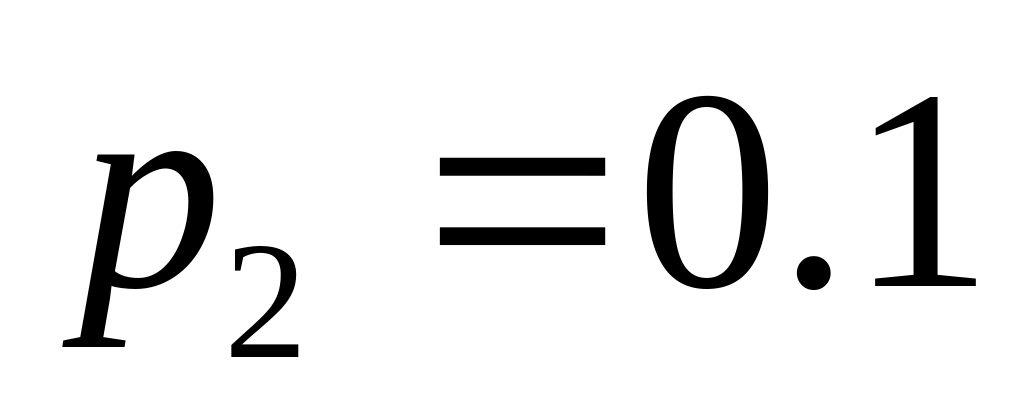 ;
;
.
;
;
.,
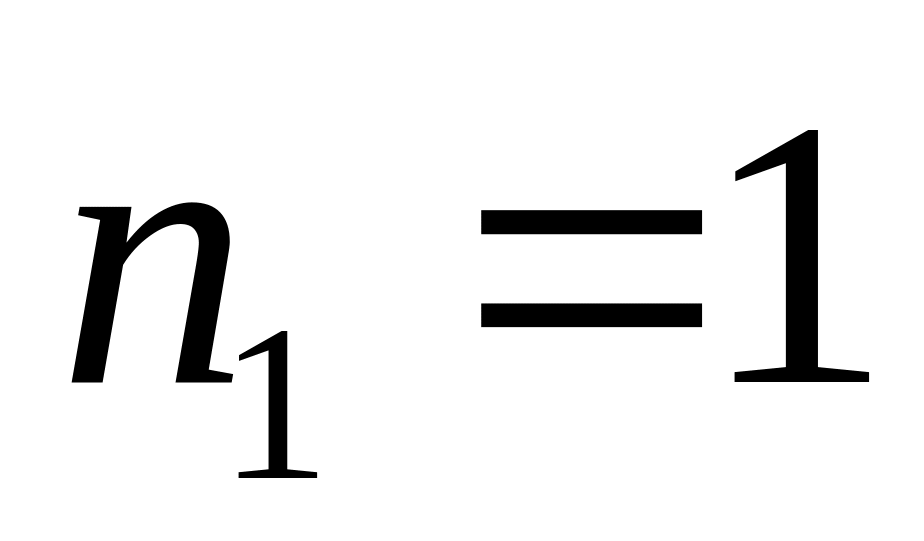 ,
,
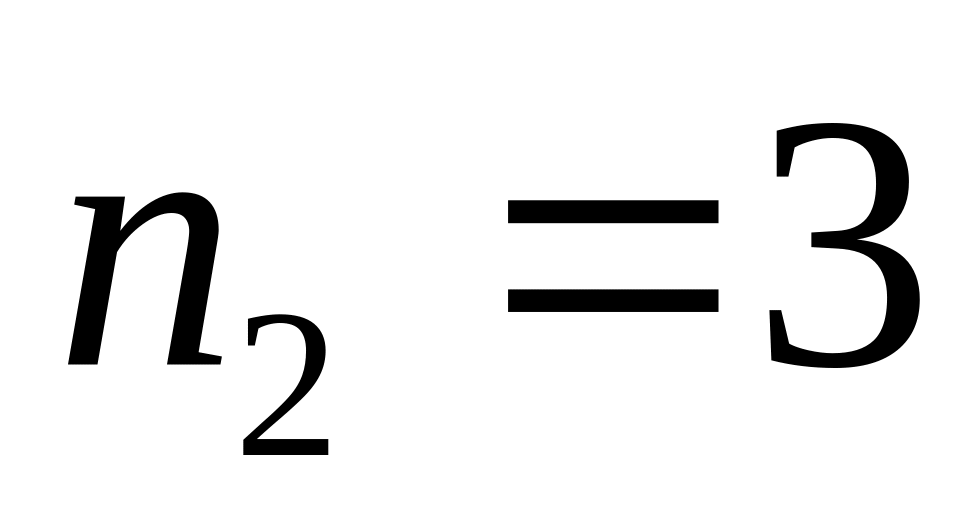 ,
,
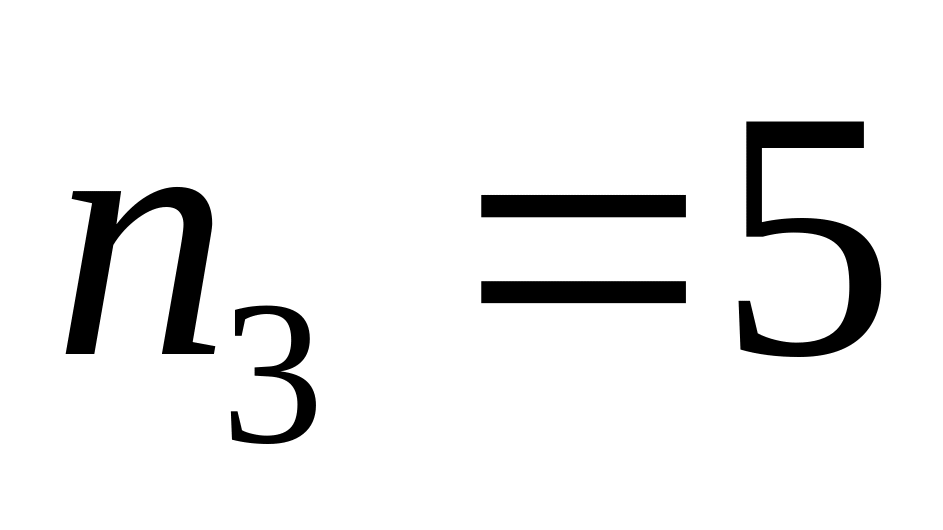 .
.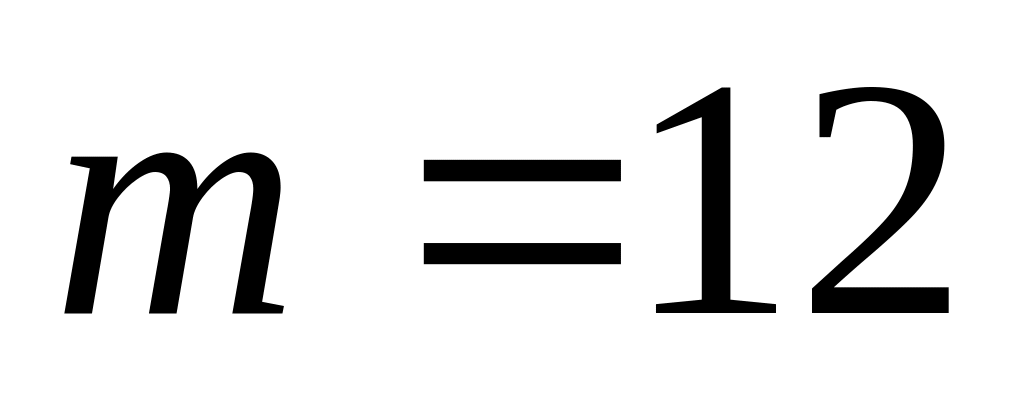 ,
,
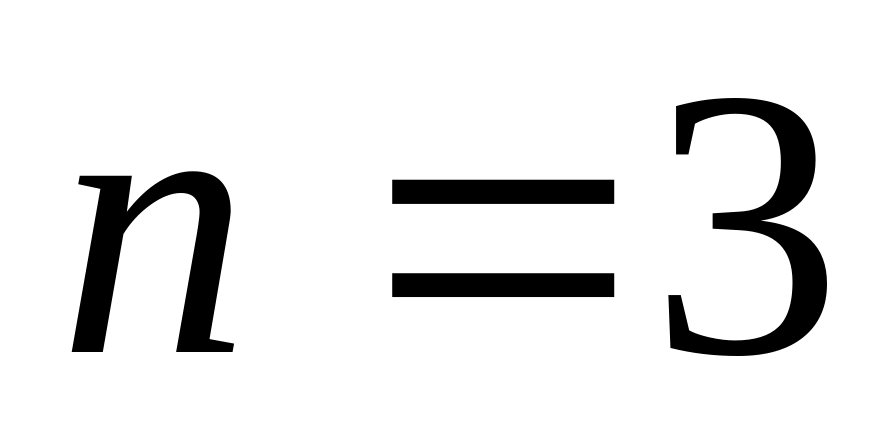 .
.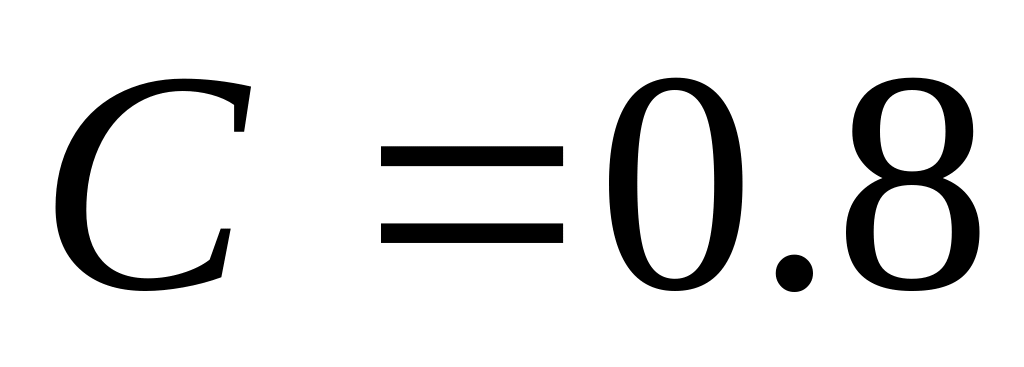 ;
.
;
.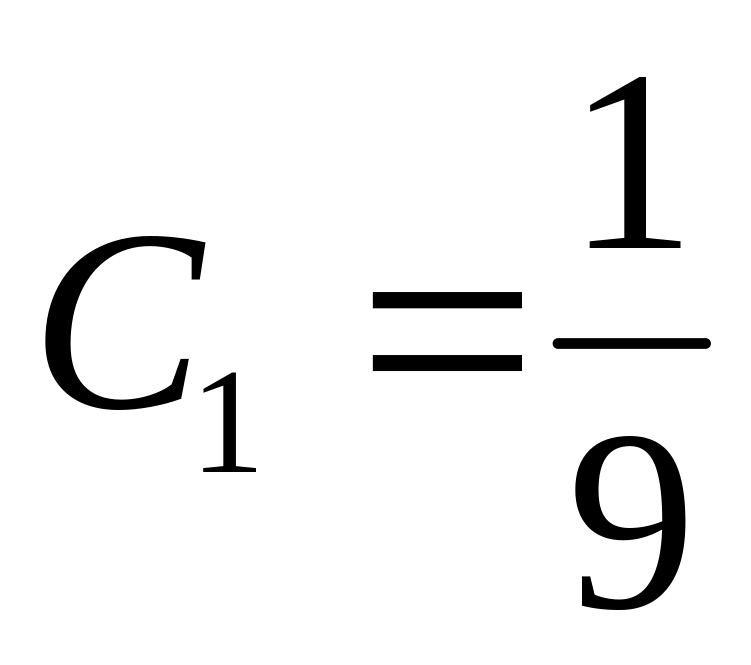 ,
,
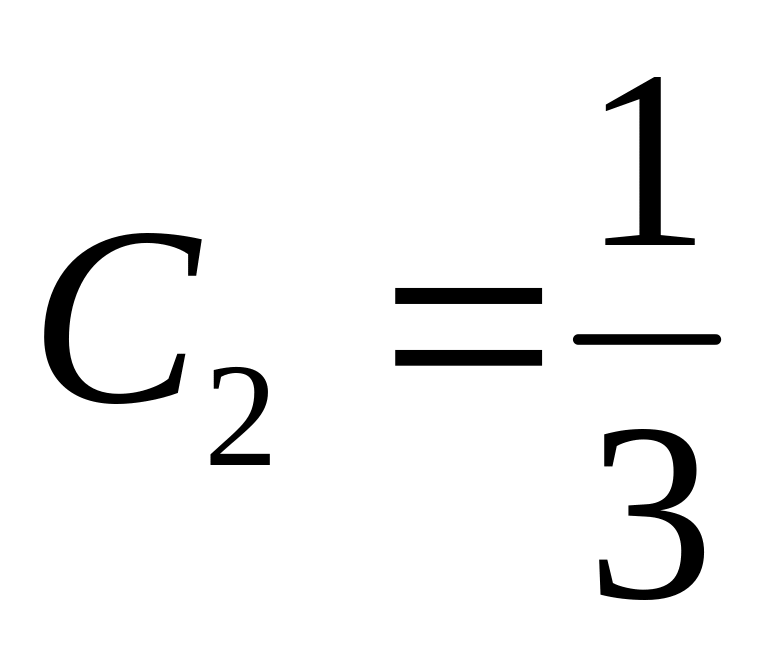 .
.
Пример данных к варианту №7
- {вышел из строя только второй прибор}.
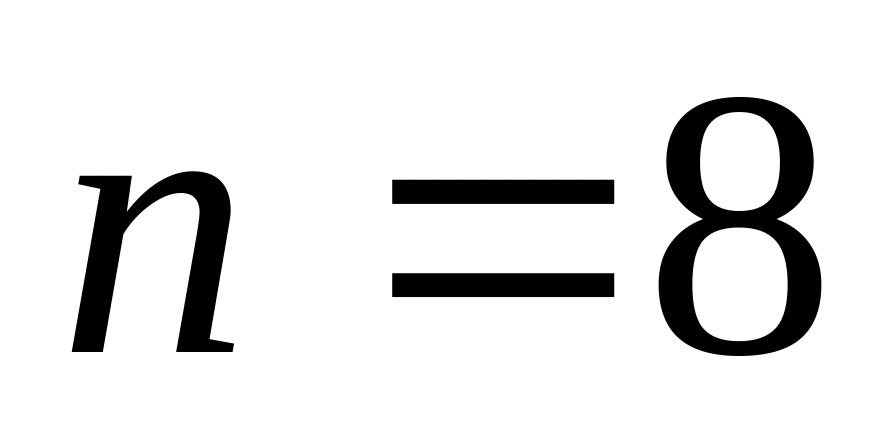 ,
,
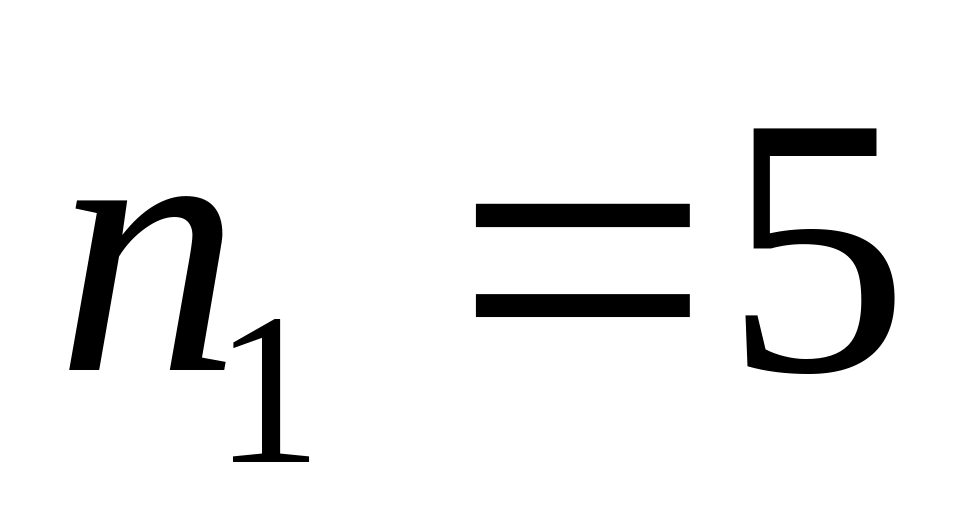 .
.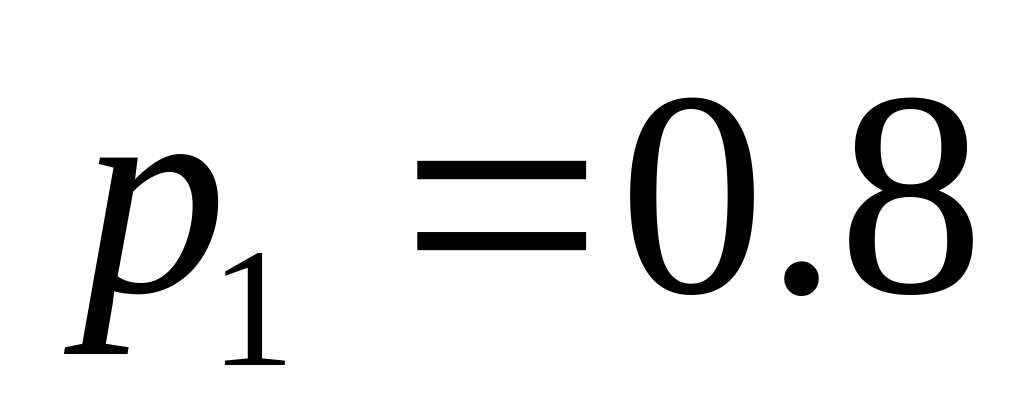 ;
;
;
.
;
;
;
.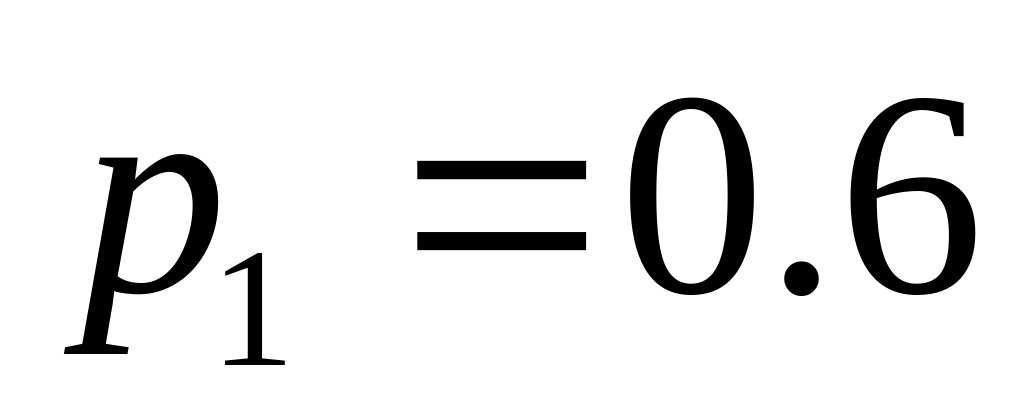 ;
;
;
;
;
;
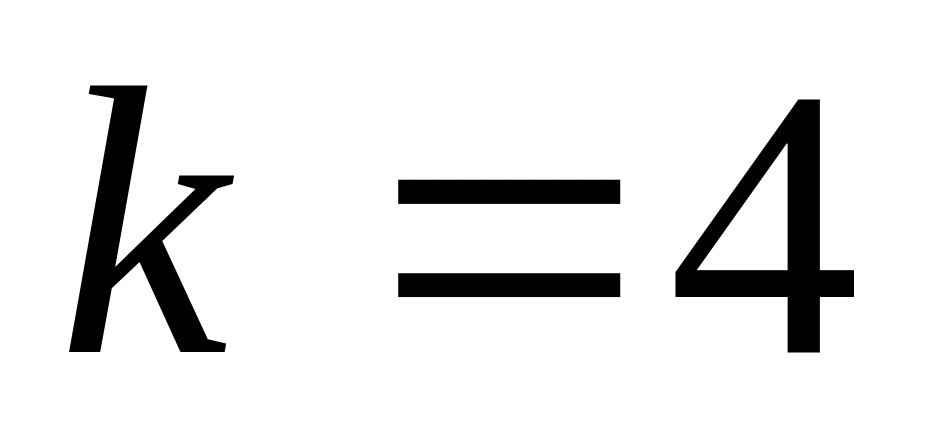 .
., .
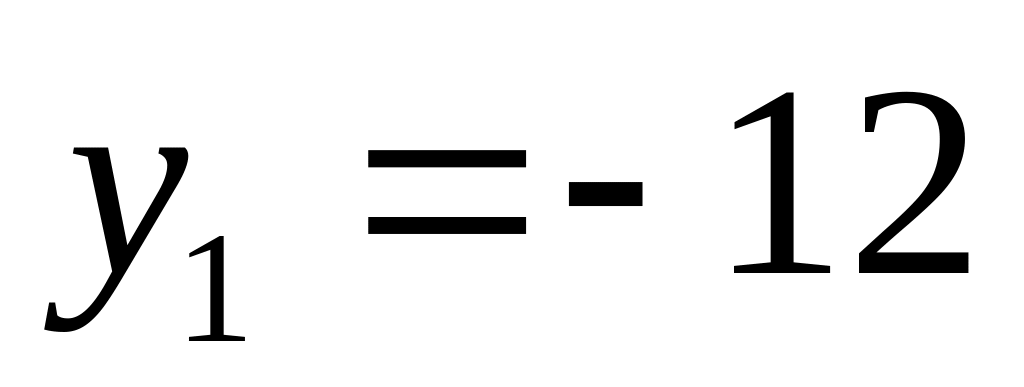 ;
;
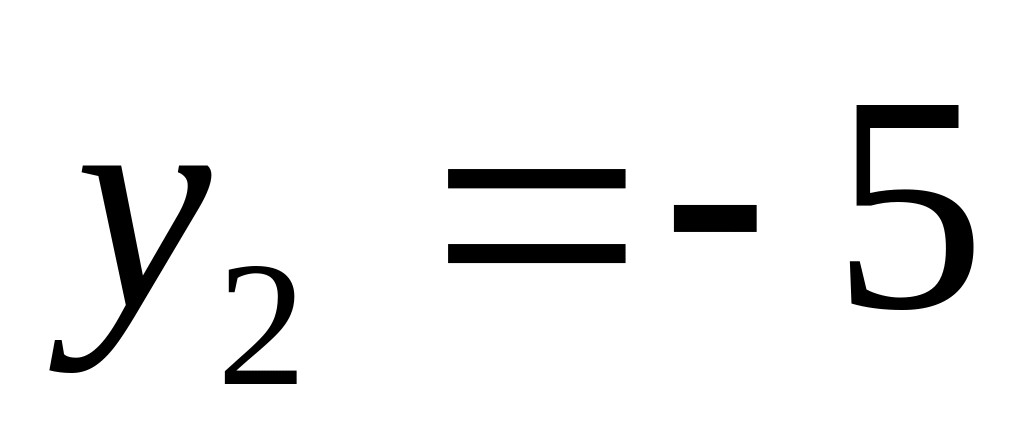 ;
;
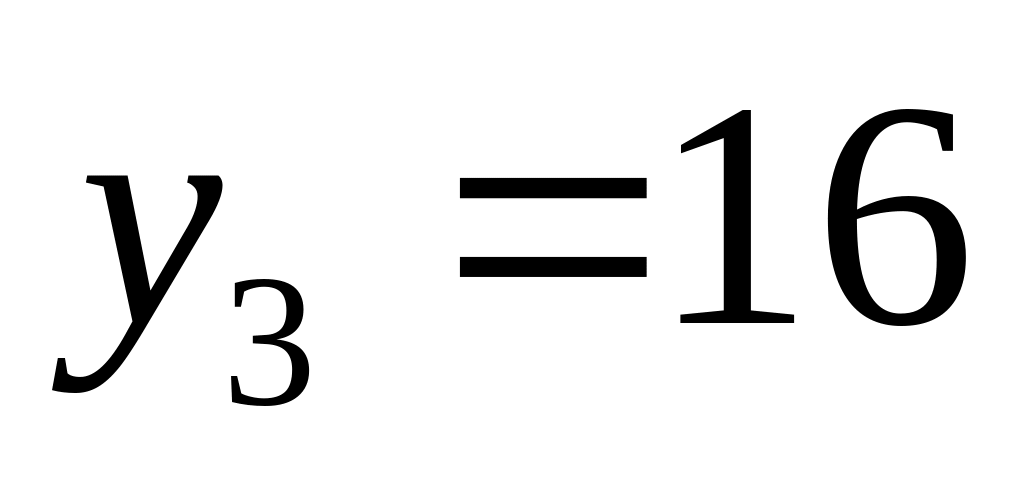 ;
;
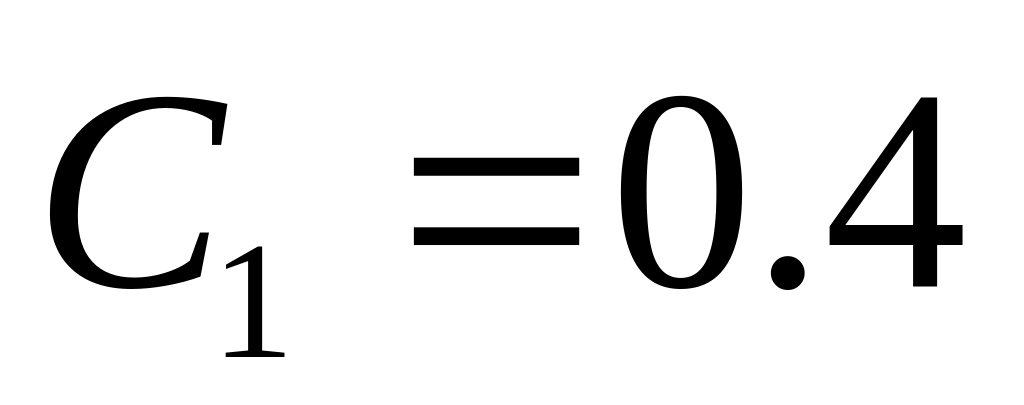 ;
;
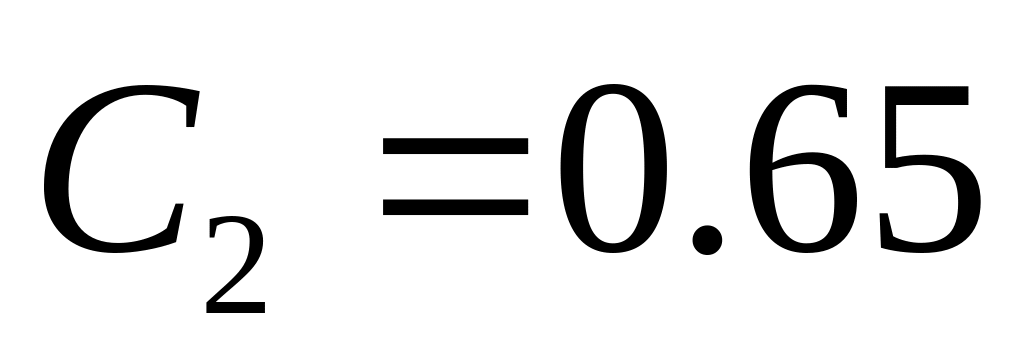 .
.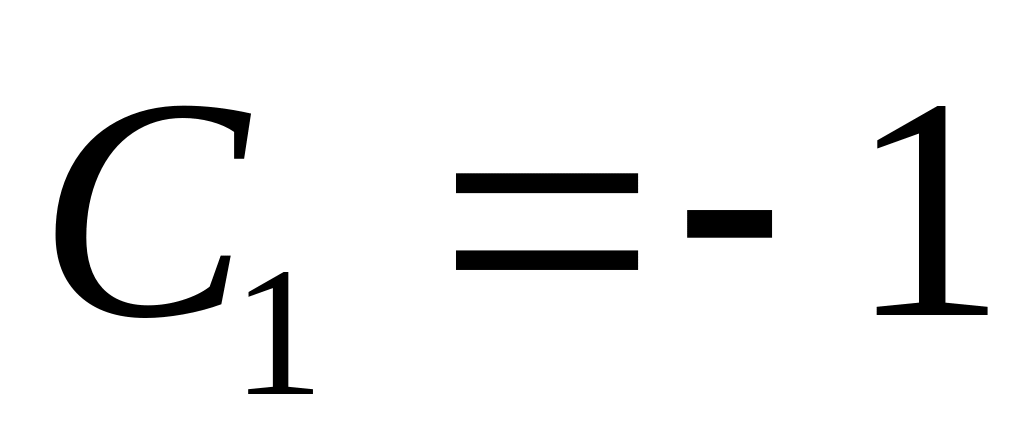 ,
,
 .
.
Пример данных к варианту №8
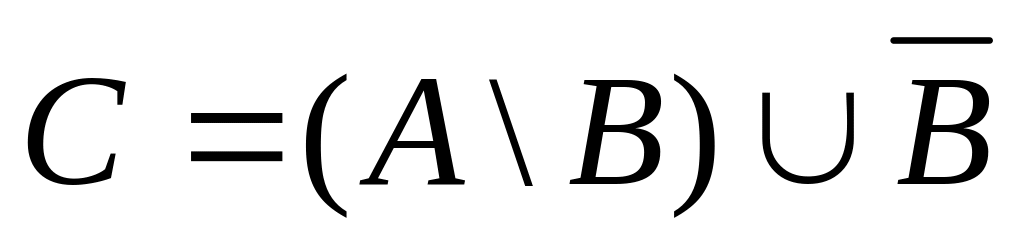 .
.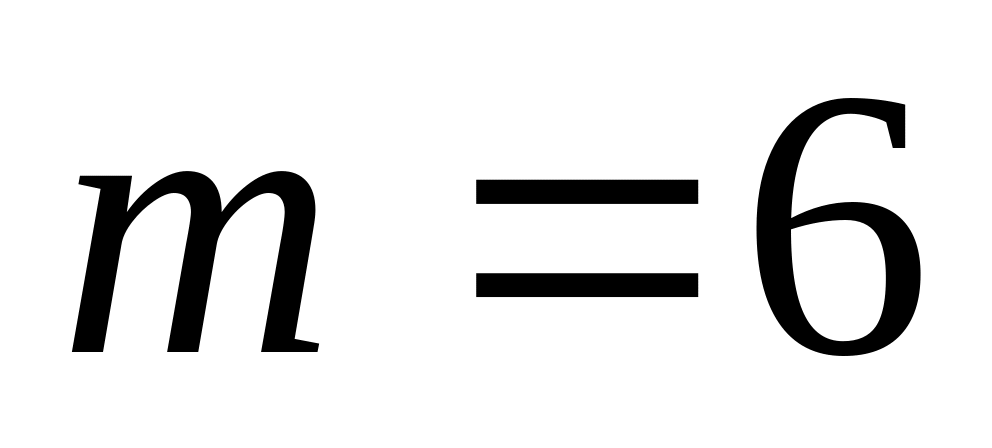 ,
.
,
.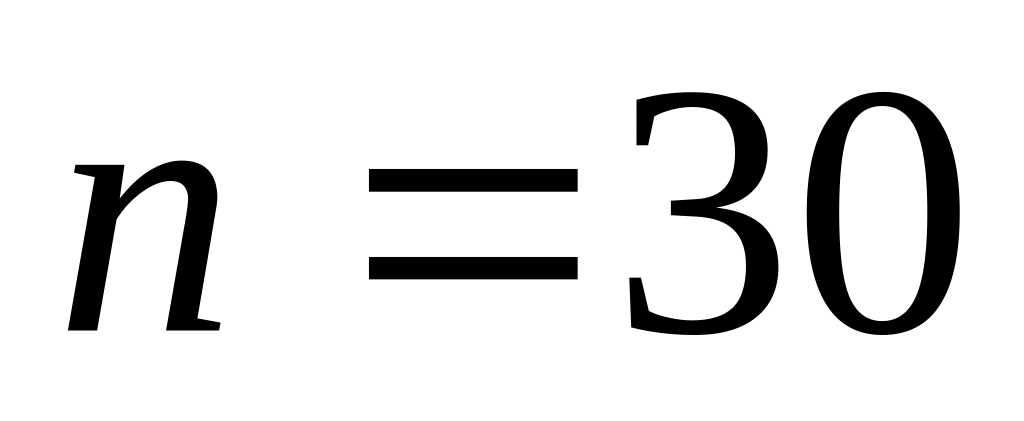 ,
,
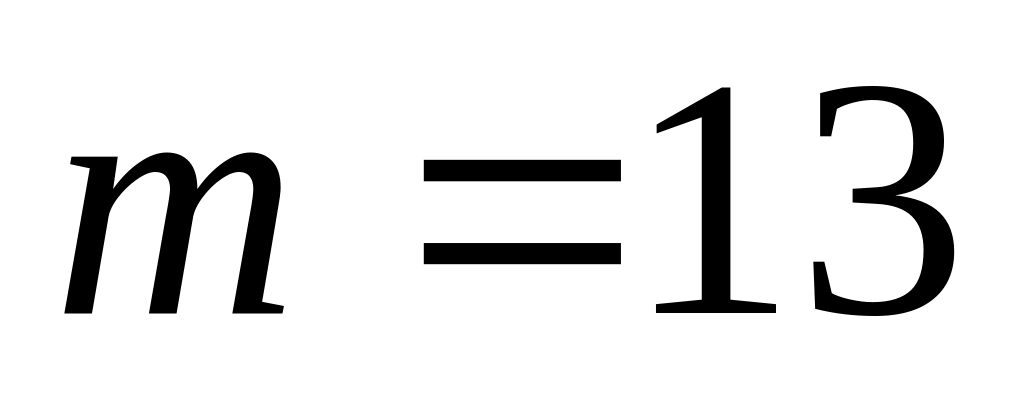 .
.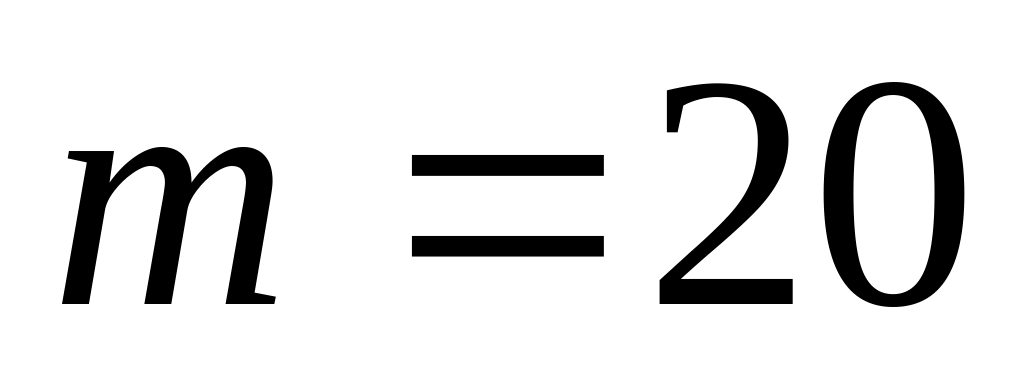 ,
,
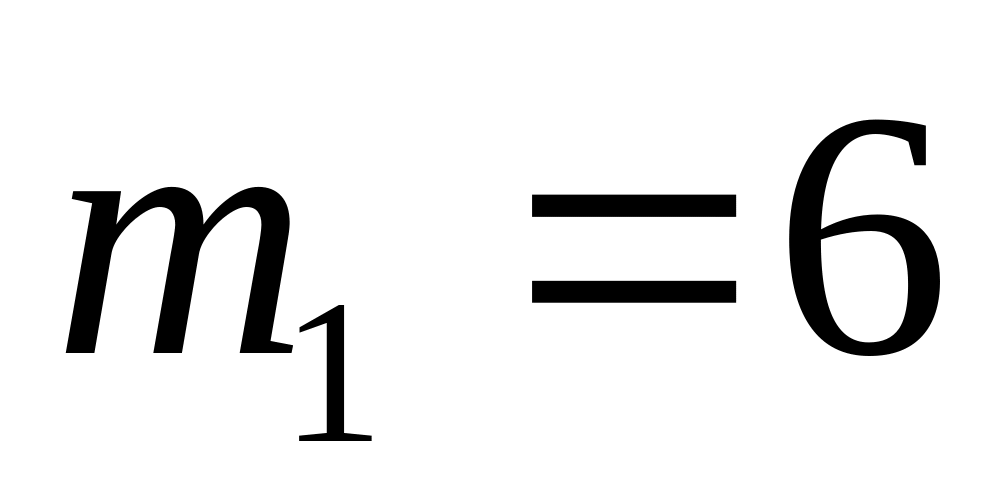 .
.; ; .
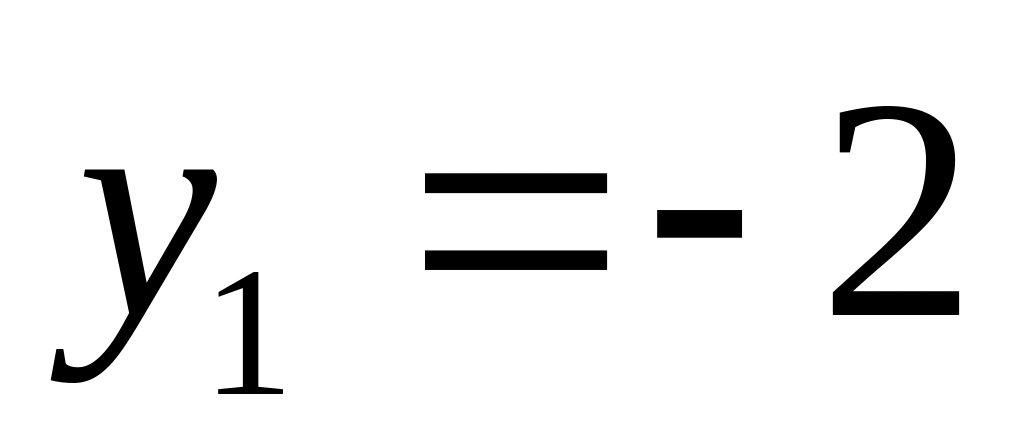 ;
;
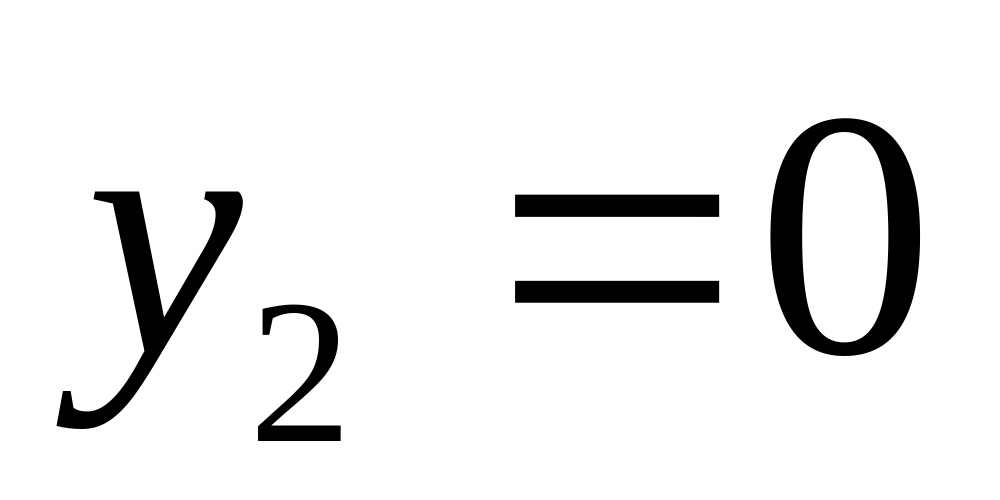 ;
;
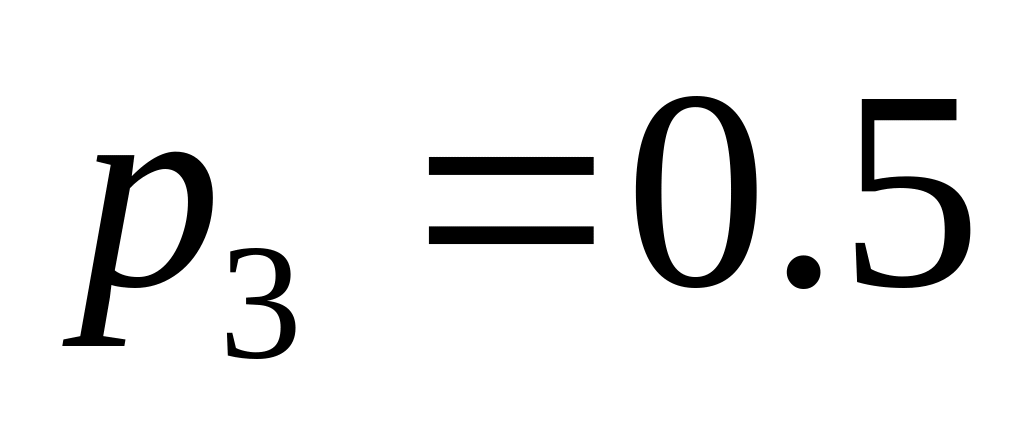 .
.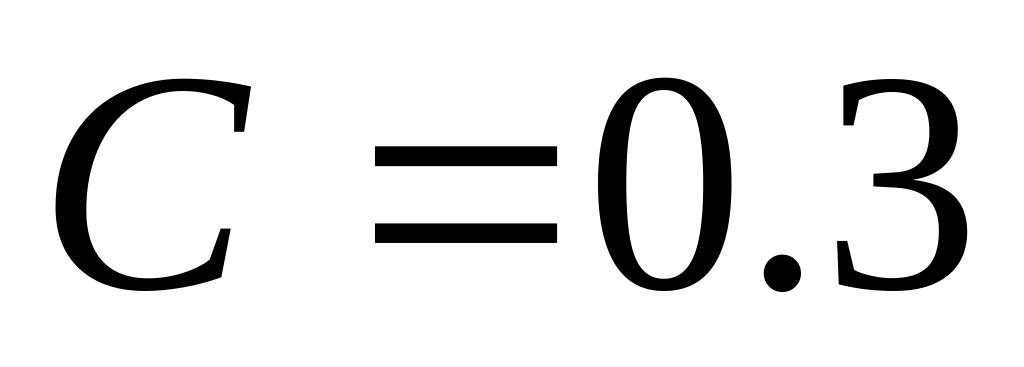 .
.
Вариант №9
задание 1 из варианта №1.
задание 2 из варианта №2.
задание 3 из варианта №3.
задание 4 из варианта №4.
задание 5 из варианта №5.
задание 6 из варианта №6.
задание 7 из варианта №7.
Пример данных к варианту №9
- {ровно одно сообщение передано верно}.
, .
; ; ;
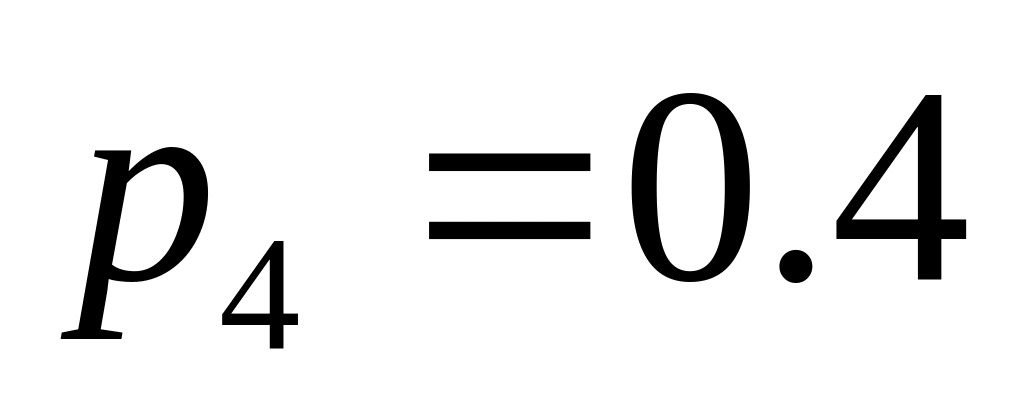 .
.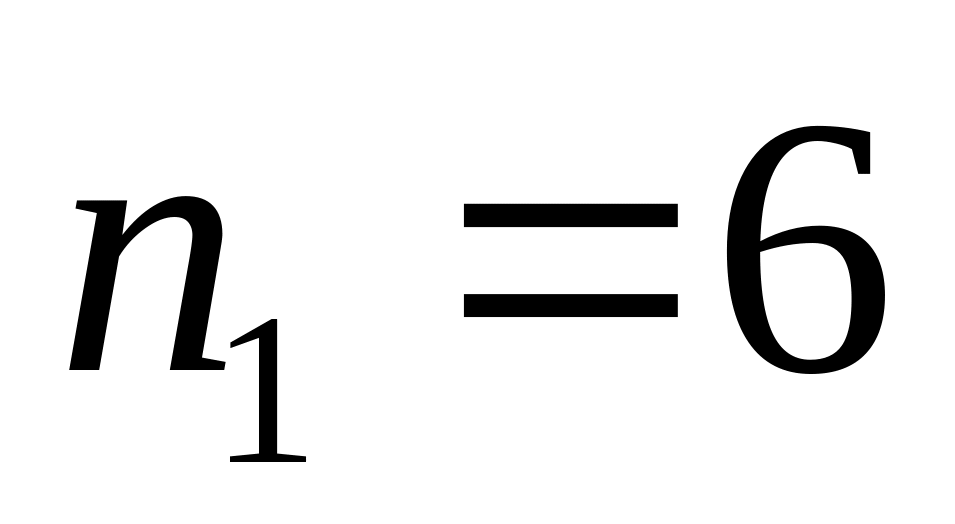 ;
;
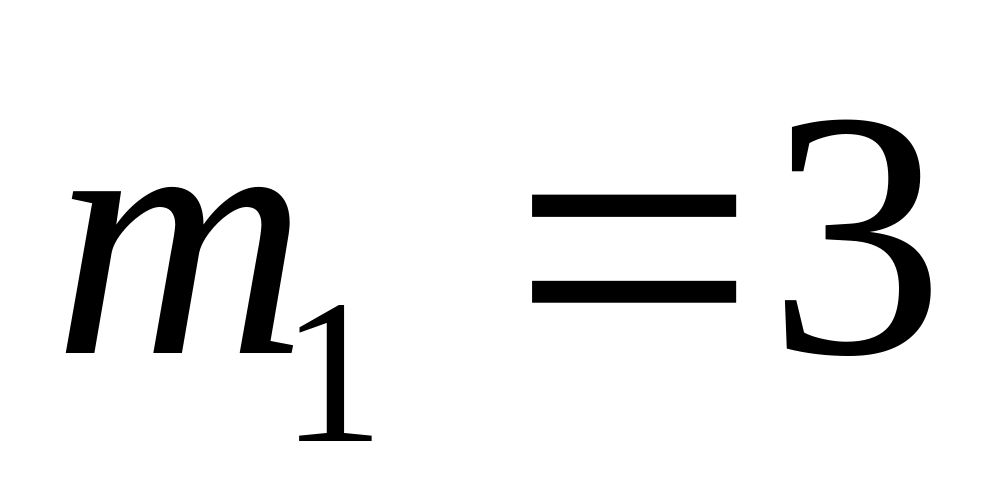 ;
;
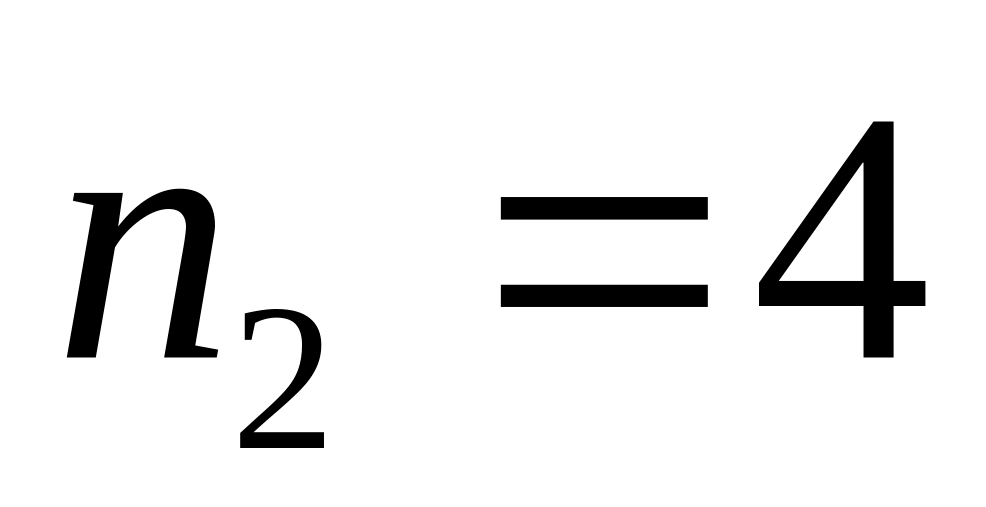 ,
,
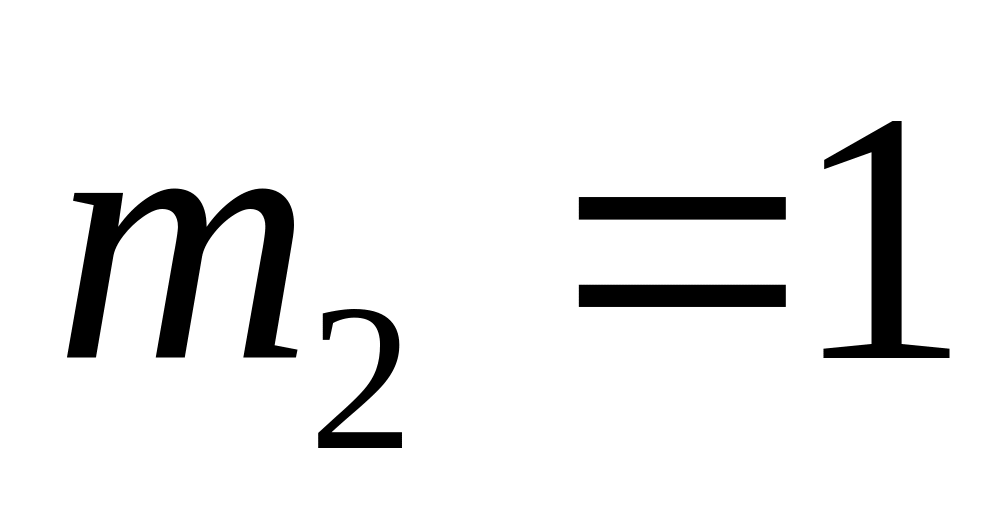 ,
,
,
,
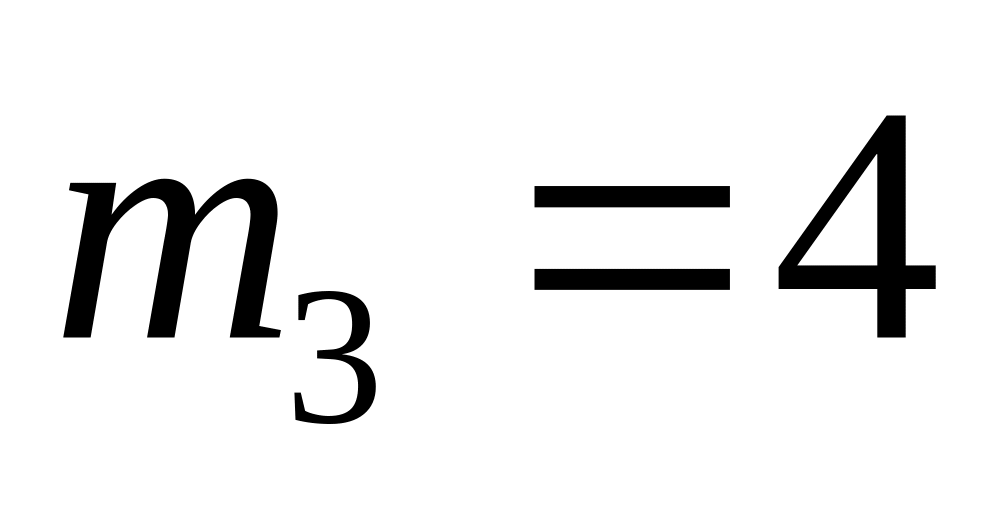 .
.;
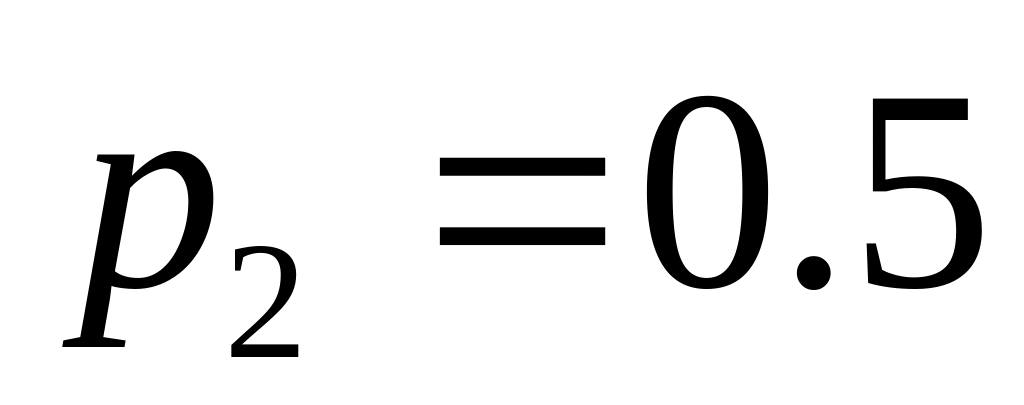 ;
;
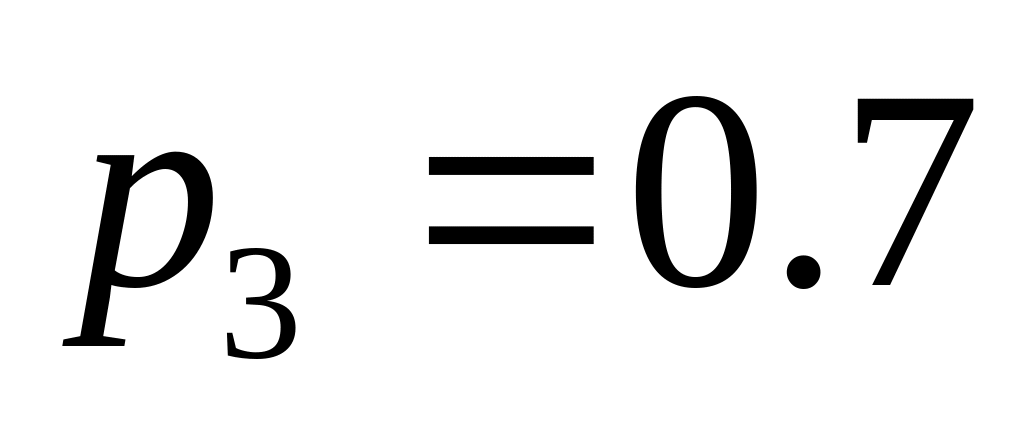 .
.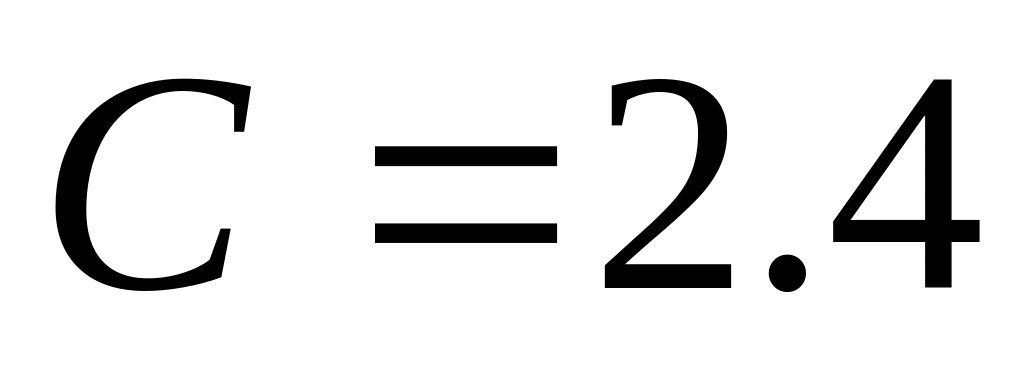 ;
;
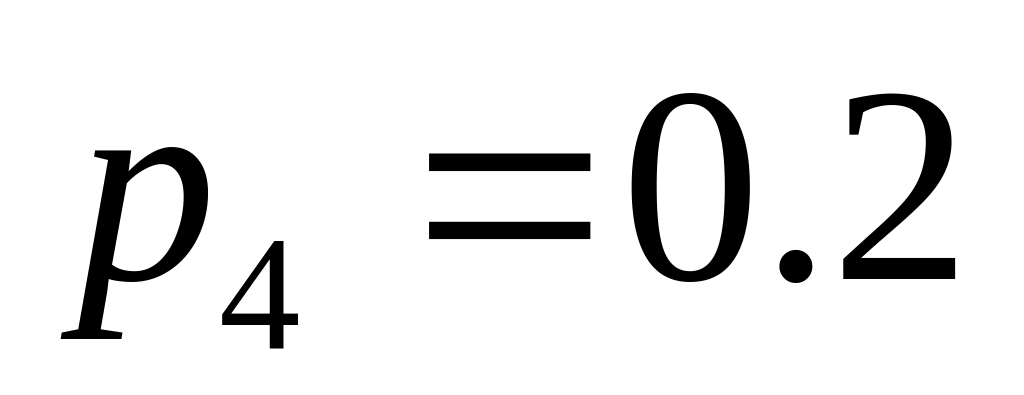 .
.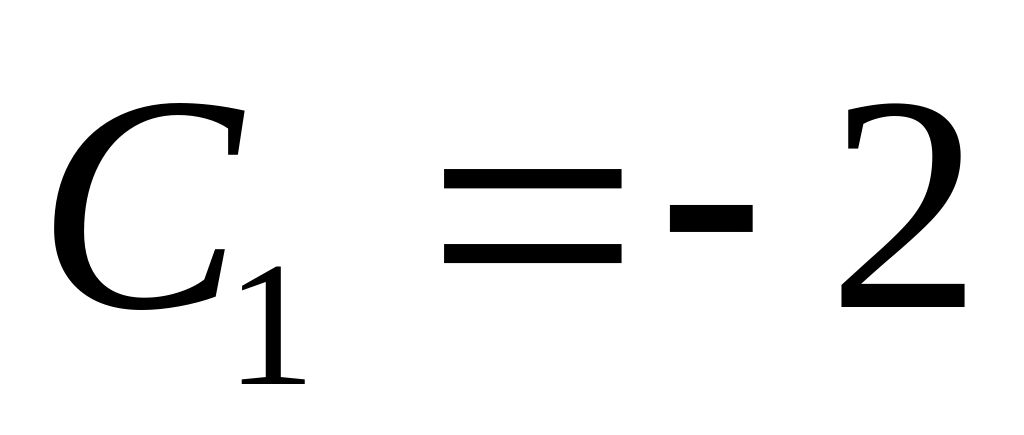 ,
.
,
.
Решение заданий варианта №9
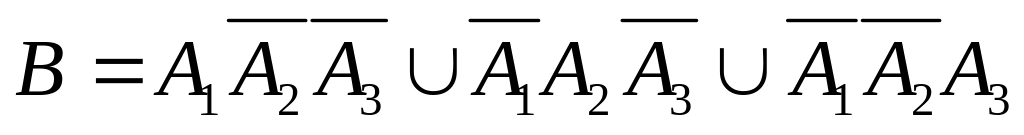 .
.Банки пронумеруем (от 1 до 10). Обозначим через
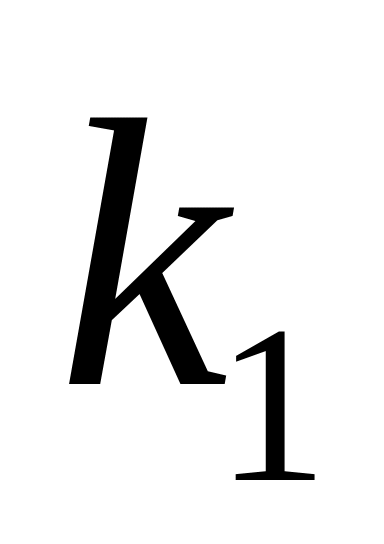 ,
,
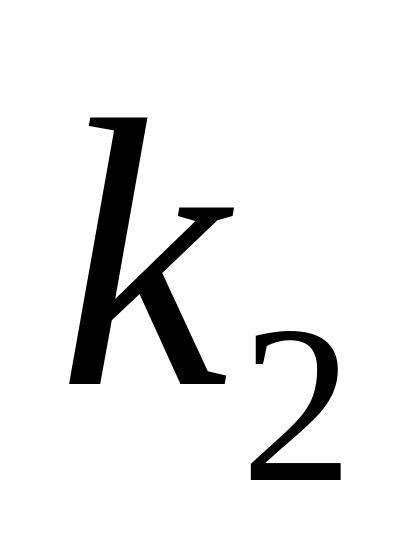 ,
,
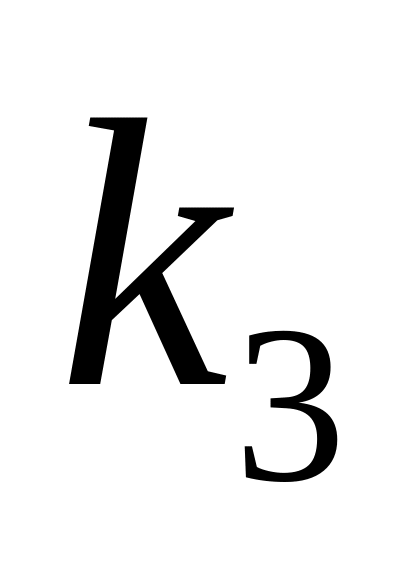 номера вскрытых банок. В качестве
элементарного исхода
номера вскрытых банок. В качестве
элементарного исхода
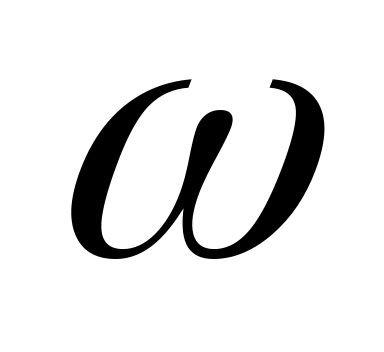 выберем неупорядоченный набор
выберем неупорядоченный набор
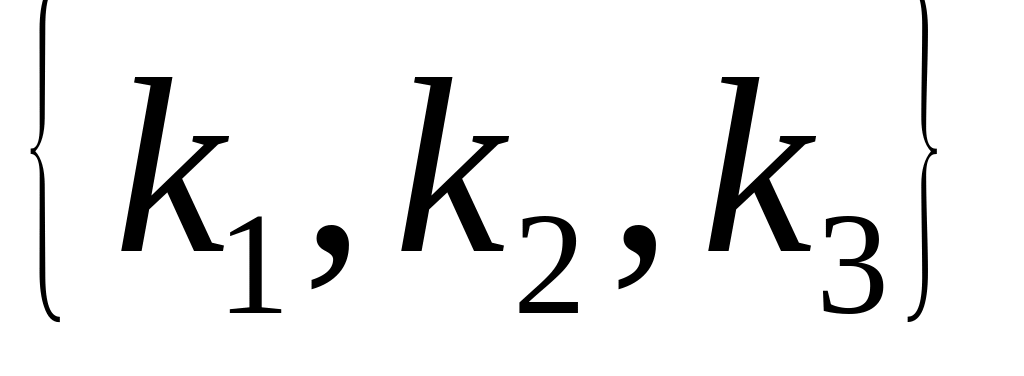 ,
в котором:
,
в котором:
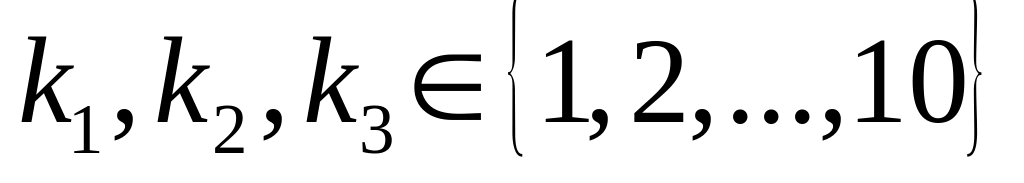 и все элементы различны. Для нахождения
применим формулу классического
определения вероятности:
и все элементы различны. Для нахождения
применим формулу классического
определения вероятности:
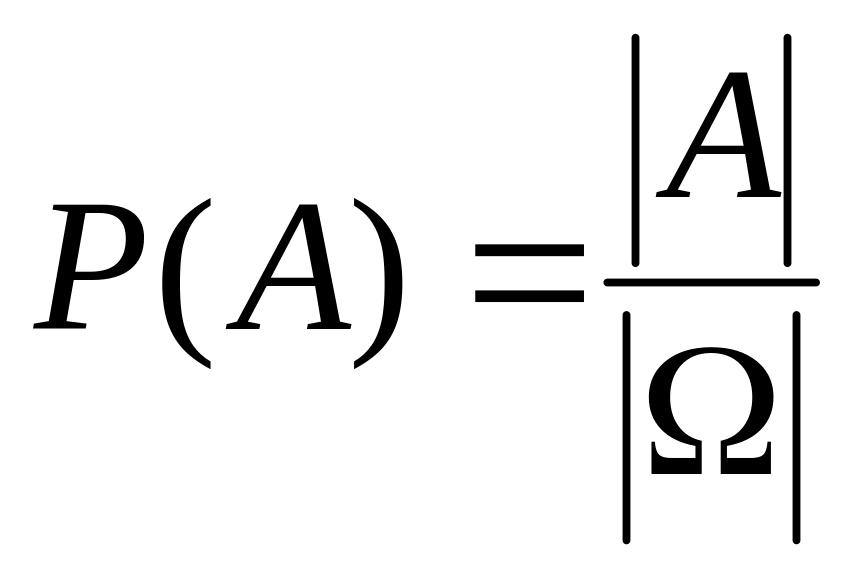 .
Здесь
.
Здесь
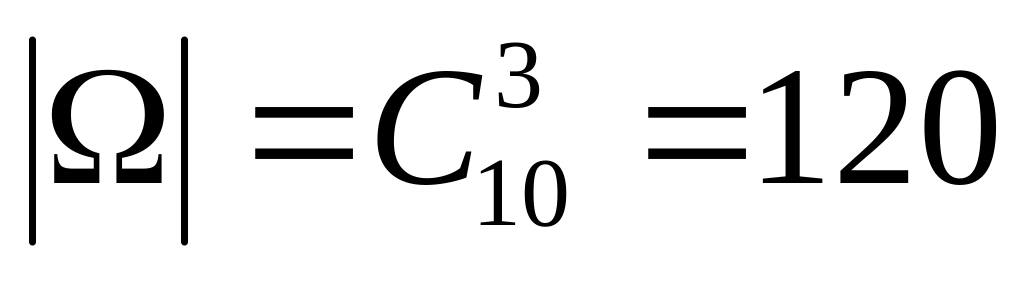 ;
;
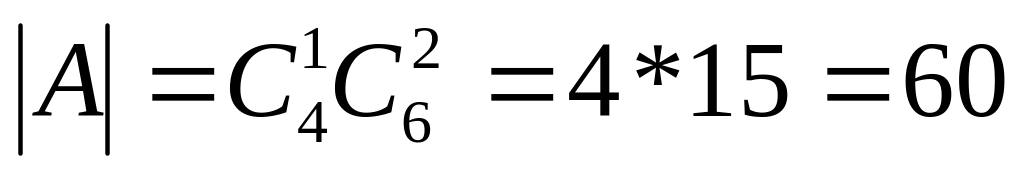 .
Следовательно
.
Следовательно
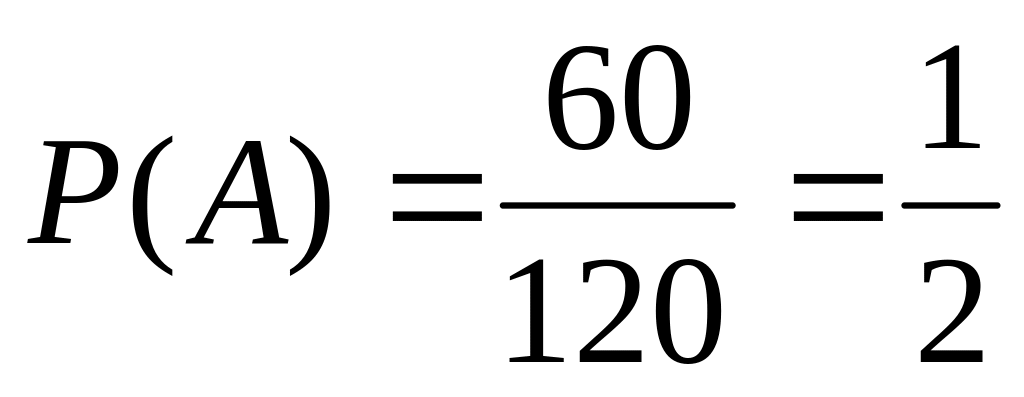 .
.Введем дополнительные события:
- {элемент вышел из строя},
![]() - {элемент
вышел из строя},
- {элемент
вышел из строя},
- {элемент вышел из строя},
- {элемент вышел из строя}.
Тогда
![]() .
.
Применяя теорему
сложения совместных событий и теорему
умножения независимых в совокупности
событий, получим:
![]()
![]() =0,1*0,2*0,2+0,4-0,1*0,2*0,2*0,4=0,4024.
=0,1*0,2*0,2+0,4-0,1*0,2*0,2*0,4=0,4024.
Введем гипотезы:
![]() - {выбран
первый альбом},
- {выбран
первый альбом},
![]() - {выбран второй
альбом},
- {выбран второй
альбом},
![]() - {выбран третий
альбом}.
- {выбран третий
альбом}.
![]() .
.
- {взятая фотография оказалась цветной}.
Найдем
![]() по формуле Байеса:
по формуле Байеса:
![]() .
.
Здесь
![]() ;
;
![]() ;
;
![]() .
.
Следовательно,
![]()
С.в. имеет значения: 0, 1, 2, 3.
Для нахождения вероятностей в ряде распределения введем события:
- {первый прибор вышел из строя},
- {второй прибор вышел из строя},
- {третий прибор вышел из строя}.
Тогда, используя теорему сложения попарно несовместных событий и теорему умножения независимых в совокупности событий, получим:
![]() .
.
![]()
![]()
![]() .
.
Искомый ряд распределений будет иметь вид:
-
0
1
2
3
0,105
0,395
0,395
0,105
Проверка:
![]() .
.
Найдем из условия нормировки:
![]() .
.
![]() .
.
Отсюда получим:
![]() ,
,
![]() .
.
С учетом условия:
![]() найдем
найдем
![]() .
.
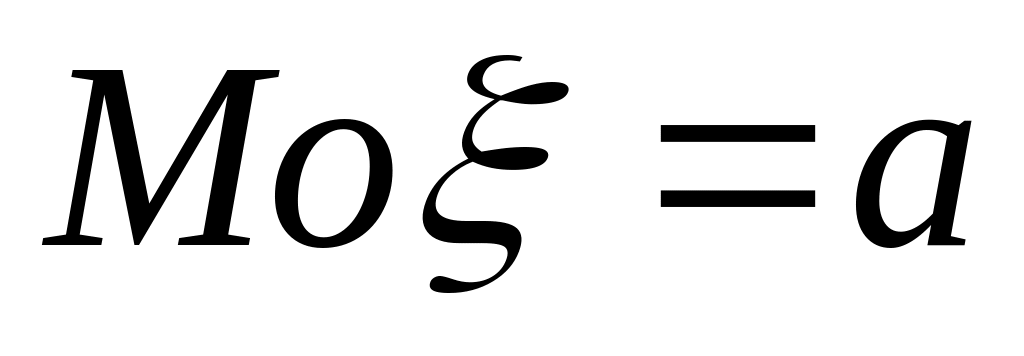 .
Следовательно,
.
Следовательно,
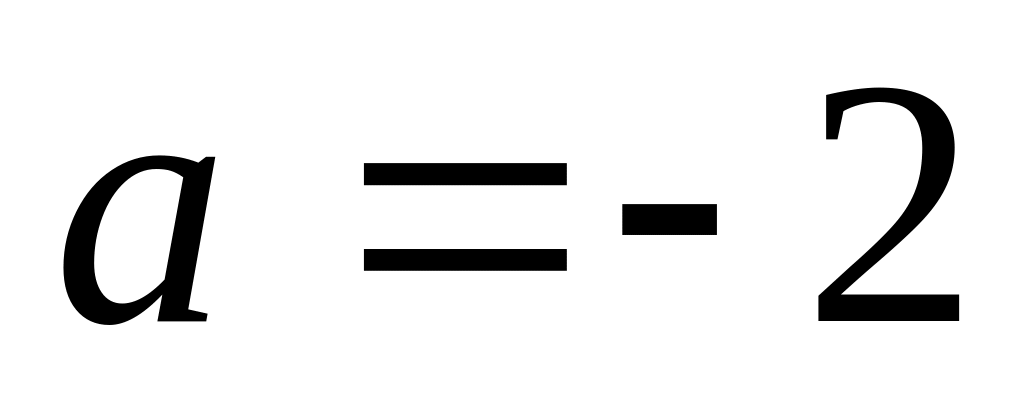 .
.
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Тогда
![]() .
.
