1.1. Аппроксимация функции с помощью ряда Фурье
Разложение функции в ряд Фурье означает её приближённую замену тригонометрическим полиномом вида
где T = 2π/ω1 = 2π/10 = 0,6283 с – время полного оборота кривошипа,
-
амплитуда сигнала на j-ой
частоте.
Частота сигнала для j-й гармоники θj =2πj/T.
Поскольку в данном случае функция F(t) задана таблицей значений в конечном числе точек m, то максимальное число членов ряда nmax = m/2.
Формулы для вычисления коэффициентов ряда Фурье при табличном задании функции:
,
где Fi - значения функции F(ti), i = 0, 1, 2, … m-1.
На первом этапе F(t) разложим в ряд с максимально возможным числом членов: n = 18 = n max = m/2 = 18 (рис. 3). В этом случае значения ряда Фурье в узлах практически совпадают с данными эксперимента.
Результаты дифференцирования ряда по времени представлены на рис. 4. На графике скорости и особенно ускорения явно видны паразитные осцилляции, вызванные погрешностями замера значений. Возникает необходимость сглаживания этих зависимостей.
Рис.3
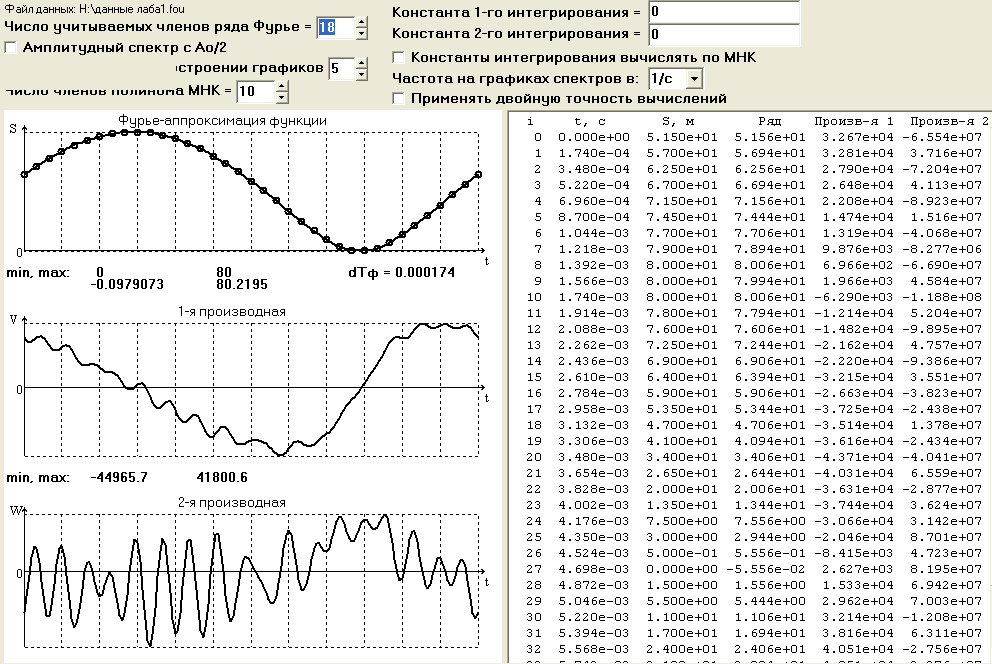
Рис.4
Анализ амплитудного спектра исследуемой функции (рис. 5) показывает, что существенным, кроме А0/2, являются лишь слагаемые ряда, соответствующие 1-й, 2-й и 3-й частотам, поэтому проведём разложение в ряд и аппроксимацию функции с учётом только этих частот.
i Част.,1/c Част., гц Ci Фазы i
0 0.000e+00 0.000e+00 4.494e+01
1 1.003e+03 1.596e+02 3.899e+01 0.0535
2 2.006e+03 3.193e+02 4.583e+00 -1.4710
3 3.009e+03 4.789e+02 1.149e+00 0.0628
4 4.012e+03 6.386e+02 2.878e-01 -1.1380
5 5.015e+03 7.982e+02 6.001e-02 -0.0027
6 6.018e+03 9.579e+02 7.349e-02 -1.2373
7 7.021e+03 1.117e+03 5.919e-02 -0.4158
8 8.025e+03 1.277e+03 3.956e-02 -1.5264
9 9.028e+03 1.437e+03 5.556e-02 0.0000
10 1.003e+04 1.596e+03 4.139e-02 0.0807
11 1.103e+04 1.756e+03 1.133e-01 1.2851
12 1.204e+04 1.916e+03 7.349e-02 1.2373
13 1.304e+04 2.075e+03 3.362e-02 -0.3619
14 1.404e+04 2.235e+03 1.019e-01 0.6740
15 1.505e+04 2.395e+03 7.260e-02 1.4617
16 1.605e+04 2.554e+03 3.578e-02 -0.9120
17 1.705e+04 2.714e+03 7.172e-02 -0.2641
18 1.806e+04 2.874e+03 1.111e-01 1.5708
Рис.5
Рис.6
Рис.7
На рис. 6 и 7 представлены результаты аппроксимации при учете первых 3-х членов ряда. Их анализ показывает, что функция аппроксимирована удовлетворительно, она сохраняет периодичность, графики 1-й и 2-й производных не зашумлены.
1.2. Аппроксимация функции с помощью полиномов, коэффициенты которых определены методом наименьших квадратов.
Суть метода состоит в том, что в случае необходимости сглаживания функции, её заменяют на другую, более гладкую, график которой проходил как бы проходил «между» точками исходной функции и был более гладким.
По методу МНК функцию строят в виде суммы простых аналитических функций , выбор которых является отдельной задачей. В данном случае используется система степенных функций 1,t,t2,t3,…Так что нужная гладкая функция получается в виде полинома: a0+a1t+a2t2+a3t3…+antn , где n- задаваемое пользователем число членов полинома.
Таким образом, задача сводится к нахождению коэффициентов аi таких, чтобы график полинома проходил между точками исходной функции, минимизируя среднее квадратическое отклонение.
Опытным путём выберем число полиномов МНК=6(во всех остальных график функции зашумлён).
Проведём аппроксимацию:
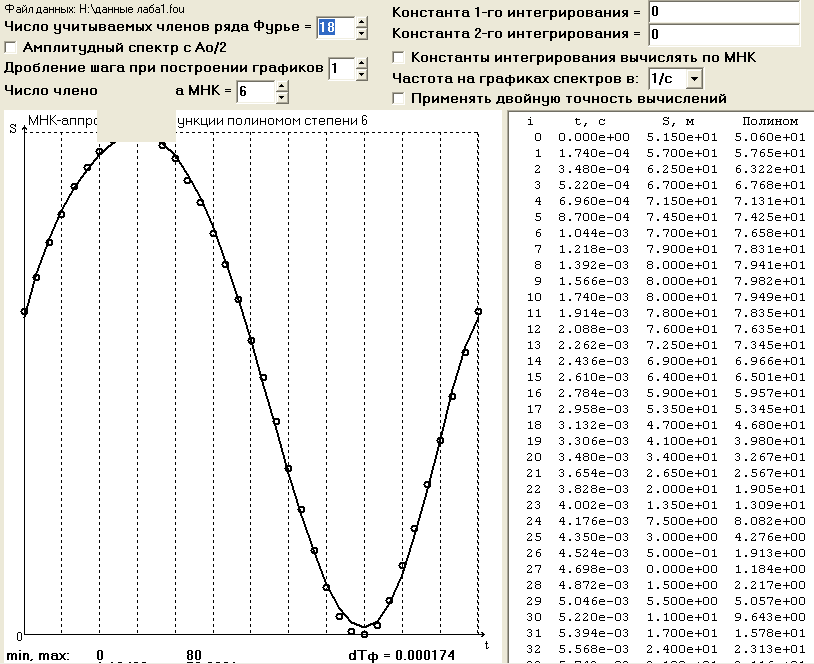
Рис.8
Рис.9
Рис.9
При n=6 функция аппроксимирована удовлетворительно, за исключением экстремумов (рис.8). Графики 1-й и 2-й производных не зашумлены, однако не соблюдена периодичность на краях производных.
Выбираем число членов полиномов МНК=6, в данном случае можно сказать, что функция аппроксимирована удовлетворительно, за исключением экстремумов ( здесь график аппроксимирующей функции проходит неточно).