
- •Уд.2. Обработка простых документов. Операции над таблицами
- •13. (Химанализ.)
- •Уш.З. Иерархия типов данных
- •15. (К годовому отчету.) в каждой компоненте файла ста-тистика-по-рапо содержатся следующие сведения:
- •16. (Обработка файла платежи,- Формирование новых файлов.) в каждой компоненте файла платежи содержатся следующие сведения:
- •17. (Итоги экзаменационной сессии.) Каждая компонента файла сессия содержит следующие данные из экзаменационной ведомости:
- •18. (Контроль ключевого поля.) в каждой компоненте файла кадры содержится:
- •19. (Обработка файла поставки. - Упорядоченные файлы.) Каждая компонента файла поставки содержит:
- •20. (Поквартальный план.) Каждая компонента исходного файла поквартальный-план, имеющего отношение к выпуску обуви некоторым предприятием, содержит:
- •21. (Подписная компания.) Каждая компонента файла подписные издания содержит:
- •1.2. При составлении одношаговых заданий рекомендуется рассмотреть следующие виды наборов данных:
Составители В.С.Кугураков, Р.К.Самитов
Настоящая работа предназначена для студентов, изучающих программирование на современных ЭВМ, а также для преподавателей, ведущих практические занятия по программированию. Учебный материал представлен задачами для программирования, которые рекомендуется использовать при изучении следующих тем: ЗАПИСИ, ФАЙЛЫ, ЯЗЫК управления ЗАДАНИЕМ.
Только философы имеют дело с реальным миром.
И.Флорес, Структуры и управление данными [7] . Проектировщик вычислительной системы пытается ь реальный мир путем структуризации данных. И.Флорес, там же.
УШ. ЗАПИСИ
ЗАПИСИ (record 'ы - в Паскале и Аде, struct ^ ы - в Алголе-68), как и МАССИВЫ, - это составные объекты, т.е. совокупности компонент. Принципиальное различие между массивами и записями обусловлено различиями в правилах построения этих объектов и способах идентификации компонент:
Массив - это регулярная (однородная) структура: все компоненты (элементы) массива должны быть одного типа. Доступ к тому или иному элементу массива осуществляется путем указания индекса (номера) соответствующего элемента (заметим, что в определении массива устанавливается некоторая нумерация его элементов) .
Запись - это комбинированная структура: компоненты (поля) записи могут быть неоднородными, т.е. различных типов. Доступ к тому или иному полю записи осуществляется путам указания имени соответствующего поля (в определении записи все ее поля должны быть снабжены явными именами).
Общее свойство массивов и записей заключается в том, что это - структуры с произвольным доступом: возможен непосредственный (прямой) доступ к любой компоненте. Запись - более универсальная структура по сравнению с массивом, поскольку ее компоненты могут иметь разные типы. С другой стороны, массив -более гибкая и динамичная структура: переход от одного элемента массива к другому (например, в цикле) может быть легко осуществлен путем изменения вычисляемого индекса, тогда как структура записи таких возможностей не предоставляет: имена полей - это фиксированные (постоянные) идентификаторы, а не вычисляемые значения.
Массивы и записи можно комбинировать, получая целую иерархию структур типа "массив записей", "запись с компонентами-массивами" и пр., а также использовать для моделирования таких динамических информационных структур, как стеки, очереди, линейные связанные списки, деревья и пр. Отметим также, что компонентами файлов обычно являются записи.
УШ.1. Использование ЗАПИСЕЙ для представления простейших математических объектов
1. (Возврат.) Вернуться к задачам 4-11 (о треугольнике на плоскости) и 57-60 (о комплексных числах) из [б ] .
Мотивация: использование записей для представления таких объектов, как точки на плоскости и комплексные числа.
2. (Алгебра квартенионов.) Кватернион q может быть
представлен в виде
(*
)
![]()
где
![]() -
действительные (вещественные) числа,
I
- обычная
единица, а
-
действительные (вещественные) числа,
I
- обычная
единица, а
![]() -
специальные
кватернионы (т.н. ква-тернионные единицы),
подчиняющиеся следующим правилам
умножения:
-
специальные
кватернионы (т.н. ква-тернионные единицы),
подчиняющиеся следующим правилам
умножения:
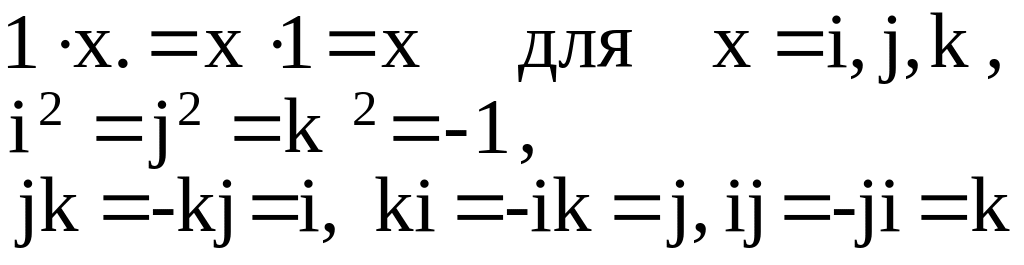
Операции
над кватернионами выполняются естественным
образом (но, конечно, с учетом соотношений
для единиц
I,
i,j,k
).
Например,
если
![]() и
и![]() ,
,
тo
![]() называется
сопряженным к кватерниону
называется
сопряженным к кватерниону![]() .
.
Кватернион![]() .
Действительное число
.
Действительное число![]() называется
нормой кватерниона
. Отметим, что
называется
нормой кватерниона
. Отметим, что ![]() .
?
.
?
Оформить в виде подпрограмм основные операции над кватернионами : вычисление
а)
![]() -
сопряженного к
-
сопряженного к
![]() кватерниона;
кватерниона;
б)
![]() +
+![]() -
суммы кватернионов
и
;
-
суммы кватернионов
и
;
в)
![]() -
произведения кватернионов
и
(заметим, что произведение не коммутативно);
-
произведения кватернионов
и
(заметим, что произведение не коммутативно);
г)
![]() -
нормы кватерниона
;
-
нормы кватерниона
;
д)
![]() -
обратного к кватерниону
.
-
обратного к кватерниону
.
Замечание. Кватернионы, введенные У.Гамильтоном в 1843 году, тесно связаны с векторным исчислением, и исторически последнее возникло из кватернионов. Интересно отметить (хотя это и не относится к существу нашей задачи), что множество H кватернионов является единственным расширением поля С комплексных чисел, которое образует некоммутативную алгебру с делением над полем R действительных чисел. Согласно теореме Фробениуса над полем R существуют лишь три конечномерные ассоциативные алгебры с делением: R, С и Н .
3.
(Аналитическая геометрия в пространстве.)
Точки трехмерного евклидова пространства
задаются радиус-векторами
![]() ,
которые
в декартовой системе координат
представлены тройками
,
которые
в декартовой системе координат
представлены тройками
![]() вещественных
чисел.
вещественных
чисел.
а) Реализовать следующие операции над Векторами, оформляя их в виде подпрограмм:
1)
вычисление модуля
![]() вектора
;
вектора
;
2)
умножение вектора
на скаляр
![]() ;
;
3)
сложение векторов
и
![]() ;
;
4)
вычисление скалярного произведения
(
![]() )
векторов
и
;
)
векторов
и
;
5)
вычисление векторного произведения
![]() векторов
и
.
векторов
и
.
Напомним необходимые формулы:
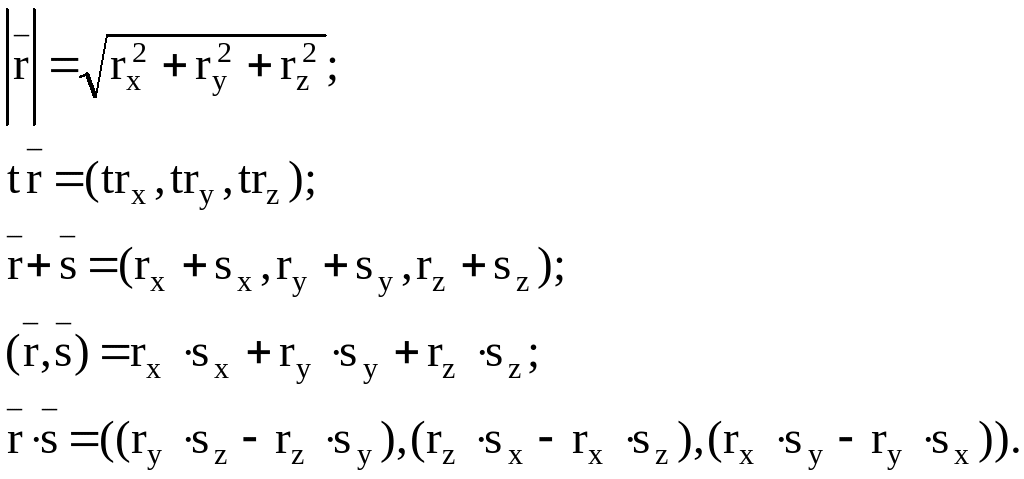
- 5 -
б) Вычислить:
1)
S
—
площадь параллелограмма, построенного
на векторах
![]() и
и
![]()
![]()
2)
V
-
объем параллелепипеда, построенного
на векторах
,
и
![]()
![]()
3)
![]() -
объем тетраэдра, вершины которого заданы
векторами
-
объем тетраэдра, вершины которого заданы
векторами
![]()
![]()
в)
Установить, лежат ли три точки
![]() , заданные
радиус-векторами
, заданные
радиус-векторами![]() ,
на одной прямой. (Ответ положителен
тогда и только тогда, когда
,
на одной прямой. (Ответ положителен
тогда и только тогда, когда
![]()
г)
Установить, лежат ли четыре, точки
![]() ,
заданные
радиус-векторами
,
заданные
радиус-векторами
![]() ,
в одной плоскости. (Ответ положителен
тогда и только тогда, когда
,
в одной плоскости. (Ответ положителен
тогда и только тогда, когда
![]()
д)
Плоскость задана параметрическим
уравнением
![]() (
(
![]() -
радиус-вектор
произвольной точки плоскости;
-
радиус-вектор
произвольной точки плоскости;
для
задания плоскости достаточно задать
векторы
,
![]() и
и
![]() ). Вычислить
расстояние ?
). Вычислить
расстояние ?![]() от точки
от точки
![]() ,
заданной радиус-вектором
,
заданной радиус-вектором
![]() ,
до плоскости по формуле
,
до плоскости по формуле
![]()
е)
Положение точки
![]() в трехмерном пространстве может быть
задано не только декартовыми координатами
(x,y,z),
но
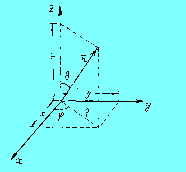
и другими способами. На рис.1, наряду с
декартовыми координатами, показаны
также цилиндрические координаты
(,,z)
и сферические координаты
(r,,
)
=
(полярный радиус, широта, долгота).
в трехмерном пространстве может быть
задано не только декартовыми координатами
(x,y,z),
но
и другими способами. На рис.1, наряду с
декартовыми координатами, показаны
также цилиндрические координаты
(,,z)
и сферические координаты
(r,,
)
=
(полярный радиус, широта, долгота).
1)
Для точки
![]() ,
заданной декартовыми координатами,
вычислить ее цилиндрические и сферические
координаты.
,
заданной декартовыми координатами,
вычислить ее цилиндрические и сферические
координаты.
2) Выполнить обратное преобразование: переход от цилиндрических и сферических координат к декартовым.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. I. Системы координат: декартова (x,y,z), цилиндрическая (,,z) и сферическая (r,,).
ж) Для городов А и Б (на поверхности геоида, т.е. земного шара) известны их координаты - широта и долгота. Вычислить расстояние d между городами.
Указание.
Для векторов
![]() и
и
![]() ,
задающих точки А и Б, перейти от сферических
координат к декартовым. После этого
можно вычислить (в радианах ) угол
между
векторами, учитывая, что
,
задающих точки А и Б, перейти от сферических
координат к декартовым. После этого
можно вычислить (в радианах ) угол
между
векторами, учитывая, что
![]() .
Но
тогда
.
Но
тогда
![]() где
R-
радиус
земного шара. Это
-
идея. Потребуется, однако,
заглянуть
в учебник географии, чтобы уточнить,
как задаются координаты точек на земной
поверхности. В рекомендуемом подходе
к решению задачи, конечно, присутствует
элемент абстрагирования от реальной
действительности: земной шар не является
ни правильным шаром, ни даже эллипсоидом.
где
R-
радиус
земного шара. Это
-
идея. Потребуется, однако,
заглянуть
в учебник географии, чтобы уточнить,
как задаются координаты точек на земной
поверхности. В рекомендуемом подходе
к решению задачи, конечно, присутствует
элемент абстрагирования от реальной
действительности: земной шар не является
ни правильным шаром, ни даже эллипсоидом.
4.
(Рациональные числа.) Всякое рациональное
число есть дробь
![]() ,
где p
,q
-
целые числа, q
>0
,
и может быть представлено парой
(p
,q
).
,
где p
,q
-
целые числа, q
>0
,
и может быть представлено парой
(p
,q
).
Оформить в виде подпрограмм основные операции над рациональными числами (арифметика, приведение к несократимым).
Мотивация: точные вычисления.
5. (Многочлены. - Возврат к задачам 62 и 65 из [б] .) 'Оформить в виде подпрограмм основные операции над многочленами с вещественными коэффициентами.
Указание. Всякий многочлен может быть представлен парой ( n,a ), где n - степень многочлена, а a - массив, используемый для размещения коэффициентов многочлена. Длина массива a выбирается с некоторым запасом, поскольку степень многочлена может увеличиваться. Так, при перемножении многочленов степеней k и L получается многочлен степени k+L .
Уд.2. Обработка простых документов. Операции над таблицами
Рисунки, приводимые в данном и следующем подразделах, поясняют структуру документов - записей, которые необходимо
обработать.
6. (Описание структуры.) Описать переменную для данных
следующей структуры:
КУРС |
СПЕЦИАЛЬНОСТЬ
|
ЗАЧЕТЫ (не более семи названий предметов) |
ЭКЗАМЕНЫ (не более четырех названий предметов)
|
7. (Требование на книгу.) Бланк требования на книгу в библиотеке и карточка книжного каталога изображены на рис.2.
а) Используя карточку каталога, заполнить требование на книгу, указав конкретные сведения о читателе и дату
заказа.
б) Требование на книгу дополнить графой "куда", значением которой может быть "абонемент" или "читальный зал". Задание предыдущего пункта (заполнение требования) необходимо теперь выполнить лишь в том случае, если год издания книги >= 1886 или же книга запрашивается в читальный зал, (Чтобы сохранить уникальный книжный фонд, книги с годом издания < = 1885 на дом не выдают.) 6. (Телефонные разговоры.) Бланк извещения о телефонном разговоре изображен на рис.3. Используя заполненный бланк, вы-
СВЕДЕНИЯ О КНИГЕ СВЕДЕНИЯ О ЧИТАТЕЛЕ номер _____________ номер читательского автор_______________ билета____________________________ название___________ Фамилия__________________________
дата заказа_______________________
|
СВЕДЕНИЯ О КНИГЕ ВЫХОДНЫЕ ДАННЫЕ номер_________________ место издания________________ автор_________________ издательство__________________ название_____________ год издания____________________
|
Рис.2 ( к задаче 7). Бланк требования на книгу в библиотеке и карточка книжного каталога.
Номер телефона_____________ СВЕДЕНИЯ ОБ АБОНЕНТЕ СВЕДЕНИЯ О РАЗГОВОРЕ фамилия__________________ дата_______________________ адрес______________________ город______________________ номер счета_____________ время разговора_________ |
Рис.3 (к задаче 8). Бланк извещения о телефонном разговоре.
СВЕДЕНИЯ О ЖКО СВЕДЕНИЯ О ЖИЛЬЦЕ название организации_ адрес__________________ ___________________________ фамилия_______________ номер счета_____________ СВЕДЕНИЯ ОБ ОПЛАТЕ за какой месяц___________________________ год_______________ сумма___________________________________________________________ пени_____________________________________________________________ всего____________________________________________________________
|
Рис.4 (к задаче 9). Квитанция об оплате за коммунальные услуги.
Заполнить следующее задание:
Если номер телефона равен 999999, то сформировать значение переменной квитанция, содержащее:
- сведения об абоненте;
- стоимость разговора ( по 15 коп. за I мин.).
9. (Коммунальные услуги.) Квитанция об оплате за коммунальные услуги изображена на рис.4.
а) Ввести (например, с перфокарт) значения полей, кроме "пени" и "всего".
б) Вычислить значения полей "пени" и "всего". Способ подсчета: пени начисляется в размере 2% от указанной суммы, за каждый просроченный месяц (считая от текущей даты) .
10. (Продажа тканей.) 10 магазинов представили сведения о продаже ткани в метрах по следующей форме:
-
МАГАЗИН
ШЕРСТЬ
Х/Б
ЛЕН
СИНТЕТИКА
а) Подсчитать, сколько ткани каждого вида продано всеми, магазинами.
б) Подсчитать, сколько ткани заданного вида продано магазином с заданным названием.
11. (Составление отчета.)
а) Описать таблицу из 50 строк следующей структуры:
-
НАИМЕНОВАНИЕ ПРОДУКТА
ПЛАН
Выполнено
ПРОЦЕНТ
ВЫПОЛНЕНИЯ
б) Заполнить первые три графы таблицы, вводя данные с перфокарт.
в) Заполнить графу ПРОЦЕНТ ВЫПОЛНЕНИЯ.
г) Сформировать таблицу такой же структуры, но содержащую данные только о тех продуктах, по которым имеется невыполнение плана.
д) Напечатать таблицу.
е) Напечатать только данные из граф НАИМЕНОВАНИЕ ПРОДУКТА и ПРОЦЕНТ ВЫПОЛНЕНИЯ.
12. (Платежи.)
а) Описать таблицу из 100 строк следующей структуры:
ФАМИЛИЯ
1 |
НАЧИСЛЕНО 2 |
УДЕРЖАНО 3 |
УПЛАЧЕНО 4 |
ДОЛГ
5 |
б) Заполнить первую, вторую и пятую графы таблицы, вводя данные с перфокарт.
в) Заполнить третью и четвертую графы, изменяя при необходимости пятую графу. Придерживаться следующих правил расчета. Пусть m2,m3, m4,m5-значения соответствующих граф таблицы. Тогда, если m2>=m5), то положить m3=m5, m4=m2-m5, m5=0; если m2 m<m5 ,то положить m3 = m5 , m4=0 , m5=m5-m2.
г) Напечатать таблицу.
д) Напечатать только данные из граф ФАМИЛИЯ, УДЕРЖАНО, УПЛАЧЕНО.
е) Напечатать только те строки, для которых графа ДОЛГ имеет ненулевое значение.
