
Практическая работа 1: Множества и операции над ними
Краткие сведения из теории
Множество – это
совокупность предметов произвольной
природы, объединенных в единое целое
по какому – либо признаку, либо простым
перечислением предметов, входящих в
эту совокупность. Предметы, входящие в
такую совокупность, называются элементами
множества.
Запись:
![]() означает, что элемент
означает, что элемент
![]() принадлежит множеству (содержится во
множестве)
принадлежит множеству (содержится во
множестве)
![]() .
Запись:
.
Запись:
![]() означает, что элемент
не принадлежит множеству (не содержится
во множестве)
.
Утверждение, что множество
состоит из элементов
означает, что элемент
не принадлежит множеству (не содержится
во множестве)
.
Утверждение, что множество
состоит из элементов
![]() и только из них коротко записывается
так:
и только из них коротко записывается
так:
![]() .
.
Два множества
и
![]() называются равными, если они состоят
из одних и тех же элементов; в этом случае
пишут
называются равными, если они состоят
из одних и тех же элементов; в этом случае
пишут
![]() .
Например,
.
Например,
![]() ,
потому что оба множества состоят из
одних и тех же элементов. В то же время
,
потому что оба множества состоят из
одних и тех же элементов. В то же время
![]() ,
потому что элементом второго множества
является множество
,
потому что элементом второго множества
является множество
![]() ,
которого нет среди элементов первого
множества.
,
которого нет среди элементов первого
множества.
Если
множество не содержит ни одного элемента,
оно называется пустым и обозначается
символом
![]() .
Если же множество содержит все элементы,
которые, в принципе, можно использовать
при задач той или иной науки, то в данной
науке такое множество называют
универсальным и обозначают буквой
.
Если же множество содержит все элементы,
которые, в принципе, можно использовать
при задач той или иной науки, то в данной
науке такое множество называют
универсальным и обозначают буквой
![]() .
.
Для наглядного представления множеств используется их геометрическое изображение с помощью диаграмм Эйлера. Универсальное множество обычно изображается в виде квадрата. Любое другое множество изображается в виде некоторой фигуры внутри квадрата (см. рис. 1).
Множество
называется подмножеством множества
(иначе: множество
включается во множество
),
если любой элемент множества
принадлежит множеству
.
В таком случае пишут
![]() .
Включение множеств изображено на рис.2.
.
Включение множеств изображено на рис.2.
Множество
![]() называется дополнением множества
до универсального, если множество
называется дополнением множества
до универсального, если множество
![]() содержит только те элементы, которые
не принадлежат множеству
.
Множества
и
изображены на рис 3.
содержит только те элементы, которые
не принадлежат множеству
.
Множества
и
изображены на рис 3.
Над множествами можно проводить некоторые операции; рассмотрим основные из них. Пусть имеются множества и .
Объединением
множеств
и
называется новое множество
![]() ,
содержащее элементы или множества
,
или множества
,
или их общие элементы. Множество
изображено на рис 4.
,
содержащее элементы или множества
,
или множества
,
или их общие элементы. Множество
изображено на рис 4.
Пересечением множеств
и
называется новое множество
![]() ,
содержащее только общие элементы
множеств
и
.
Множество
изображено на рис 5. Множества, не имеющие
общих элементов, называются
непересекающимися. Ясно, что для
непересекающихся множеств
,
содержащее только общие элементы
множеств
и
.
Множество
изображено на рис 5. Множества, не имеющие
общих элементов, называются
непересекающимися. Ясно, что для
непересекающихся множеств
![]() .
.
Разностью множеств
и
называется новое множество
![]() ,
содержащее только те элементы множества
,
которые не содержатся во множестве
.
Множество
изображено на рис 6.
,
содержащее только те элементы множества
,
которые не содержатся во множестве
.
Множество
изображено на рис 6.

К онтрольные вопросы и упражнения
Какой объект называется множеством? элементом множества?
Что означает запись:
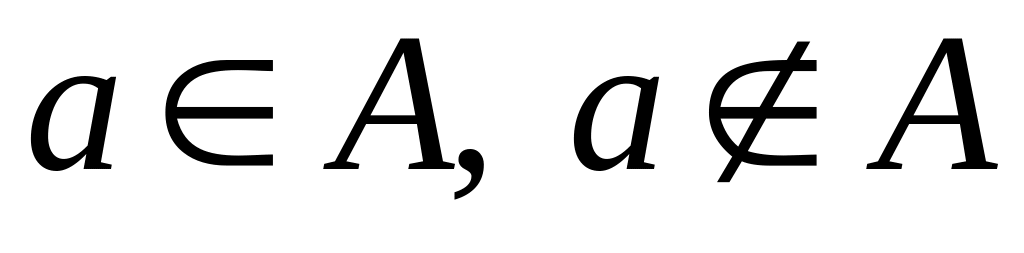 ?
?Какое множество называется пустым? универсальным?
Что понимается под диаграммами Эйлера?
Что означает запись ?
Дайте определение множеств:
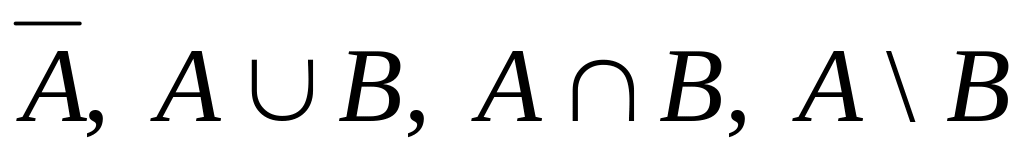 ?
Дайте геометрическое толкование этих
множеств.
?
Дайте геометрическое толкование этих
множеств.Какие множества называются непересекающимися?
С помощью диаграмм Эйлера докажите тождества: а)
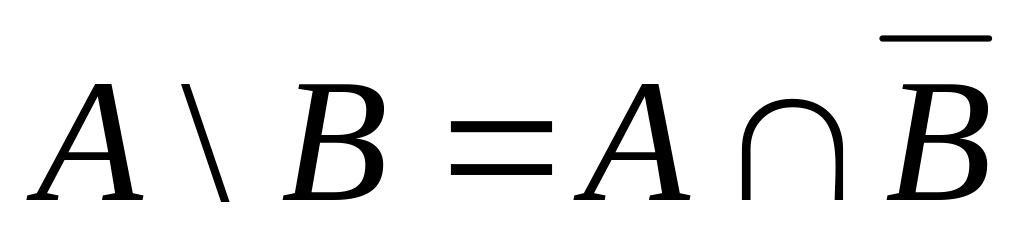 ;
б)
;
б)
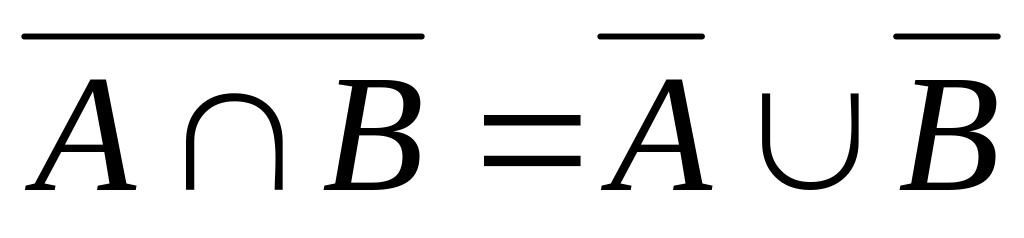 ;
в)
;
в)
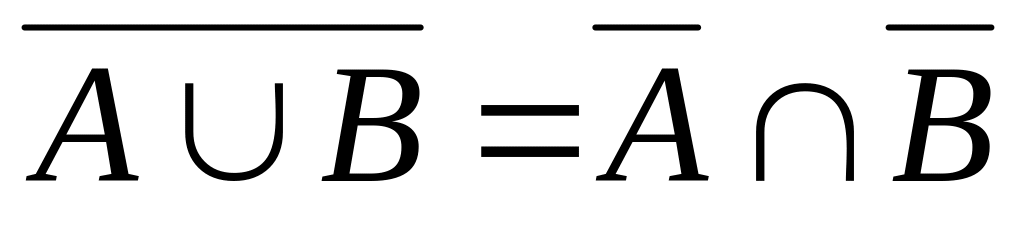 .
.Равны между собой множества и ? Если нет, то почему? а)
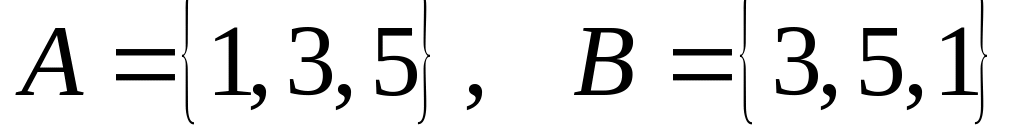 ;
б)
;
б)
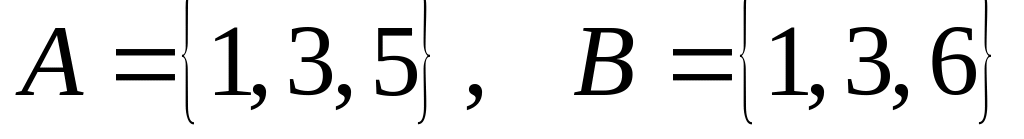 ;
в)
;
в)
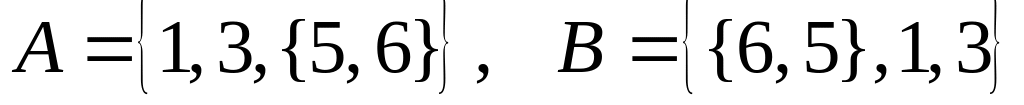 ;
г)
;
г)
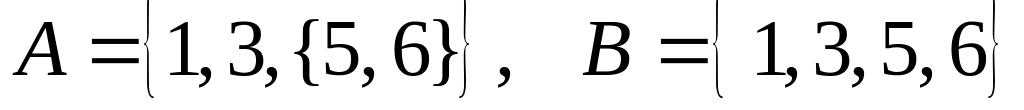 .
.Какие из утверждений верны / неверны и почему? а)
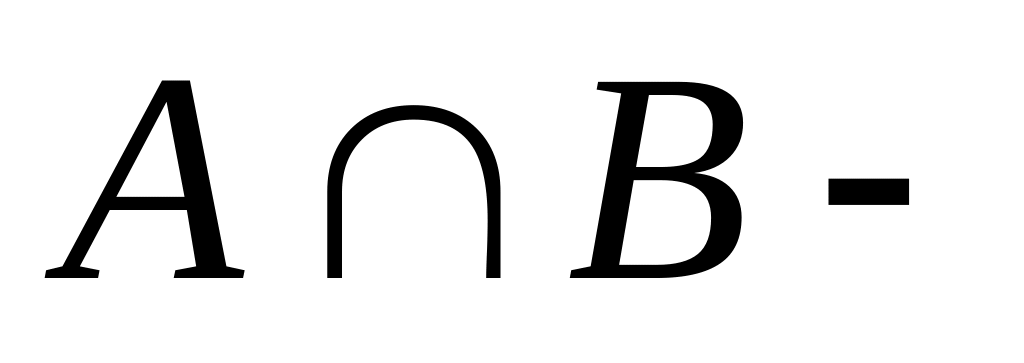 подмножество
;
б)
подмножество
;
б)
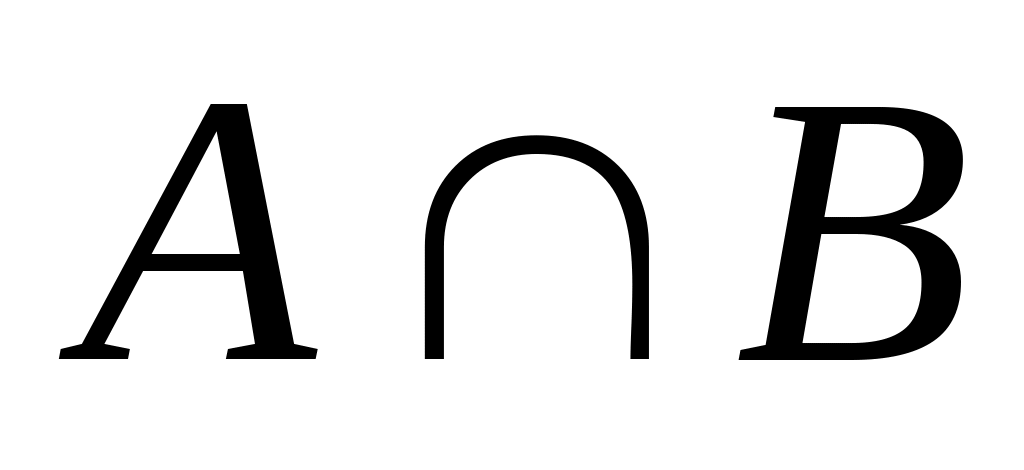 включается
в
;
в)
включается в
;
г)
включается
в
;
в)
включается в
;
г)
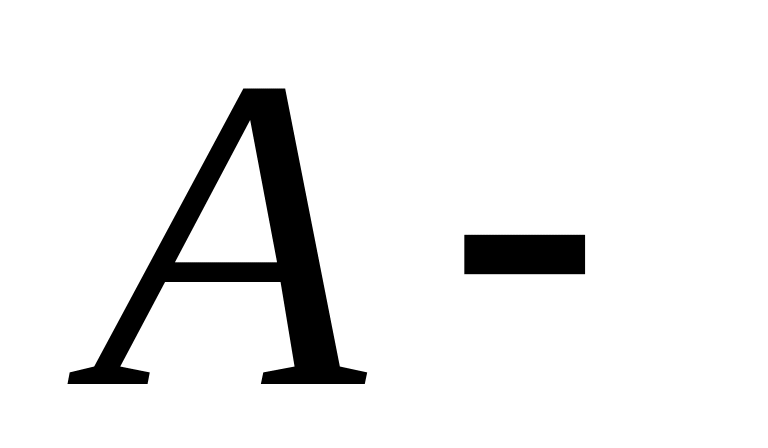 подмножество
подмножество
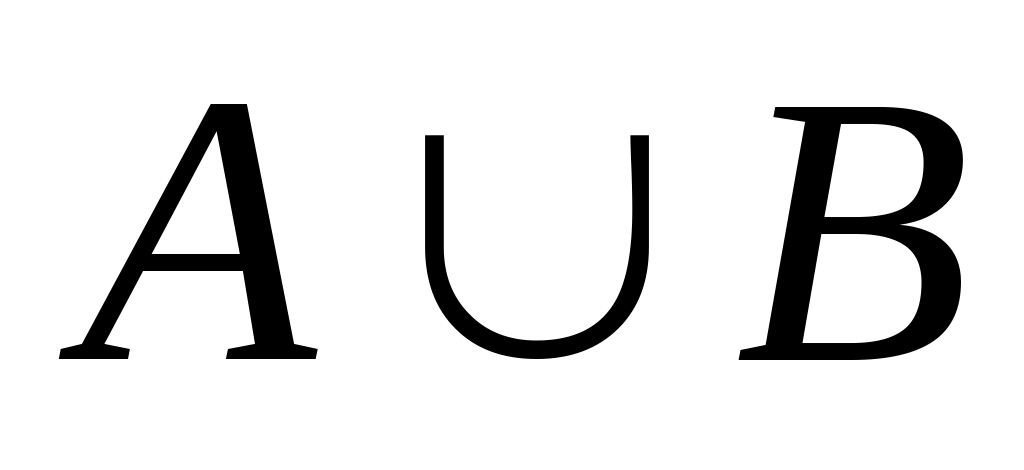 ;
д)
;
д)
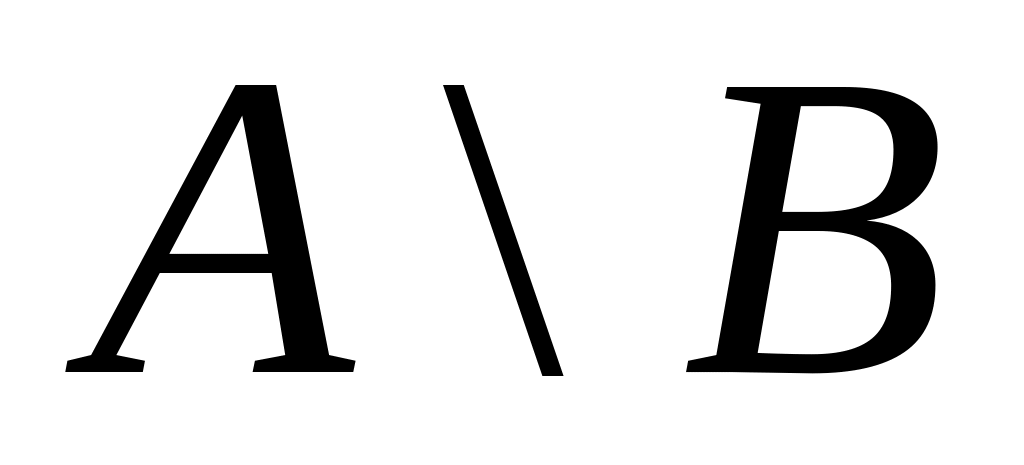 включается
в
;
е)
и
включается
в
;
е)
и
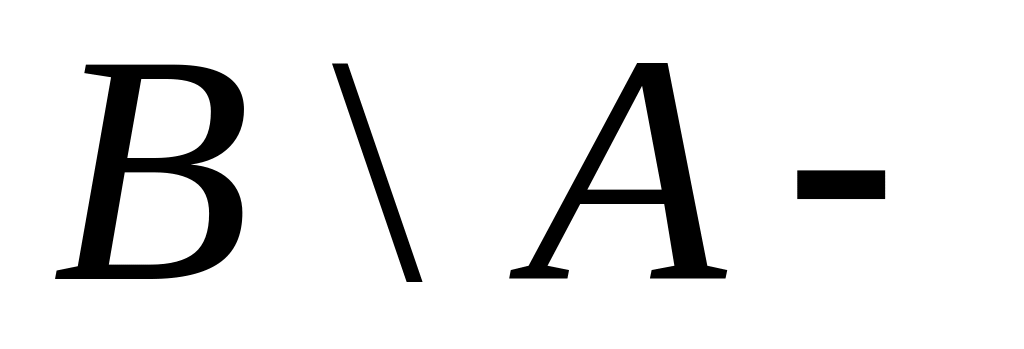 непересекающиеся множества.
непересекающиеся множества.Пусть
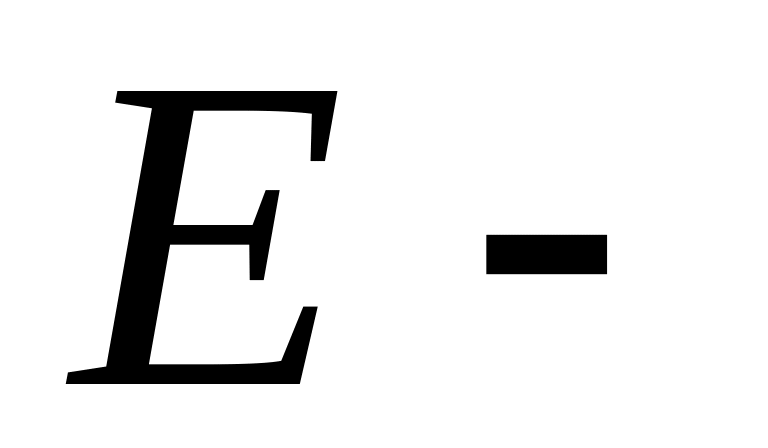 множество зоологических объектов
(универсальное множество),
множество зоологических объектов
(универсальное множество),
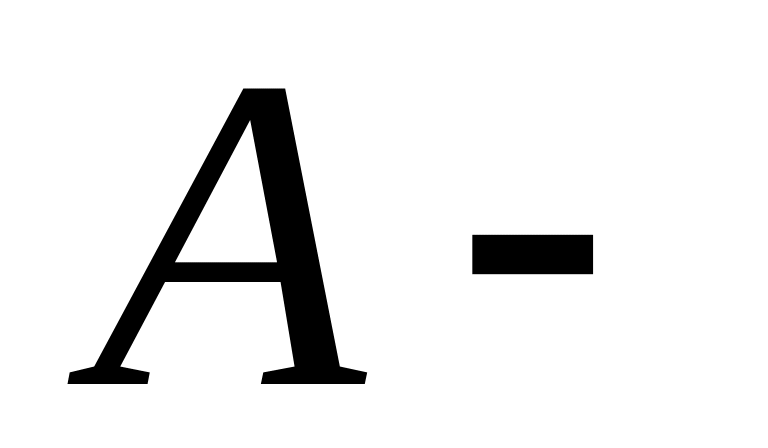 множество
обезьян,
множество
обезьян,
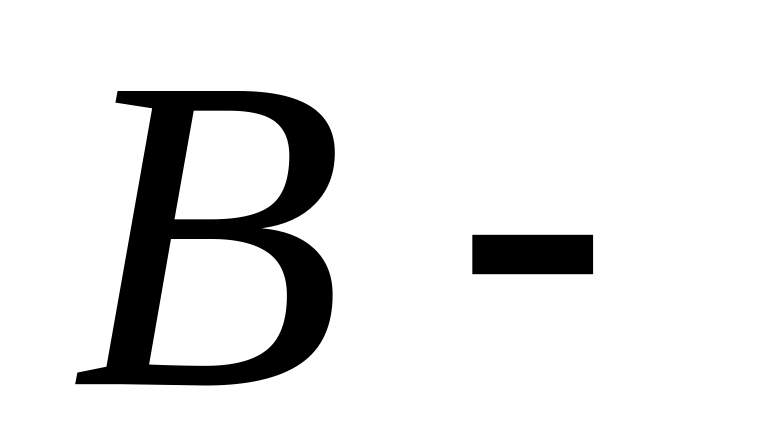 множество
млекопитающих,
множество
млекопитающих,
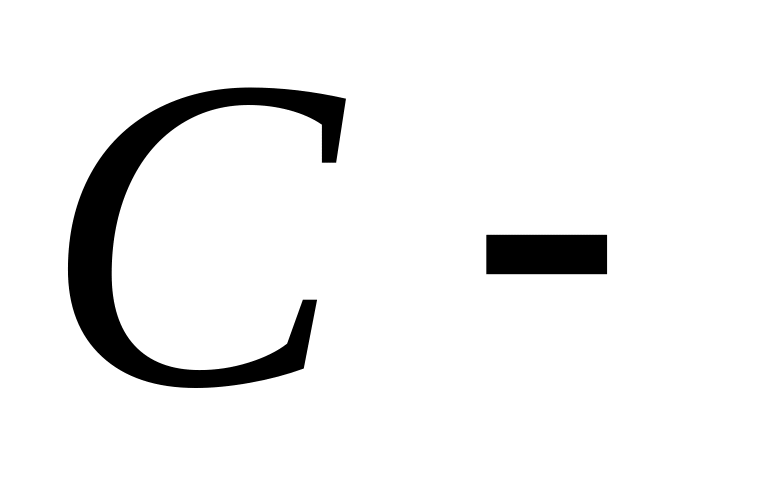 множество грызунов,
множество грызунов,
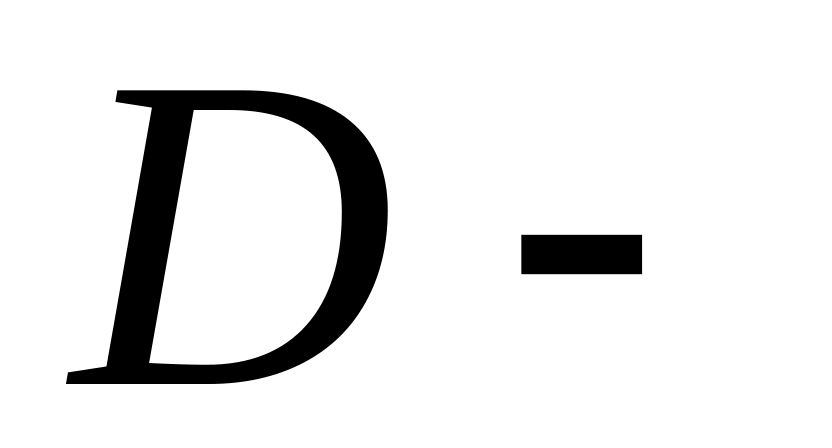 множество
насекомых,
множество
насекомых,
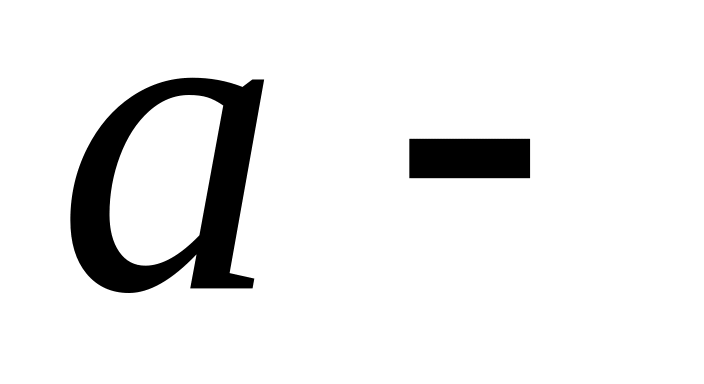 человек,
человек,
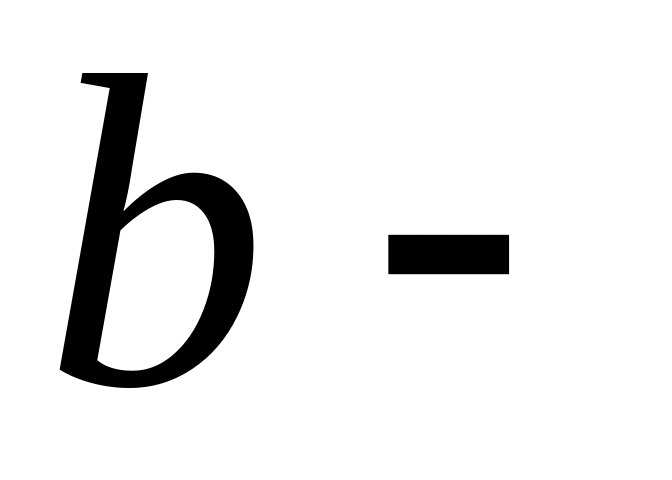 шимпанзе,
шимпанзе,
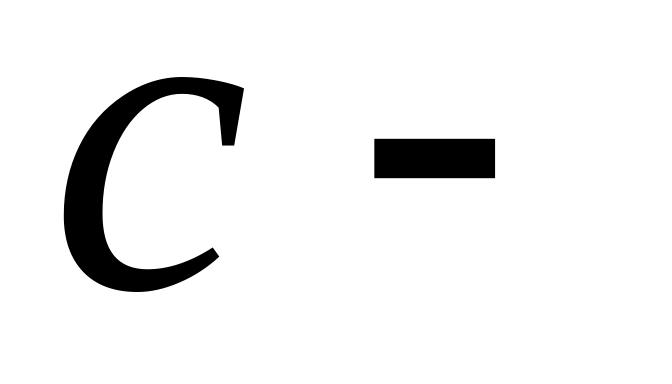 хомяк,
хомяк,
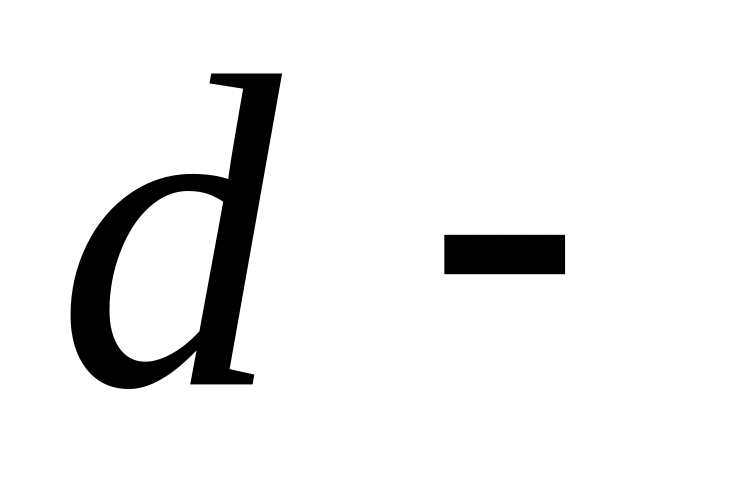 кузнечик.
Какие из утверждений верны / неверны и
почему? а)
кузнечик.
Какие из утверждений верны / неверны и
почему? а)
 ;
б)
;
б)
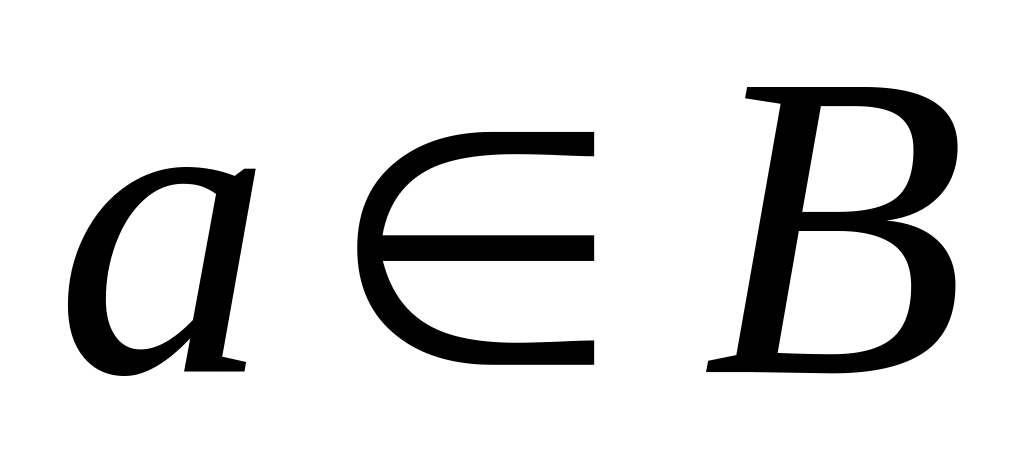 ;
в)
;
в)
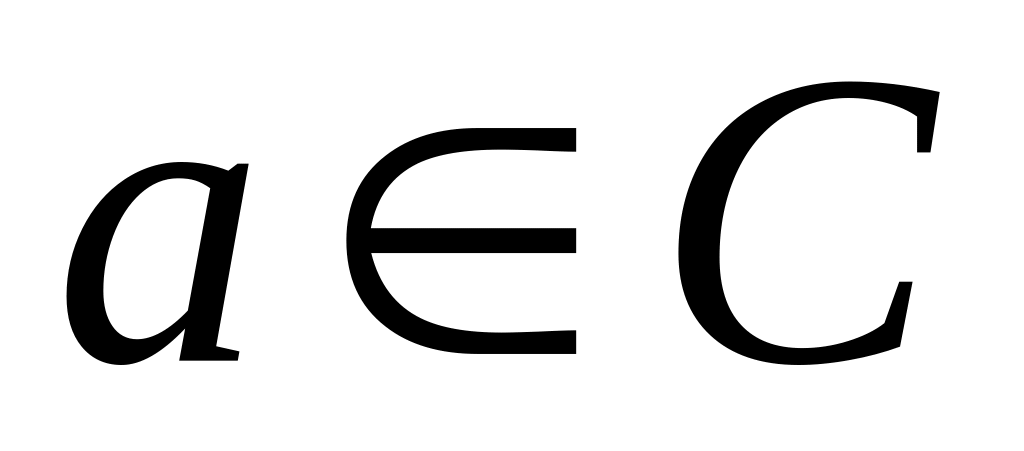 ;
г)
;
г)
 ;
д)
;
д)
 ;
е)
;
е)
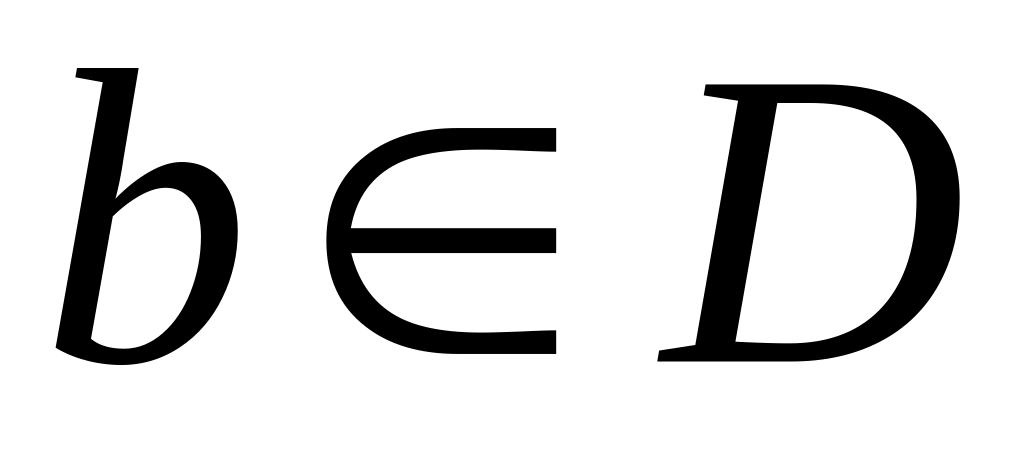 ;
ж)
;
ж)
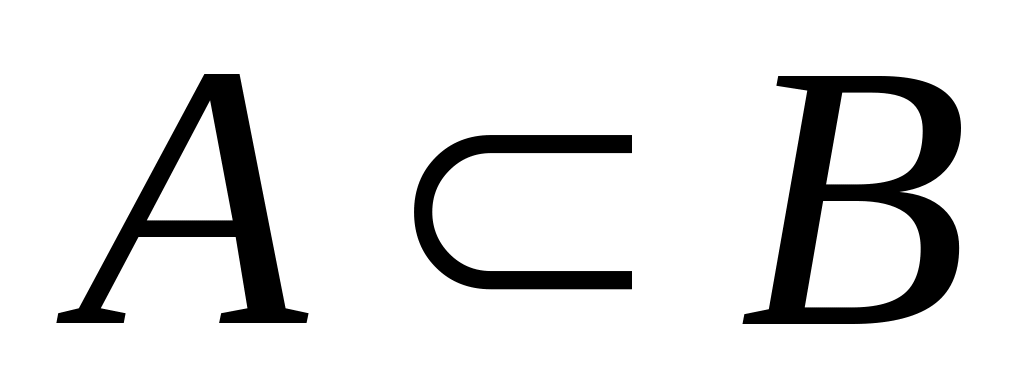 ;
з)
;
з)
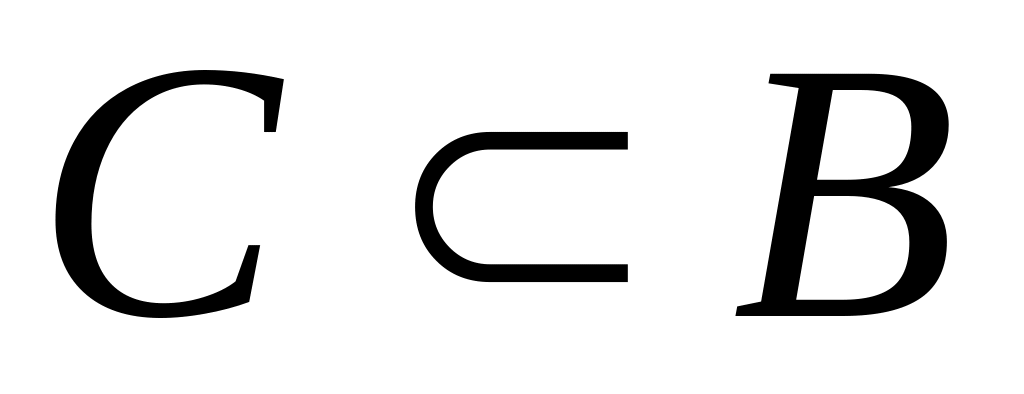 ;
и)
;
и)
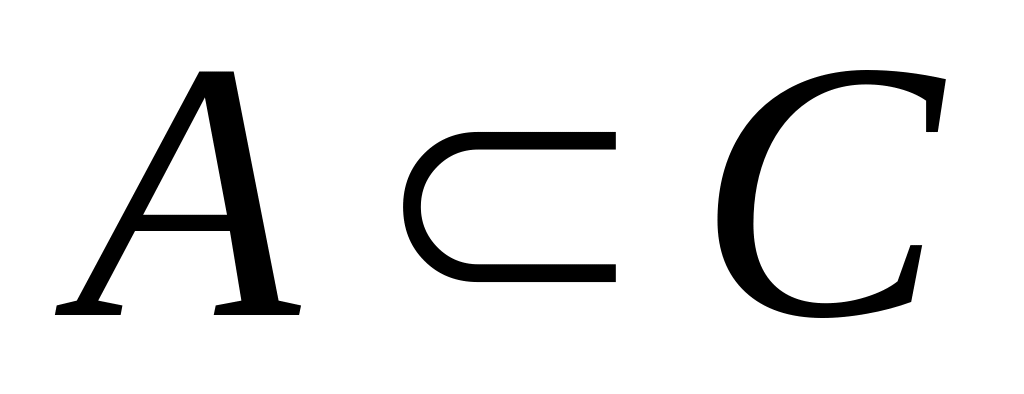 ;
к)
;
к)
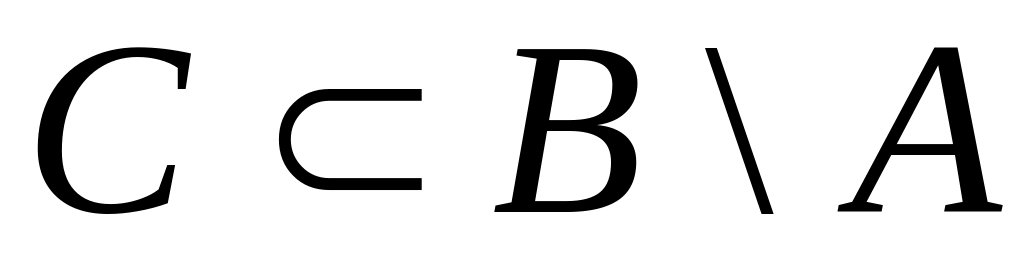 ;
л)
;
л)
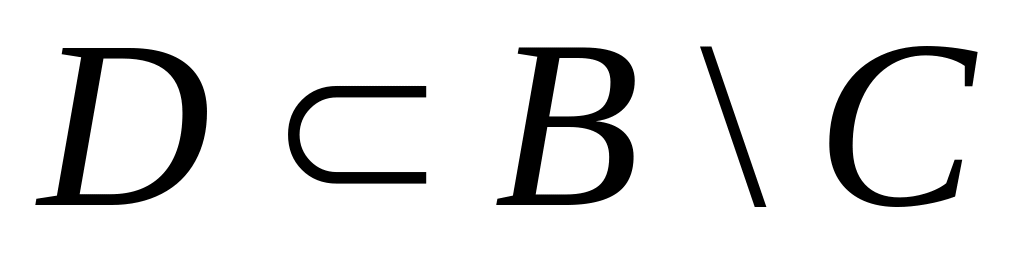 ;
м)
;
м)
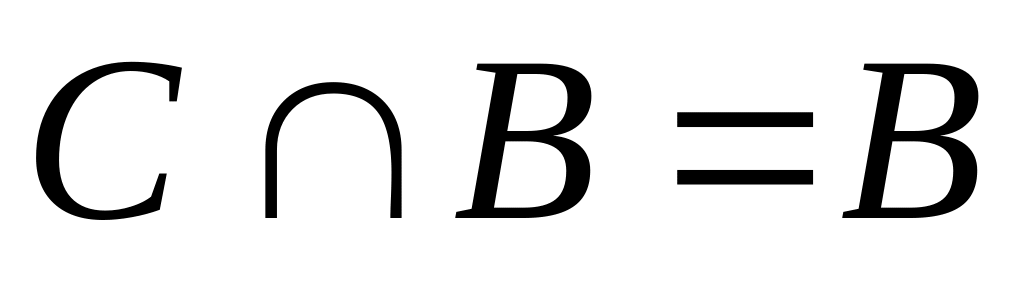 ;
н)
;
н)
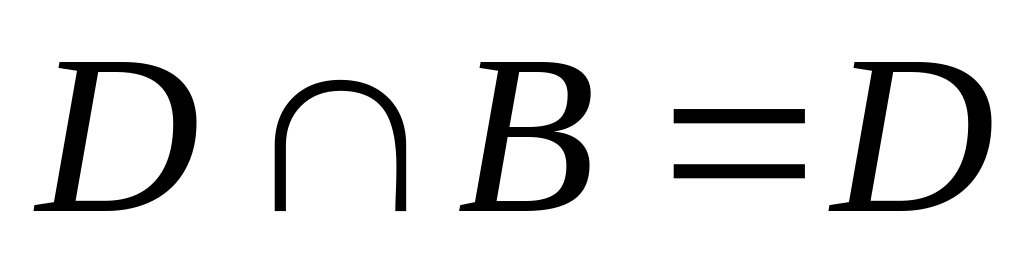 .
.В элементарной геометрии используется универсальное множество понятий
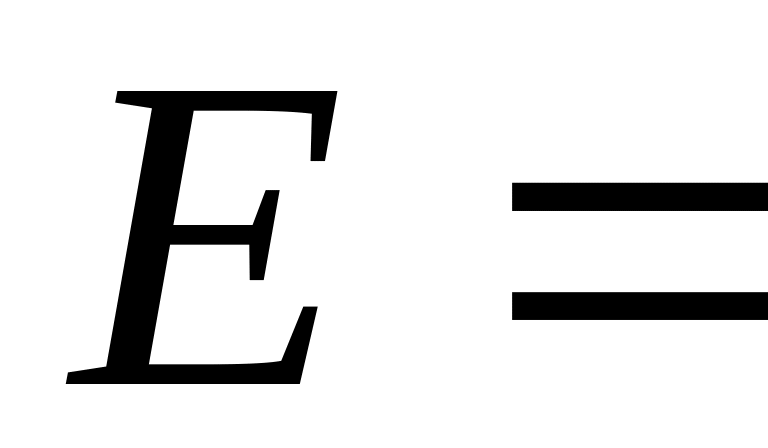 {точка,
прямая, окружность, эллипс, гипербола,
парабола, параллелограмм, прямоугольник,
ромб, квадрат, трапеция, круг, куб,
параллелепипед, призма, пирамида,
цилиндр, конус, шар}. Найдите следующие
множества:
а)
множество
линий; б)
{точка,
прямая, окружность, эллипс, гипербола,
парабола, параллелограмм, прямоугольник,
ромб, квадрат, трапеция, круг, куб,
параллелепипед, призма, пирамида,
цилиндр, конус, шар}. Найдите следующие
множества:
а)
множество
линий; б)
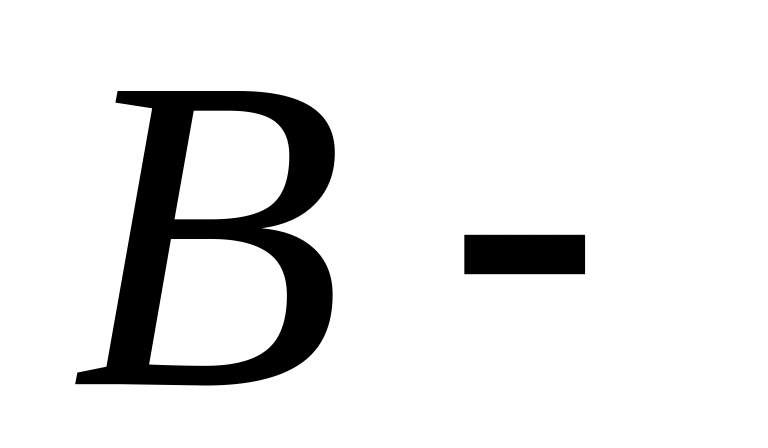 множество
фигур;
в)
множество
фигур;
в)
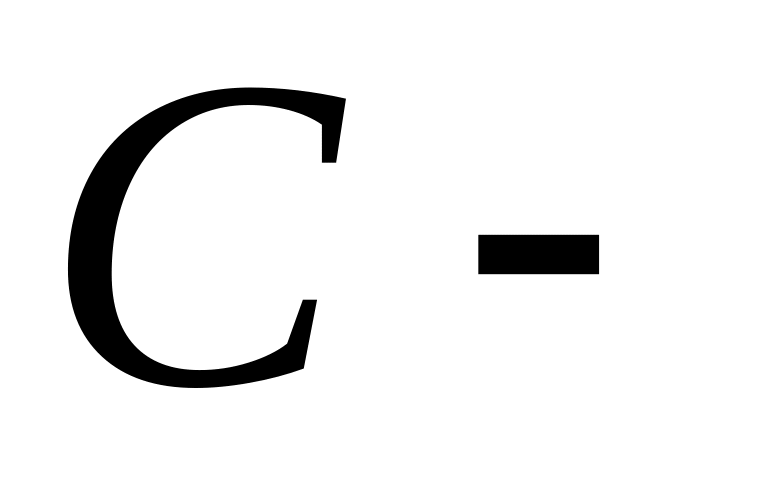 множество
тел; г)
множество
тел; г)
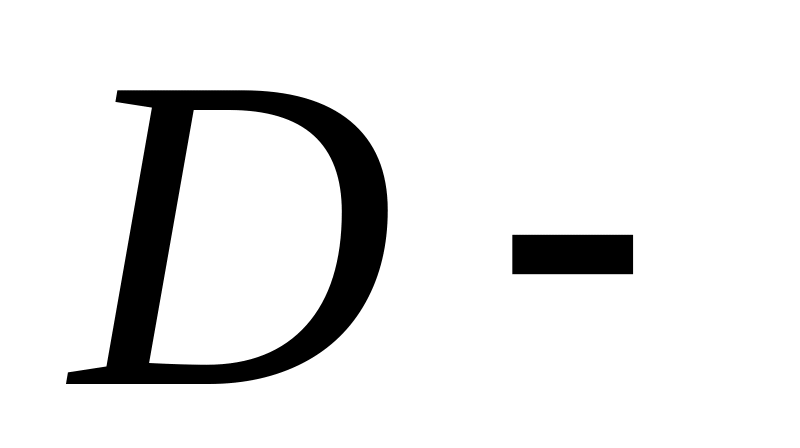 множество
четырехугольников;
д)
множество
четырехугольников;
д)
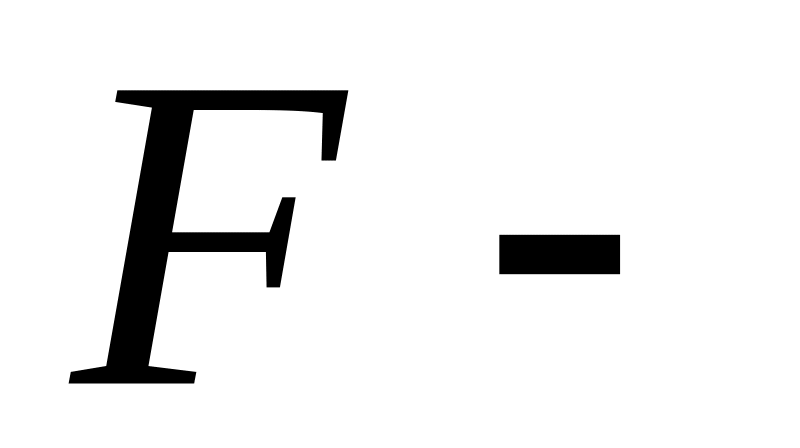 множество
тел вращения; е)
множество
тел вращения; е)
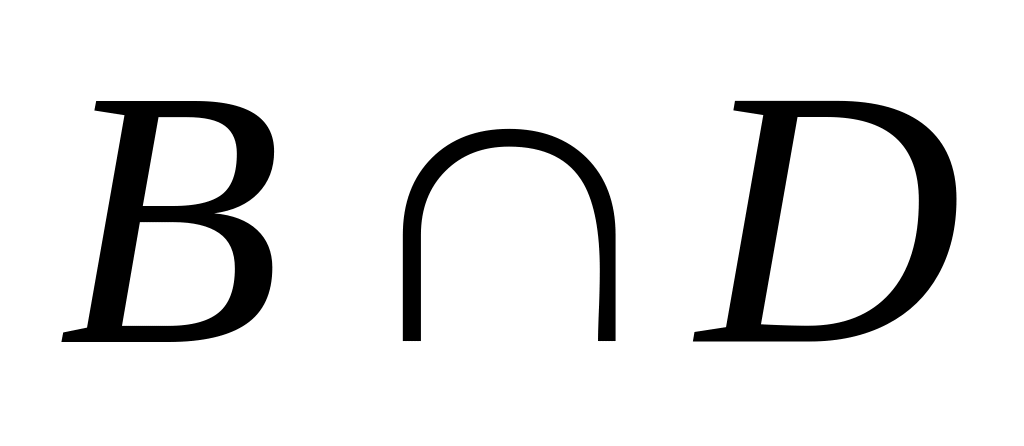 ;
ж)
;
ж)
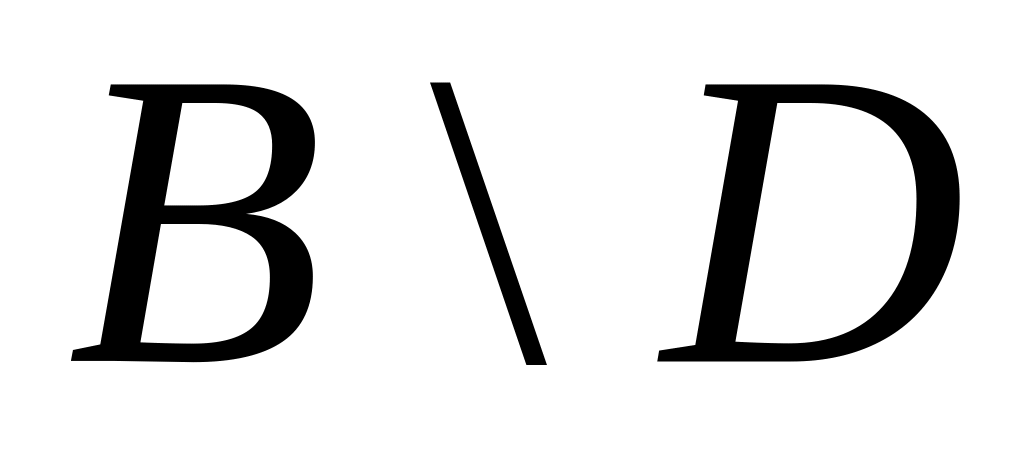 ;
и)
;
и)
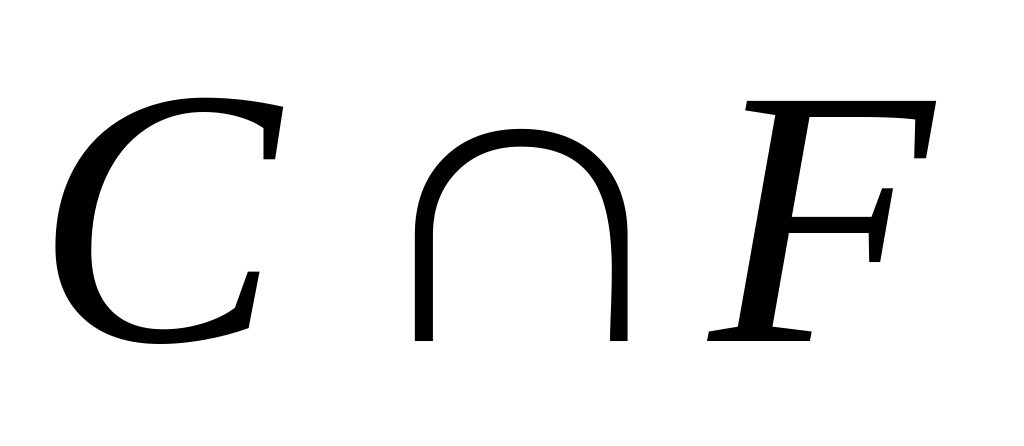 ;
к)
;
к)
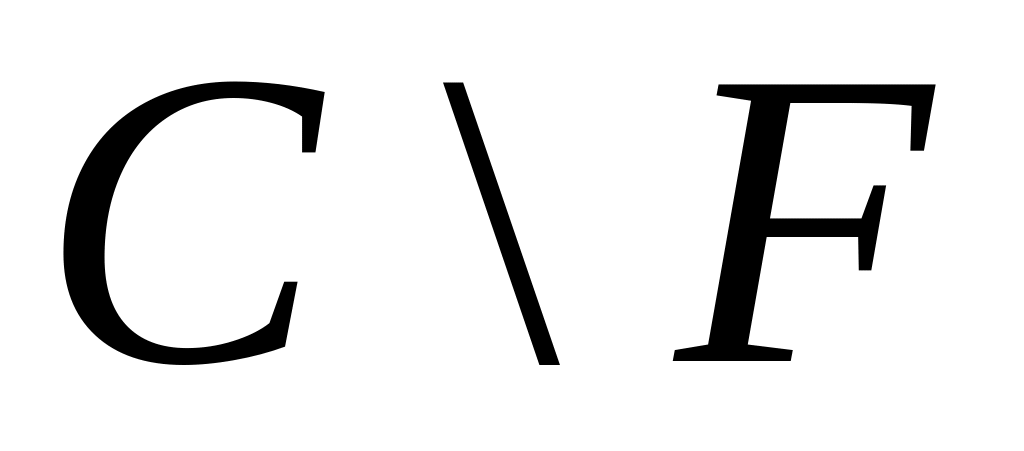 ;
л)
;
л)
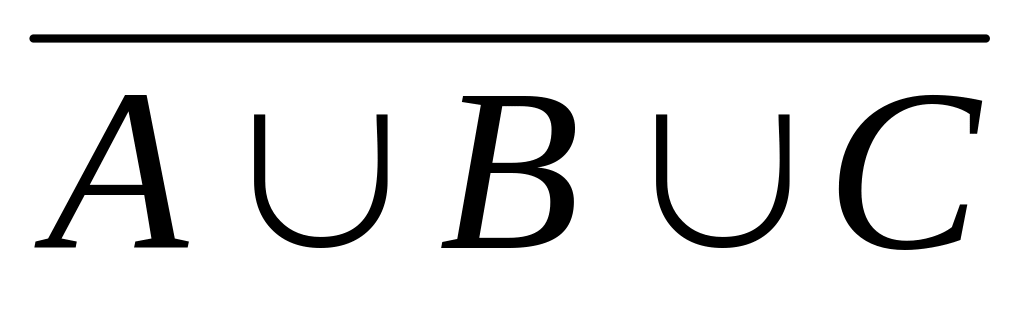 ;
м)
;
м)
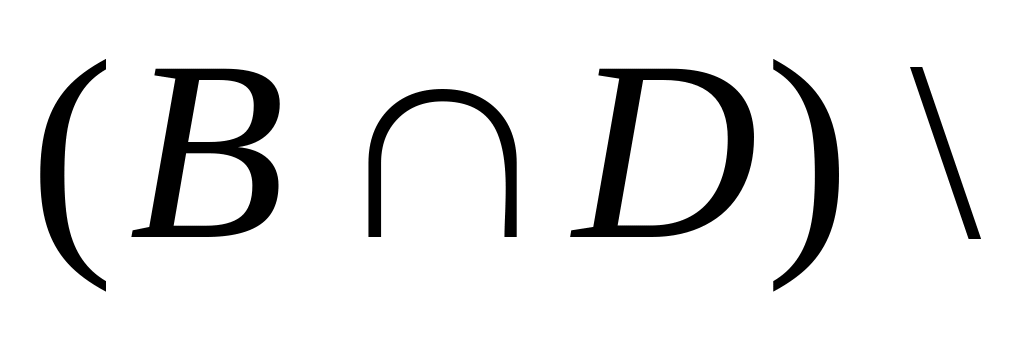 {эллипс};
н)
{эллипс};
н)
 {эллипс}.
{эллипс}.Пусть
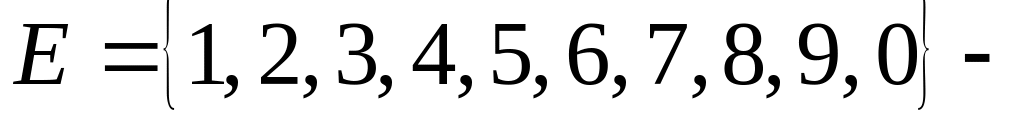 множество
цифр (универсальное множество),
множество
цифр (универсальное множество),
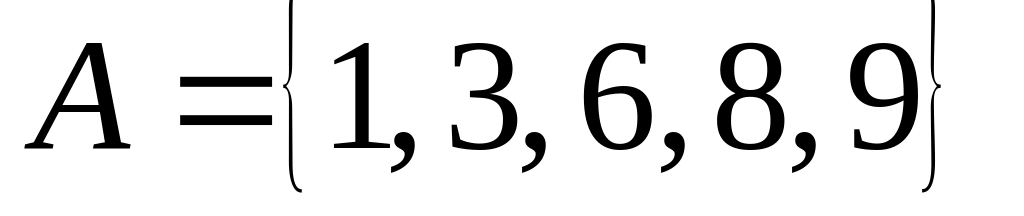 ,
,
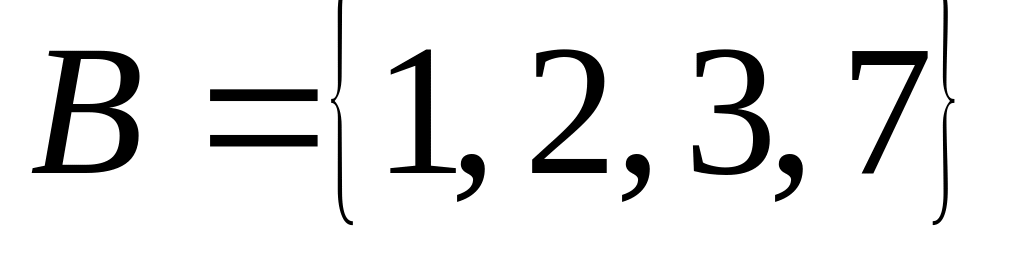 .
Найти множества:
а)
;
б)
;
в)
;
г)
.
Найти множества:
а)
;
б)
;
в)
;
г)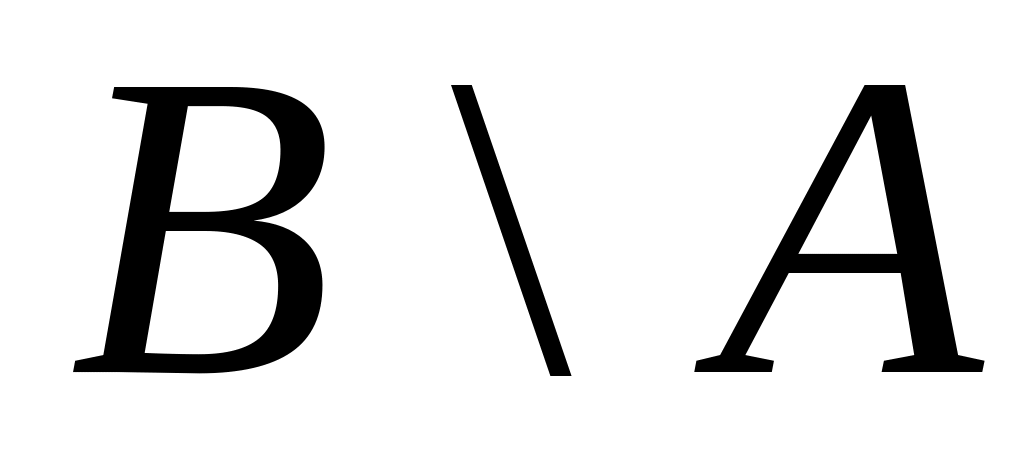 ;
д)
;
д)
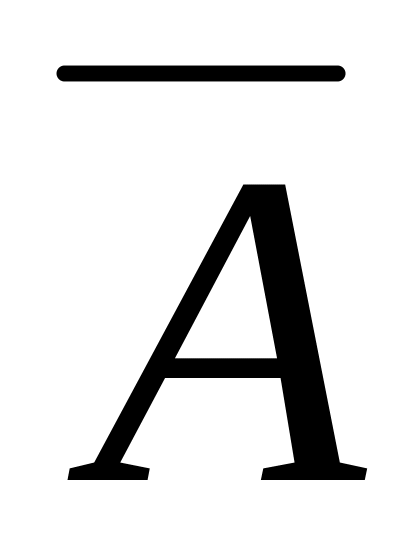 ;
е)
;
е) ;
ж)
;
ж)
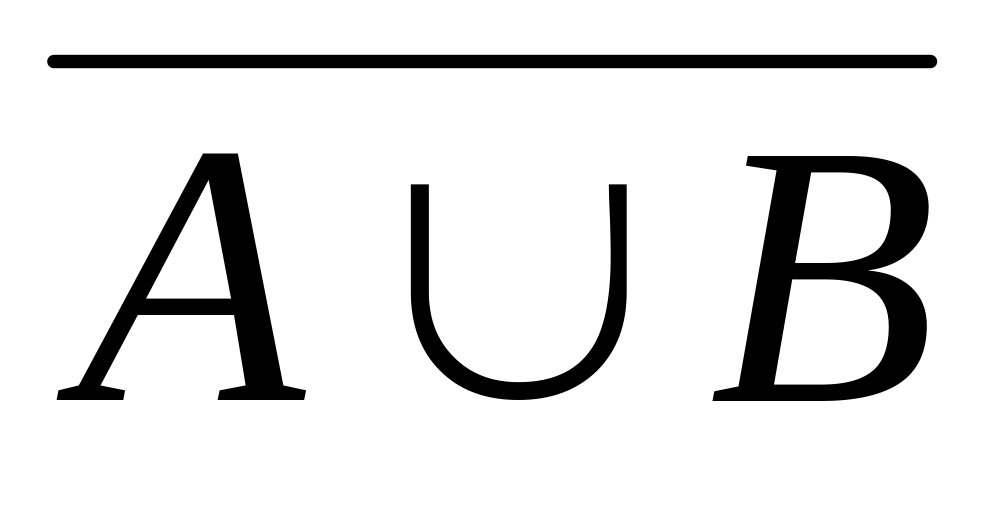 ;
з)
;
з)
Пусть
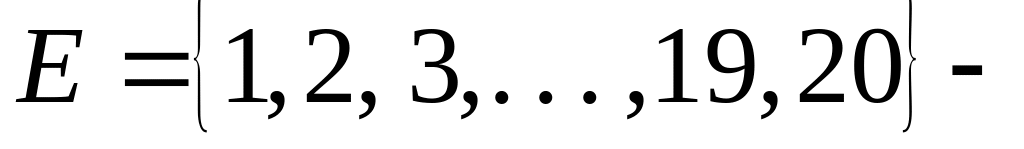 множество
первых 20 натуральных чисел (универсальное
множество),
множество
четных чисел;
множество
чисел, кратных 3;
множество
чисел, кратных 5;
множество
первых 20 натуральных чисел (универсальное
множество),
множество
четных чисел;
множество
чисел, кратных 3;
множество
чисел, кратных 5;
 множество
чисел, кратных 7. Найти множества:
а)
;
б)
множество
чисел, кратных 7. Найти множества:
а)
;
б)
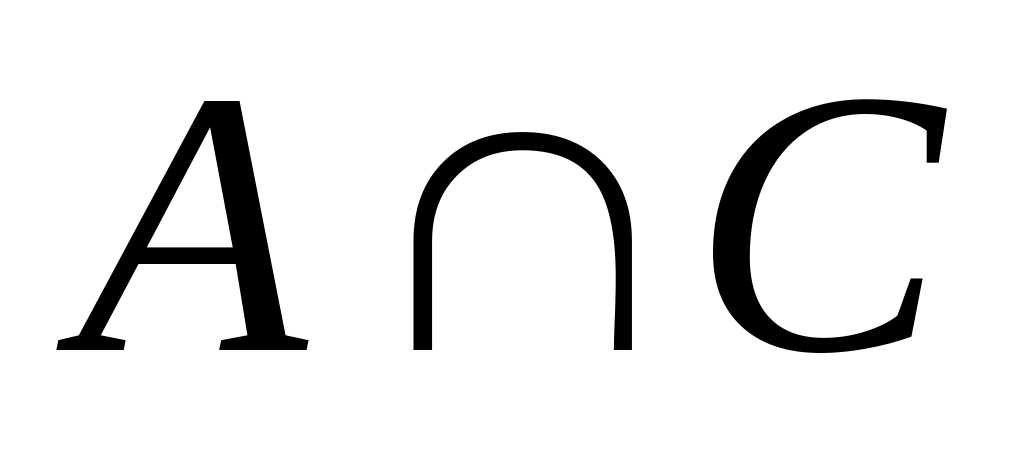 ;
в)
;
в)
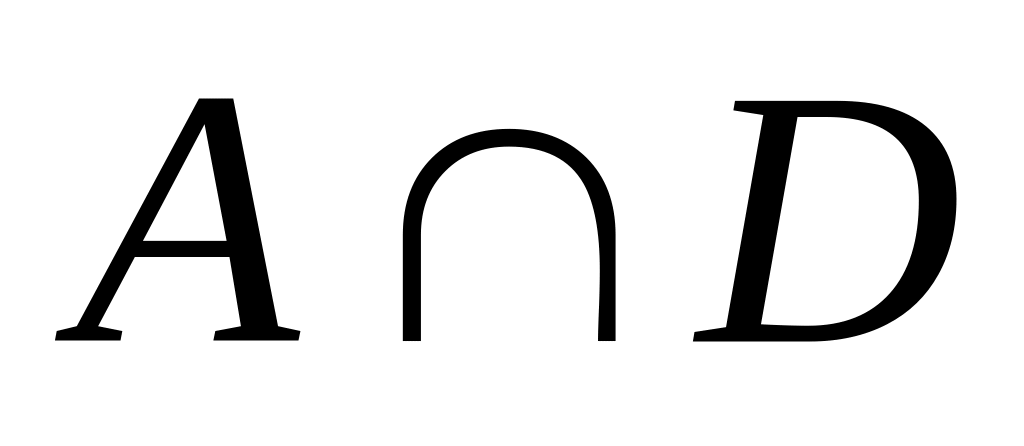 ;
г)
;
г)
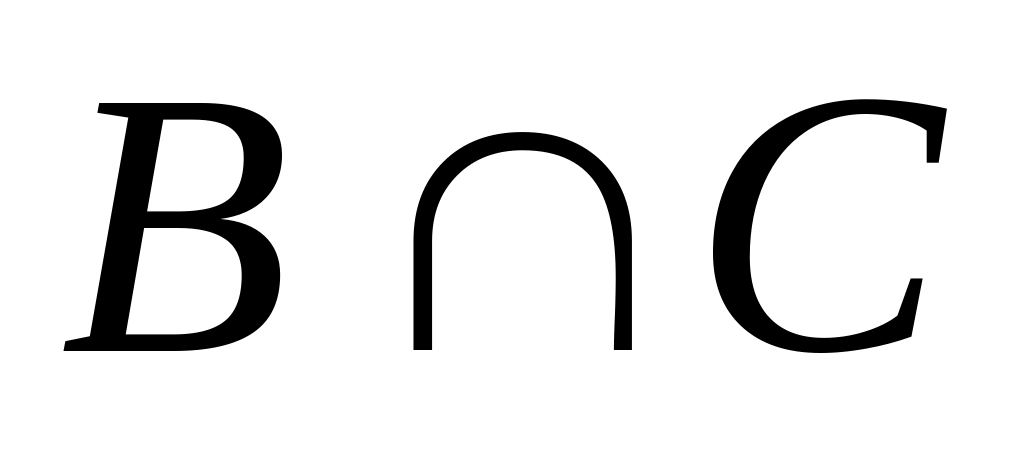 ;
д)
;
д)
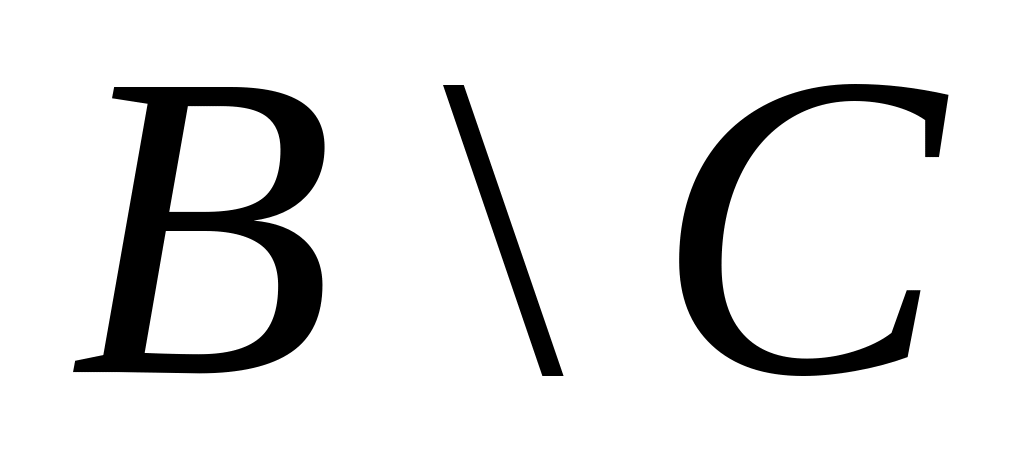 ;
е)
;
е)
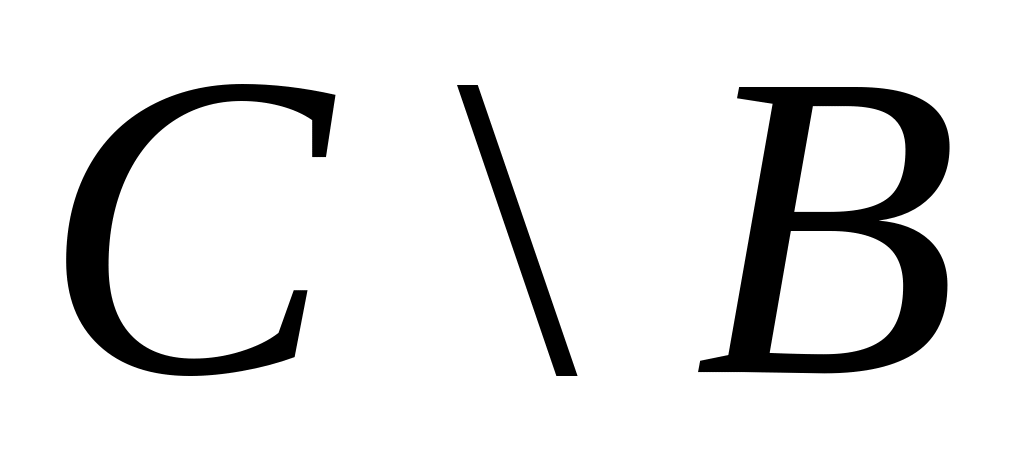 ;
ж)
;
з)
;
и)
;
ж)
;
з)
;
и)
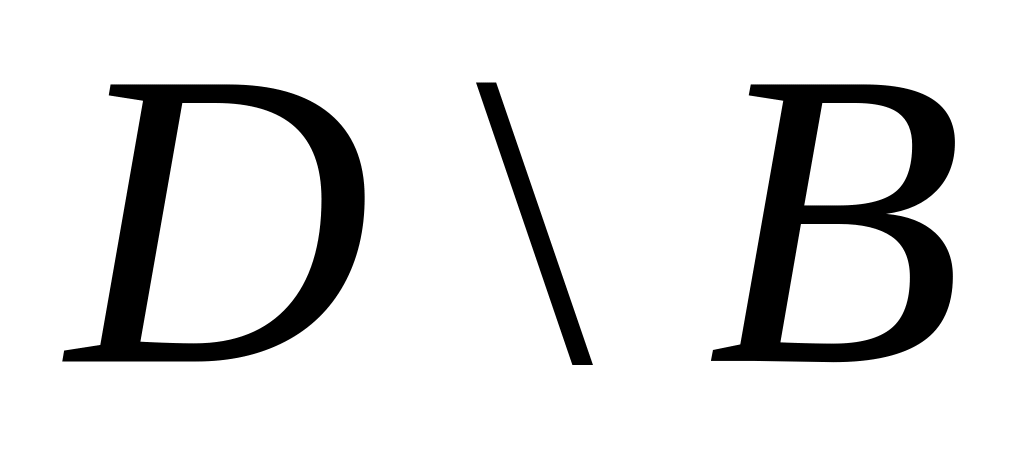 .
.Даны два множества вещественных чисел
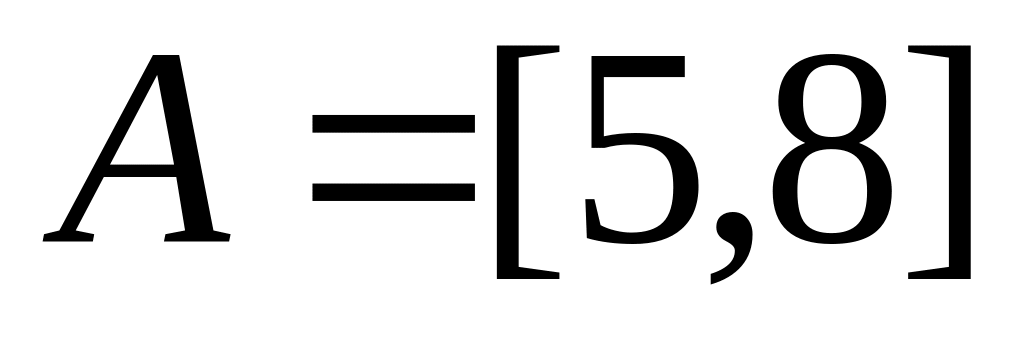 и
и
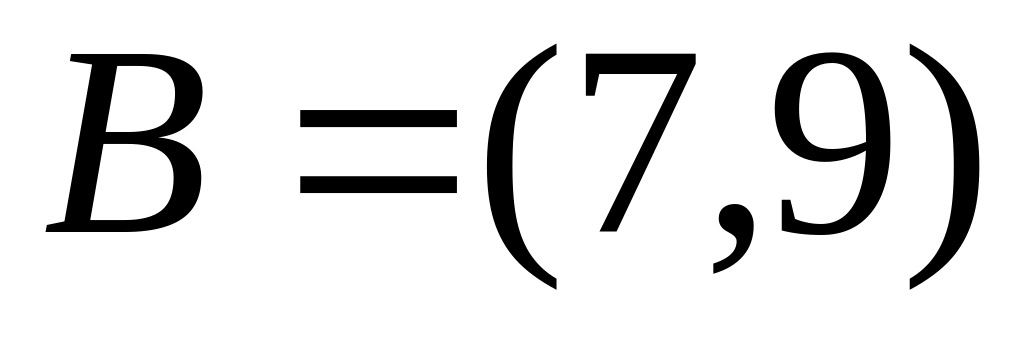 .
Найти множества:
,
,
,
,
.
Найти множества:
,
,
,
,
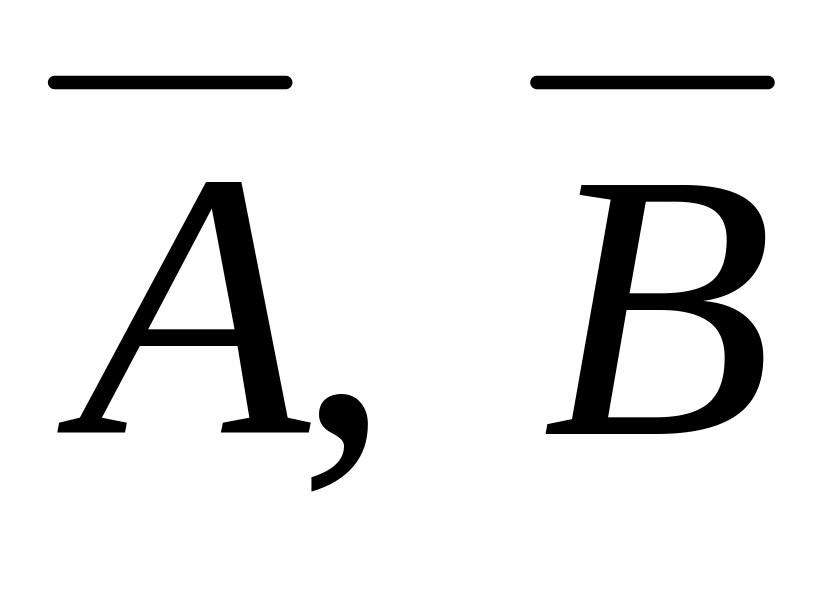 ,
,
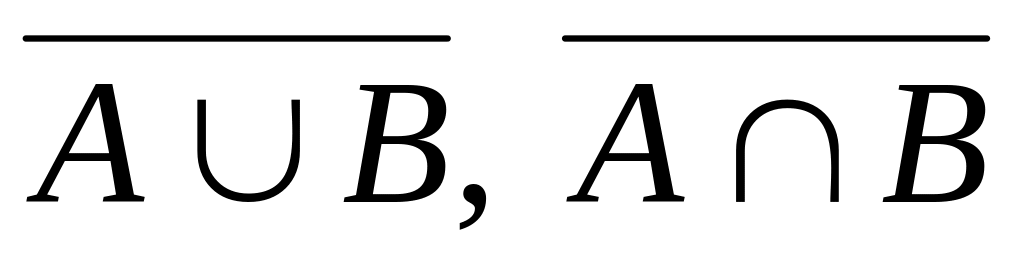 .
.
Для проведения статистического контроля выбрана студенческая группа (универсальное множество ), с именами студентов: Аня, Вика, Галя, Денис, Дима, Зоя, Иван, Игорь, Лена, Маша, Наташа, Нина, Николай, Олег, Роман, Света, Сергей, Федя, Тарас, Тимофей, Яков. Известно, что Аня, Галя, Зоя, Игорь, Маша, Николай, Олег, Роман, Яков имеют возраст до 20 лет; Вика, Лена, Сергей – отличники; Галя, Денис, Игорь, Маша, Николай учатся на 4 и 5; Нина, Света, Федя имеют двойки. Найти следующие множества:
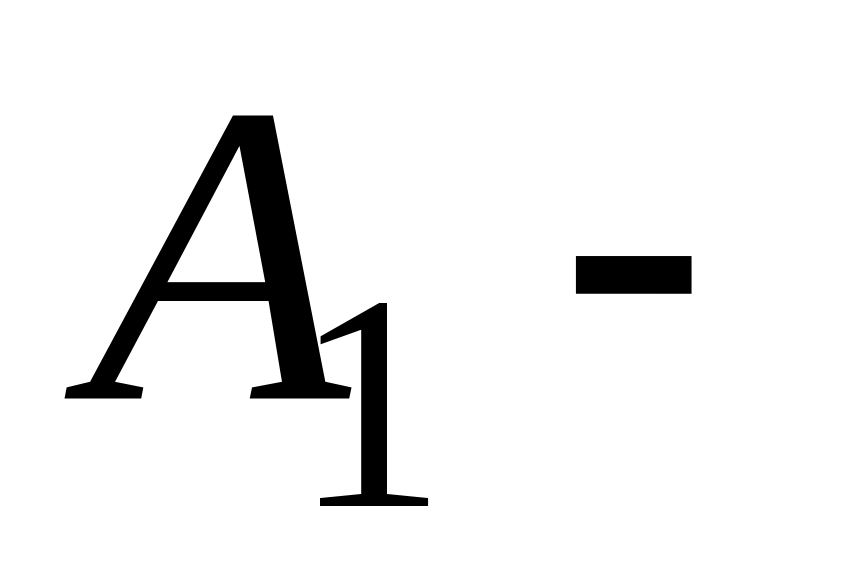 множество
девушек старше 20 лет;
множество
девушек старше 20 лет;
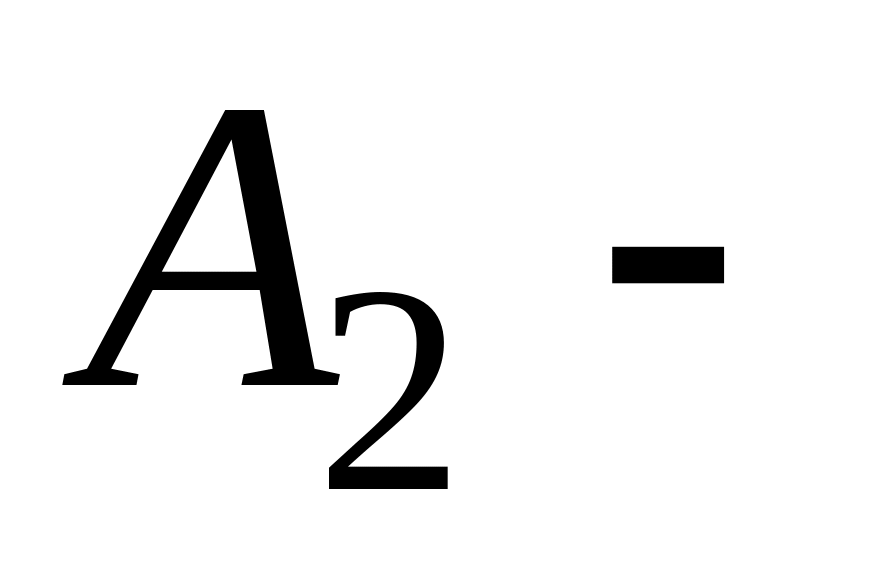 множество
юношей старше 20 лет;
множество
юношей старше 20 лет;
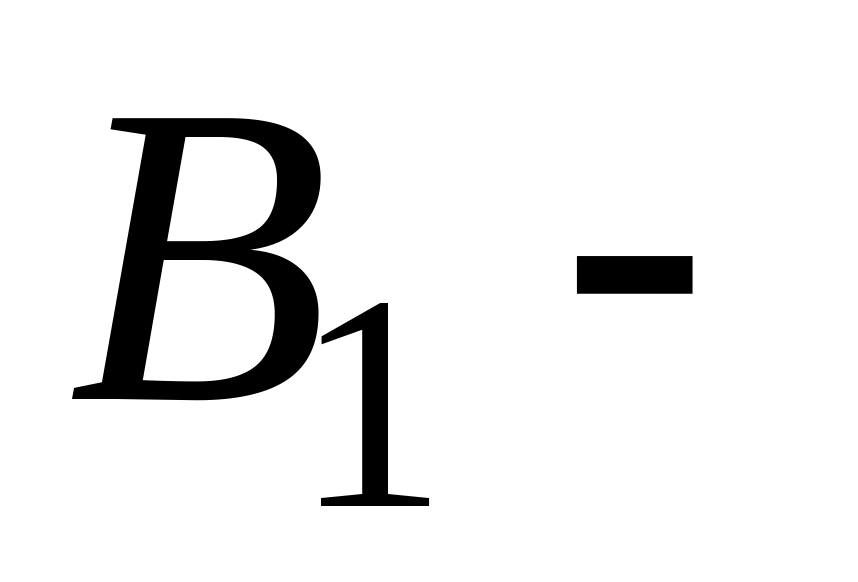 множество
девушек, не имеющих двоек;
множество
девушек, не имеющих двоек;
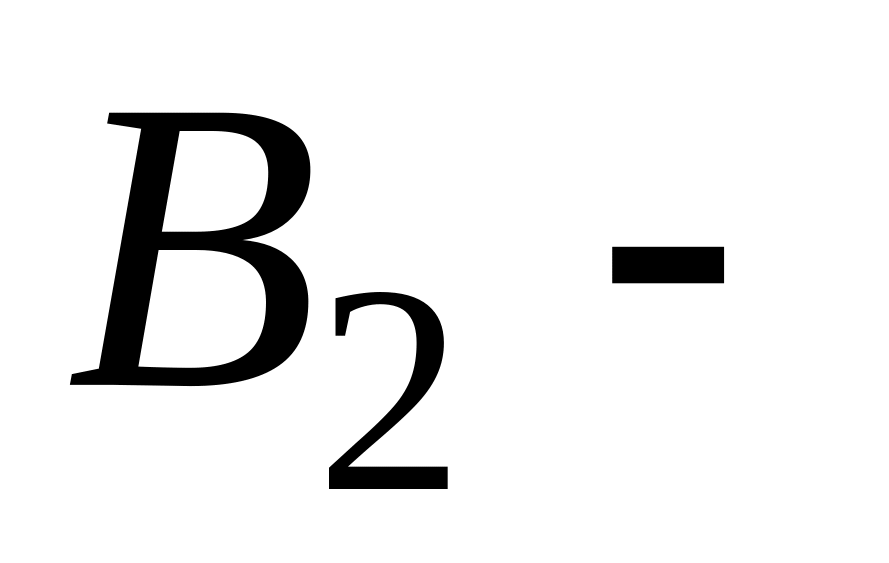 множество
юношей, не имеющих двоек;
множество
юношей, не имеющих двоек;
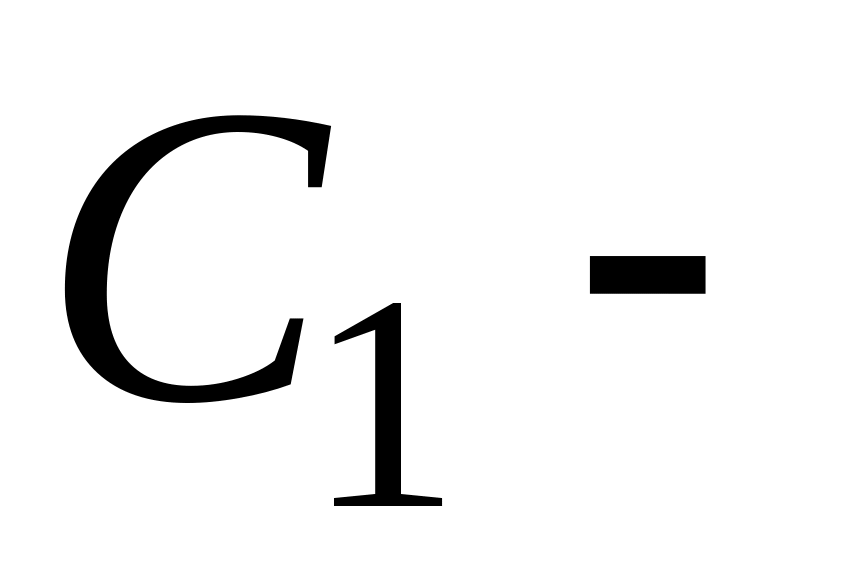 множество
отличников старше 20 лет;
множество
отличников старше 20 лет;
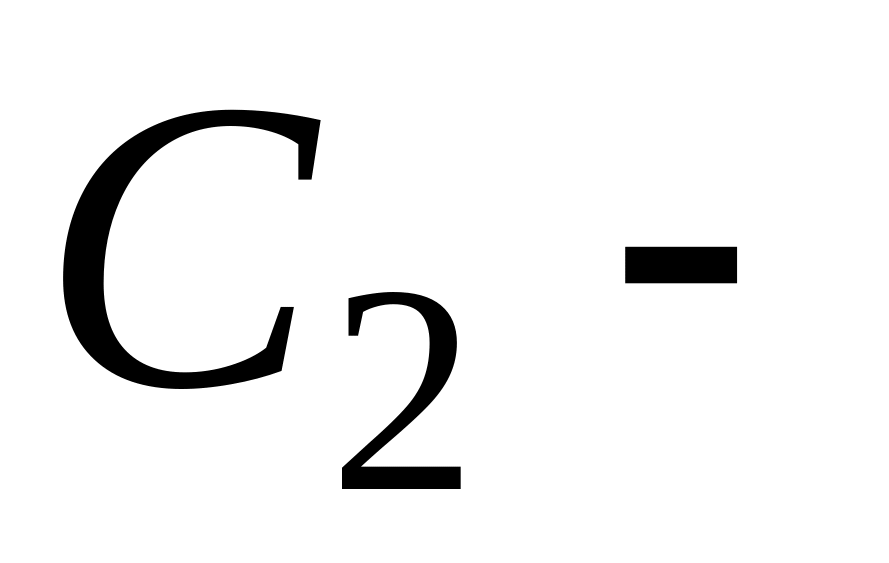 множество
отличников моложе 20 лет;
множество
отличников моложе 20 лет;
 множество
неуспевающих студентов старше 20 лет;
множество
неуспевающих студентов старше 20 лет;
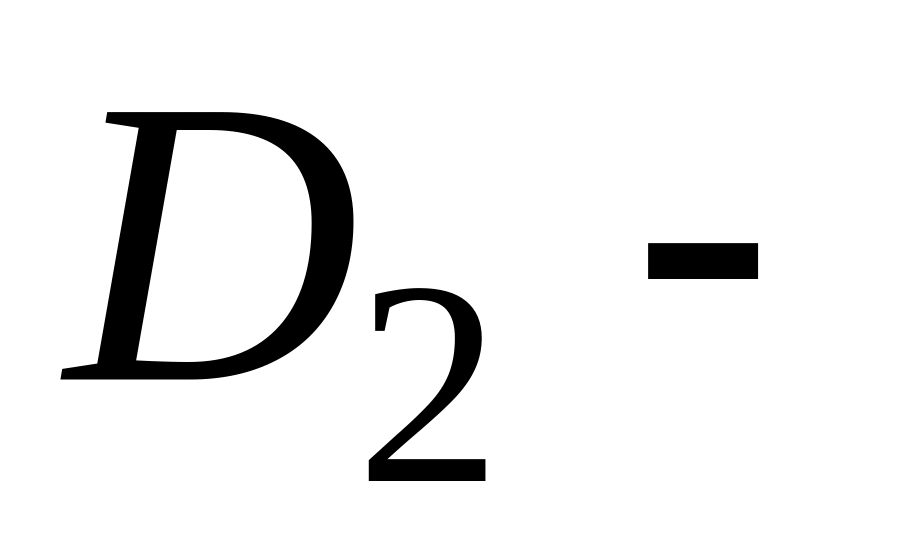 множество
неуспевающих студентов моложе 20 лет;
множество
«троечников»;
множество
неуспевающих студентов моложе 20 лет;
множество
«троечников»;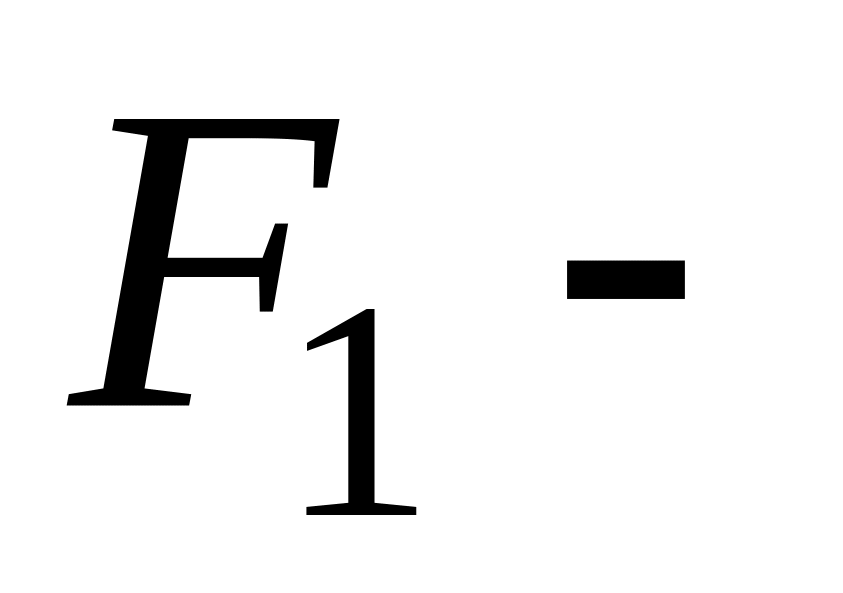 множество
«троечников» старше 20 лет;
множество
«троечников» старше 20 лет;
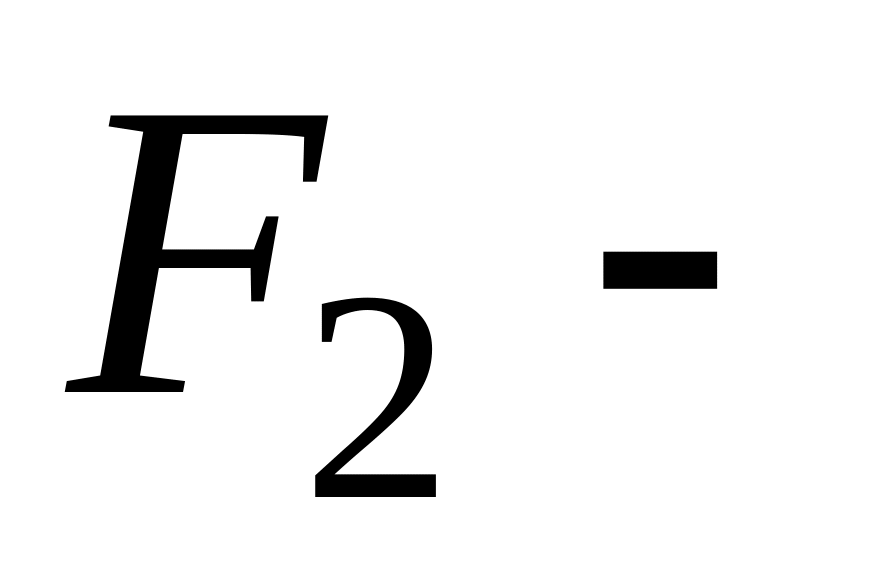 множество
«троечников» моложе 20 лет.
множество
«троечников» моложе 20 лет.
