Математическая модель преобразования электрической энергии в механическую на примере разгона проводящего кольца магнитным полем

В работе теоретически и экспериментально изучено движение проводящего кольца в изменяющемся со временем магнитном поле, создаваемом катушкой индуктивности. На основе созданной математической модели получены оптимальные соотношения между параметрами установки, обеспечивающие заданные характеристики полета кольца. Математическая модель описывается системой из трех дифференциальных уравнений, которая аналитически решена с хорошим приближением и позволяет полностью описать движение кольца. Разработан компактный вариант  э кспериментальной установки, предназначенный для демонстрации явления в любых аудиториях. С помощью экспериментальной установки получены различные экспериментальные данные, позволяющие провести сравнение теоретических выводов и результатов экспериментов. Получено удовлетворительное согласие между теорией и экспериментом.

Установка устроена следующим образом. Катушка индуктивности включена в электрическую схему, содержащую конденсатор и ключ. При разомкнутом положении ключа конденсатор заряжается от источника постоянного тока, при замкнутом положении происходит его разрядка через катушку. Металлическое кольцо помещается над катушкой таким образом, чтобы оно лежало на опоре. В момент переключения конденсатора в режим разрядки кольцо подпрыгивает вверх.

Причина явления заключается в следующем. Катушка индуктивности создает магнитное поле, которое имеет вертикальную и горизонтальную составляющие. Согласно закону электромагнитной индукции под действием вертикальной составляющей магнитного поля в кольце возникает Э.Д.С. и ток. Далее кольцо, являясь проводником с током, взаимодействует с горизонтальной составляющей магнитного поля и возникает действующая на кольцо сила Ампера.

Как известно, переменный ток не распределяется равномерно по сечению проводника, а оттесняется к поверхности (скин-эффект). Расчеты показывают, что на частоте работы этой установки скин-эффект проявляется при толщине проводника около 2 см. Поэтому, так как используемые проводники имеют много меньшую толщину, скин-эффектом можно пренебречь.

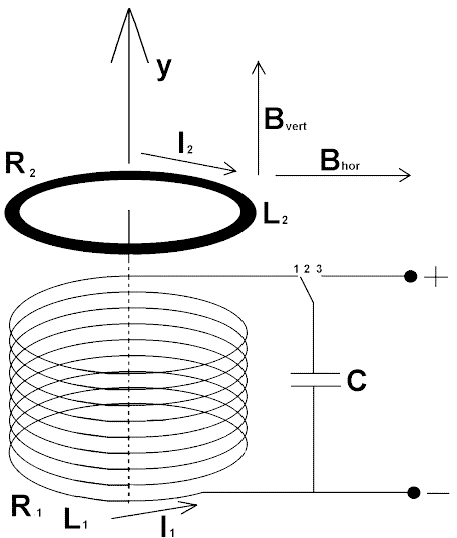
L₁ - индуктивность катушки L₂ - индуктивность кольца C - емкость конденсатора R₁ - электрическое сопротивление катушки R₂ - электрическое сопротивление кольца y - вертикальная координата кольца I₁ - ток в катушке I₂ - ток в кольце

Экспериментальные данные

- экспериментальные результаты - теоритические результаты Суммарная погрешность высоты не превышает 10 см

Зависимость высоты полета H кольца от числа витков N катушки индуктивности

Зависимость высоты полета H кольца от емкости конденсатора C

Зависимость высоты полета H кольца от напряжения зарядки конденсатора U

Зависимость высоты полета H кольца от радиуса кольца R

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОСТОГО РЕЖИМА ВОСПРОИЗВОДСТВА ПРЕДПРИЯТИЯ

Производственная функция простого режима воспроизводства предприятия

В процессе производства, с одной стороны, осуществляются капиталовложения и ввод основных производственных фондов (ОПФ) в эксплуатацию. Этим процессом обусловлено увеличение количества производственных фондов. С другой стороны, происходит уменьшение производственных фондов в результате амортизации и выбытия. Если в качестве модели движения производственных фондов принять инерционное звено первого порядка, у которого внешнее воздействие I(t) – интенсивность потока капиталовложений, S(t) – интенсивность потока амортизации и T – лаг эксплуатации производственных фондов, тогда текущая стоимость производственных фондов определяется операторным уравнением (применение метода преобразования Лапласа [5]):

,                                                       (1)

где F0 – начальная стоимость производственных фондов.

Запишем изображение процесса амортизации в виде:

,                                                         (2)

то есть амортизация пропорциональна текущей стоимости производственных фондов и составляет постоянную ее долю. Доля амортизированных фондов n – норма амортизации. Подставив реакцию A(s) в (1) и решив это уравнение относительно F(s), получим следующую зависимость накопленного количества производственных фондов от капиталовложений:

.                                                       (3)

Предположим теперь, что производственная функция зависит только от стоимости производственных фондов, то есть является однофакторной. В данном случае абстрагируемся от трудовых ресурсов и прочих параметров, так как они не влияют на окончательный результат. Запишем однофакторную динамическую производственную функцию сельхозпредприятия:

,                                                  (4)

где m – фондоотдача.

Подставив в (4) полученное выражение (3), получим зависимость интенсивности выпуска от интенсивности потока капиталовложений в операторной форме:

, ,                                           (5)

где F(s) – передаточная функция производственной функции простого режима воспроизводства предприятия.

 

Математическая модель простого режима воспроизводства предприятия

В синтезе модели отдельного предприятия будем исходить из того, что объем произведенной и реализованной продукции зависит от остаточной стоимости ОПФ, которая может увеличиваться или уменьшаться. Она возрастает в зависимости от капиталовложений и уменьшается в результате амортизации и выбытия некоторой части основных средств. Следовательно, рост объемов выпуска может быть обеспечен в том случае, если капиталовложения превышают количество изношенных ОПФ, тогда и текущая их стоимость увеличивается. При снижении стоимости ОПФ рост объема выпуска может быть достигнут за счет повышения фондоотдачи, то есть влияния научно-технического прогресса. Эти явления отражает модель производства в виде однофакторной динамической производственной функции.

Капиталовложения слагаются из централизованных средств I(t) и отчислений от дохода U(t). Предположим, что отчисления регламентируются нормативом a < 1. Тогда функциональную структуру развития предприятия можно представить в виде модели с положительной обратной связью, состоящей из двух звеньев. Усилительное звено 2 отражает процесс выделения собственных капиталовложений при нормативе отчислений от объема реализации продукции a. Вместе с централизованными капиталовложениями собственные средства воздействуют на звено производства 1, изменяя стоимость ОПФ и объем дохода от реализации продукции X(t) в виде динамической производственной функции.  

Чтобы найти передаточную функцию системы необходимо разрешить следующую систему уравнений относительно X(s):

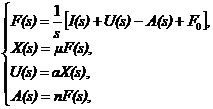                                           (6)  

где n – норма амортизации,

       F0 – начальное значение стоимости ОПФ,

       m – фондоотдача в единицах измерения остаточной стоимости ОПФ,

       a – норматив отчислений в фонд развития производства,

       n – норма амортизации.

В результате получим:

,                                  (7)           

где первое слагаемое – вынужденная, а второе – свободная составляющая; x0 – начальное значение интенсивности производства и реализации продукции. Передаточная функция системы равна .          

Заключение

Получена математическая модель простого режима воспроизводства предприятия. Данная модель развития предприятия пригодна для анализа сложных систем,  в которые эта модель может входить как составной элемент.

Задание 23

Проблемы, возникающие в системах, и возможные пути их решения:

• Мышечная система:

1. Проблема – после длительной нагрузки нехватка сил. Решение – возможно помощь стимуляторов.

2. Проблема – нерасчет сил и травма мышц. Решение – лечебные мази, массаж.

• Пушка Гаусса– централизованное управление.

1. Проблема – большой расход энергии. Решение – увеличение количества емкости конденсаторов или поиск надежного и переносного источника питания.

2. Проблема - низкий КПД установки. Решение – использование многоступенчатой системы разгона снаряда.

3. Проблема (следует из первых двух) – большой вес и габариты установки, при её низкой эффективности. Решение – еще не придумано.

• Магазин сотовой техники – централизованное управление.

1. Проблема – нехватка специалистов. Решение – поиск более знающих сотрудников.

2. Проблема – иногда возникает проблема в скорости обслуживания. Решение – увеличение количества работников.

Задание 24

Задачи выбора для магазина:

Основной задачей выбора для покупателя является проблема выбора между товарами. Из-за большого количества сотовой техники у покупателя возникает разногласие в собственных желаниях. В этом выборе покупателю помогают продавцы-консультанты, они помогают определится покупателю с товаром и подобрать то что ему нужно.