V. Методические указания по выполнению контрольной работы

ЗАДАЧА 1 (вариант …). Найти пределы функций, не пользуясь правилом Лопиталя в пунктах а) – г), с использованием правила Лопиталя в пункте д).

Решение. а)

Имеем неопределенность вида , так как пределы числителя и знаменателя равны нулю, т. е. . Следовательно, теорему о пределе частного здесь применить нельзя. Для раскрытия этой неопределенности разложим числитель и знаменатель на множители:

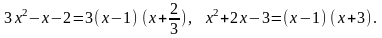
Таким образом,

Ответ:

б)

Имеем неопределенность вида , так как пределы числителя и знаменателя равны нулю. Для раскрытия этой неопределенности умножим числитель и знаменатель дроби на выражение, сопряженное числителю, т. е. на . Таким образом,

Ответ: -3.

в)

Имеем неопределенность вида 1¥, так как

Преобразуем функцию так, чтобы использовать второй замечатель-

ный предел

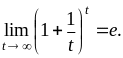
Таким образом,

Ответ: .

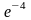г)

Имеем неопределенность вида . Для раскрытия этой неопределенности воспользуемся формулой и первым замечательным пределом

Таким образом,

Ответ: 2.

д)

Имеем неопределенность вида 0⁰. Для раскрытия этой неопределенности преобразуем исходную функцию, воспользовавшись равенством

Таким образом,

В показателе степени имеем неопределенность вида . Для раскрытия этой неопределенности воспользуемся правилом Лопиталя:

Окончательно имеем:

Ответ: 1.