Контрольная электростатика
..doc
МИНИСТЕРСТВО
РЕСПУБЛИКИ БЕЛАРУСЬ
институт
Зачётная книжка №
Контрольная работа №2
по курсу
«Физика»
Слушателя курса,
учебной группы №
факультета заочного обучения
Белоуса
Проверил: преподаватель кафедры
Минск 2010
Содержание
-
Задача №301………………………………………………..3
-
Задача №319…………………………………………..……5
-
Задача №328…………………………………………..……6
-
Задача №340…………………………………………..……7
-
Задача №401……………………………………………..…9
-
Задача №416…………………………………………….…11
-
Задача №452……………………………………………….12
-
Задача №466……………………………………………….13
-
Литература…………………………………………………14
Задача № 301
Точечные
заряды
![]() мкКл и
мкКл и
![]() мкКл находятся на расстоянии
мкКл находятся на расстоянии
![]() см друг друга. Определить напряженность
поля в точке, удаленной на
см друг друга. Определить напряженность
поля в точке, удаленной на
![]() см
от первого и
см
от первого и
![]() см
от второго заряда.
см
от второго заряда.
|
Дано:
|
Решение.
|
|
Найти: Е-? |
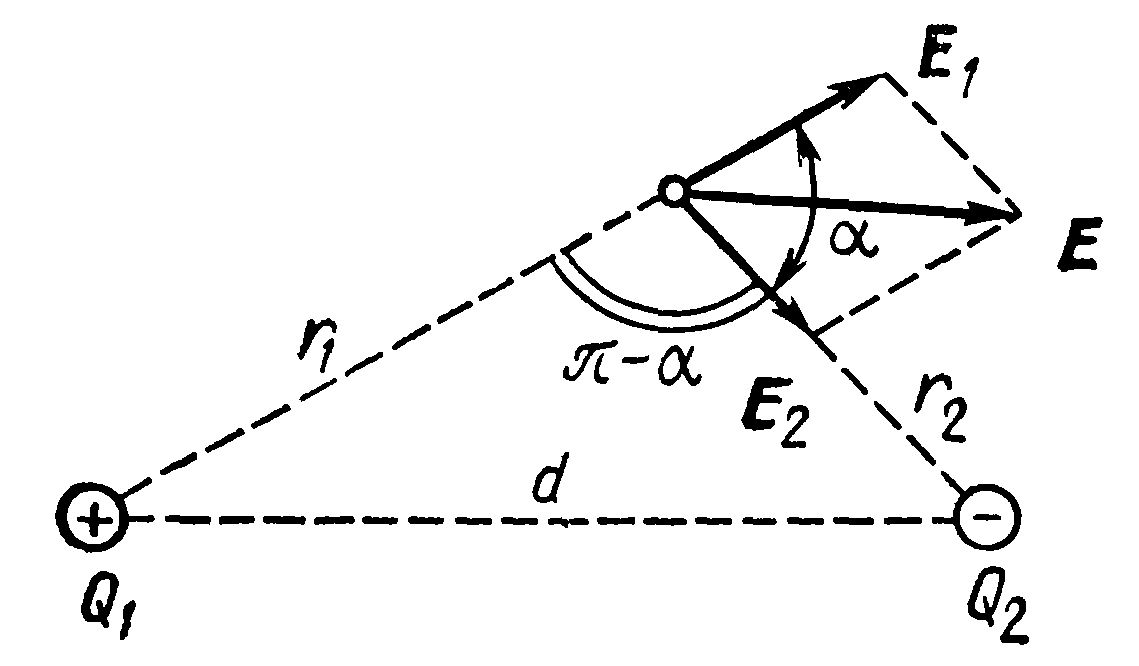
Согласно
принципу суперпозиции электрических
полей, каждый заряд создает поле
независимо от присутствия в пространстве
других зарядов. Поэтому напряженность
![]() электрического поля в искомой точке
может быть найдена как векторная сумма
напряженностей
электрического поля в искомой точке
может быть найдена как векторная сумма
напряженностей
![]() и
и
![]() полей, создаваемых каждым зарядом в
отдельности:
полей, создаваемых каждым зарядом в
отдельности:
![]()
Напряженности электрического поля, создаваемого в вакууме первым и вторым зарядами, соответственно равны;
![]() ;
;
![]()
Вектор
![]() направлен по силовой линии от заряда
направлен по силовой линии от заряда
![]() ,
так как заряд
,
так как заряд
![]() ;
вектор
;
вектор
![]() направлен также по силовой линии, но к
заряду
направлен также по силовой линии, но к
заряду
![]() ,
так как
,
так как![]() .
.
Модуль
вектора
![]() найдем по теореме косинусов:
найдем по теореме косинусов:
![]()
где
угол а может быть найден из треугольника
со сторонами
![]() :
:
![]()
Значит,
![]()
Следовательно:
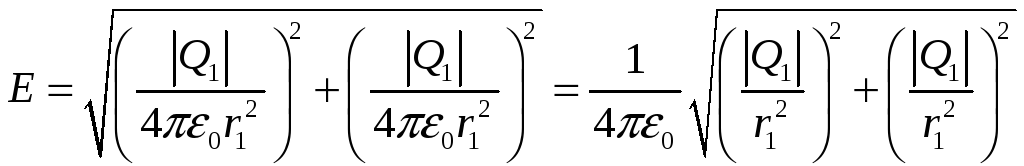
Анализ размерности:
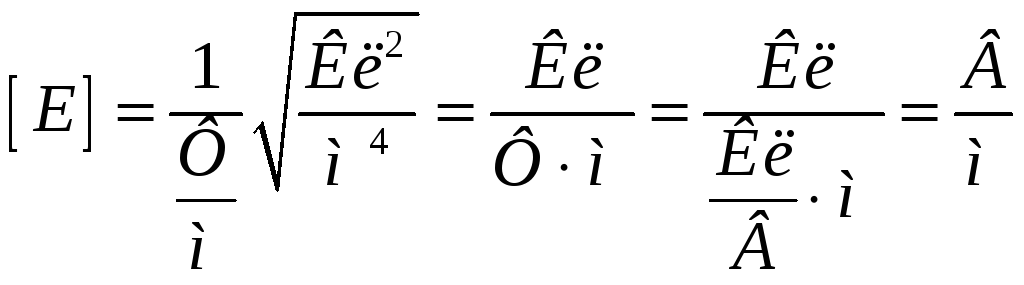
Проводим расчет:
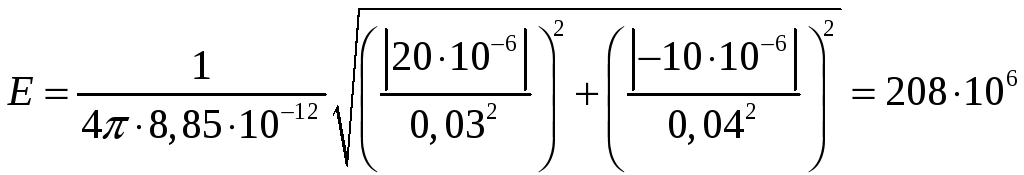 В/м=208
МВ/м
В/м=208
МВ/м
![]() Ответ:
Ответ:
![]() 208
МВ/м
208
МВ/м
Задача № 319
На
бесконечном тонкостенном цилиндре
диаметром
![]() см
равномерно распределен заряд с
поверхностной плотностью
см
равномерно распределен заряд с
поверхностной плотностью
![]() мкКл/м2.
Определить напряженность поля в точке,
отстоящей от поверхности цилиндра на
мкКл/м2.
Определить напряженность поля в точке,
отстоящей от поверхности цилиндра на
![]() см.
см.
|
Дано:
|
Решение. Напряженность поля, создаваемого бесконечно длинным равномерно заряженным цилиндром равна:
|
|
Найти:
|
![]() -
линейная плотность заряда;
-
линейная плотность заряда;
![]() -
расстояние от оси цилиндра.
-
расстояние от оси цилиндра.
Выразим
линейную плотность
![]() через поверхностную плотность
через поверхностную плотность![]() .
Для этого выделим элемент цилиндра
длиной
.
Для этого выделим элемент цилиндра
длиной
![]() и выразим находящийся на нем заряд
и выразим находящийся на нем заряд
![]() двумя способами:
двумя способами:
![]()
![]() -
радиус цилиндра.
-
радиус цилиндра.
![]()
![]()
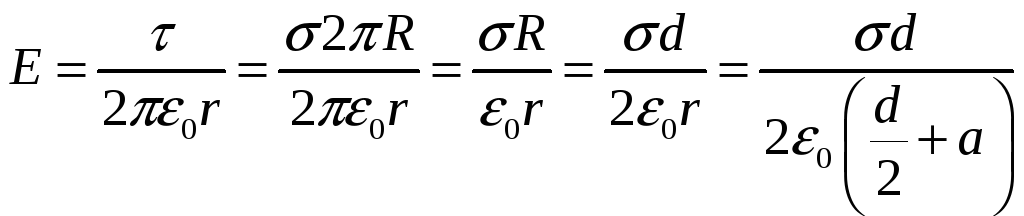
Проводим анализ размерности:
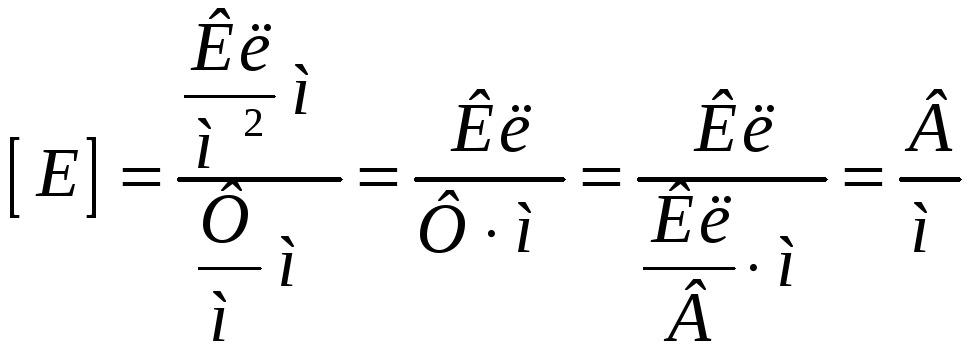
Проводим расчет:
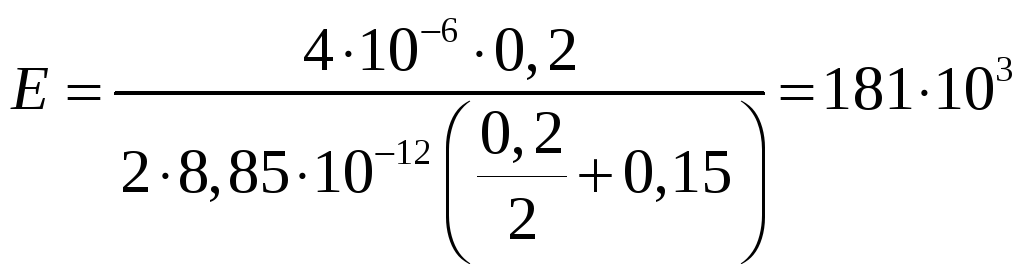 В/м=181кВ/м
В/м=181кВ/м
Ответ:
![]() 181кВ/м
181кВ/м
Задача № 328
Четыре
одинаковых капли ртути, заряженных до
потенциала
![]() ,
сливаются в одну. Каков потенциал
,
сливаются в одну. Каков потенциал
![]() образовавшейся капли?
образовавшейся капли?
|
Дано:
|
Решение.
Пусть
Заряд, который имеет каждая капля равен:
|
|
Найти:
|
При слиянии капель заряд образующейся капли равен:
![]()
Определяем радиус образующейся капли. Объем первоначальной капли:
![]()
Объем объединенной капли:
![]()
Радиус объединенной капли:
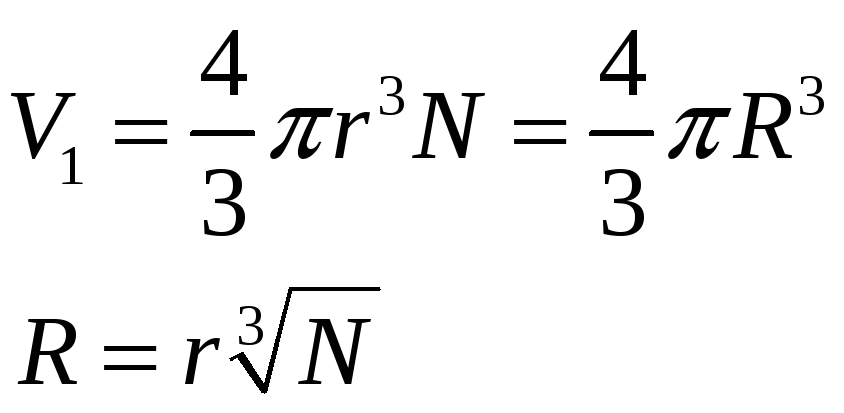
Емкость объединенной капли:
![]()
Потенциал объединенной капли:
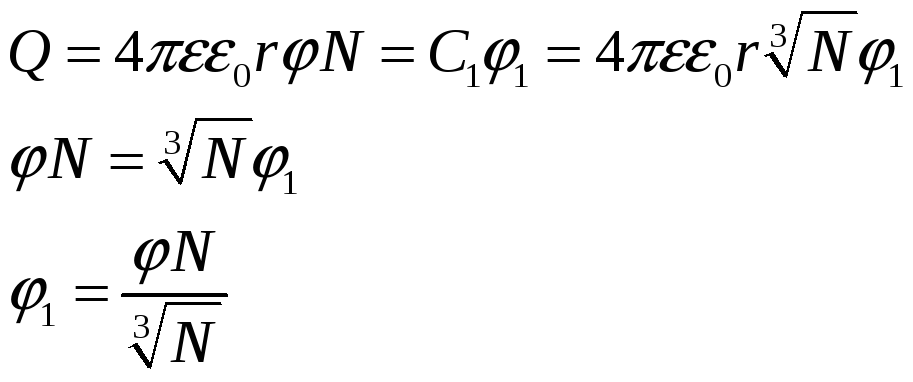
Проводим расчет:
![]()
Ответ:
![]()
Задача № 340
При
бомбардировке неподвижного ядра калия
![]() -частицей
сила отталкивания между ними достигла
-частицей
сила отталкивания между ними достигла
![]() .
На какое наименьшее расстояние
приблизилась
.
На какое наименьшее расстояние
приблизилась
![]() -частица
к ядру атома калия? Какую скорость имела
-частица
к ядру атома калия? Какую скорость имела
![]() -частица
вдали от ядра?. Влиянием электронной
оболочки пренебречь.
-частица
вдали от ядра?. Влиянием электронной
оболочки пренебречь.
|
Дано:
1
а.е.м.=
|
Решение.
Ядро
атома калия
|
|
Найти:
|
Определяем расстояние:
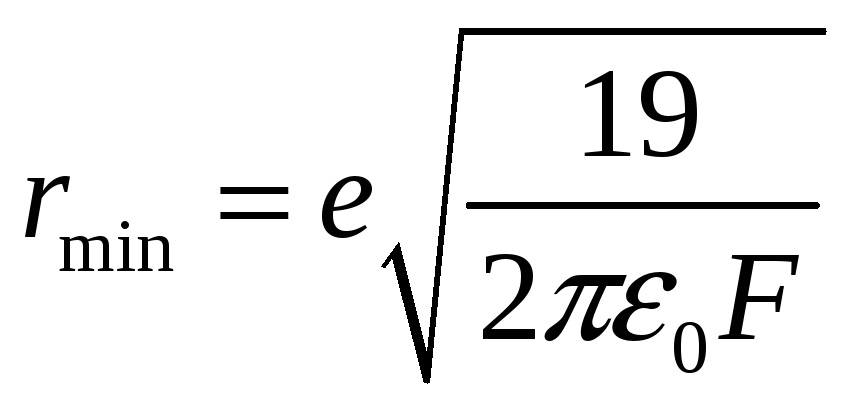
Потенциальная
энергия взаимодействия ядра калия с
![]() -частицей
на таком расстоянии равна:
-частицей
на таком расстоянии равна:
![]()
Из
закона сохранения энергии определяем
скорость
![]() -частицы
вдали от ядра:
-частицы
вдали от ядра:
![]() масса
масса
![]() -частицы;
-частицы;
![]() а.е.м.
а.е.м.
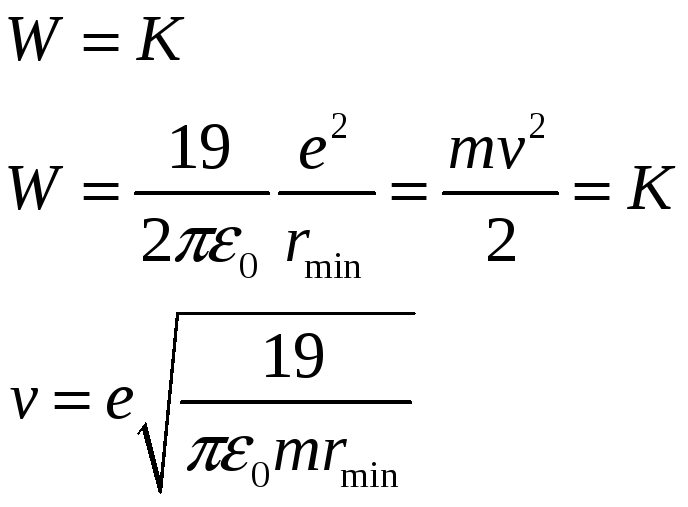
Анализ размерности:
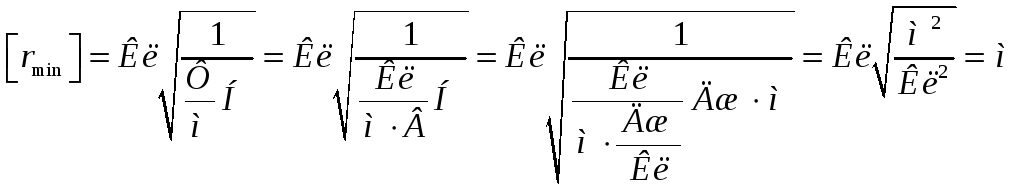
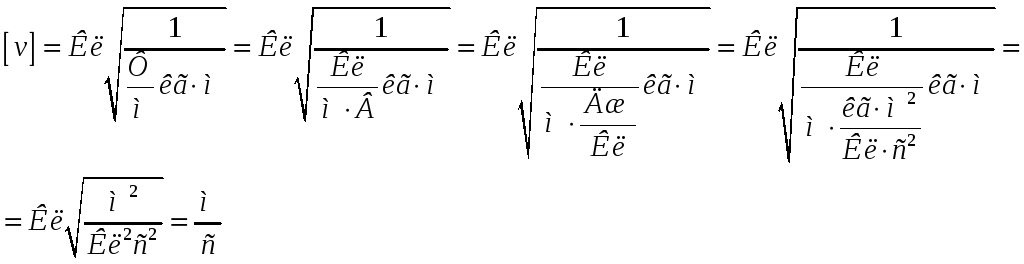
Поводим расчет:
![]() м=9,35фм
м=9,35фм
![]() м/с=16,8Мм/с
м/с=16,8Мм/с
Ответ:
![]() 9,35фм
9,35фм
![]() 16,8Мм/с
16,8Мм/с
Задача № 401
Проволочный
виток радиусом
![]() см
расположен в плоскости магнитного
меридиана. В центре установлена небольшая
магнитная стрелка, могущая вращаться
вокруг вертикальной оси. На какой угол
отклонится стрелка, если по витку пустить
ток силой
см
расположен в плоскости магнитного
меридиана. В центре установлена небольшая
магнитная стрелка, могущая вращаться
вокруг вертикальной оси. На какой угол
отклонится стрелка, если по витку пустить
ток силой
![]() .
Горизонтальную составляющую индукции
земного магнитного поля принять равной
.
Горизонтальную составляющую индукции
земного магнитного поля принять равной
![]() мкТл
мкТл
|
Дано:
|
Решение.
|
|
Найти:
|
В
отсутствие тока в витке магнитная
стрелка устанавливается в плоскости
магнитного меридиана вдоль оси
![]() .
При пропускании тока по витку в точке
возникает магнитное поле, вектор индукции
которого направлен вдоль оси
.
При пропускании тока по витку в точке
возникает магнитное поле, вектор индукции
которого направлен вдоль оси
![]() и
равный по величине:
и
равный по величине:
![]()
где
![]() - радиус витка,
- радиус витка,
![]() -
магнитная проницаемость среды (для
воздуха
-
магнитная проницаемость среды (для
воздуха
![]() ),
),
![]()
![]() -
магнитная постоянная,
-
магнитная постоянная,
![]() -
сила тока в витке. В этом случае магнитная
стрелка повернется на некоторый угол
в направлении равнодействующей индукции
двух полей. Значит:
-
сила тока в витке. В этом случае магнитная
стрелка повернется на некоторый угол
в направлении равнодействующей индукции
двух полей. Значит:
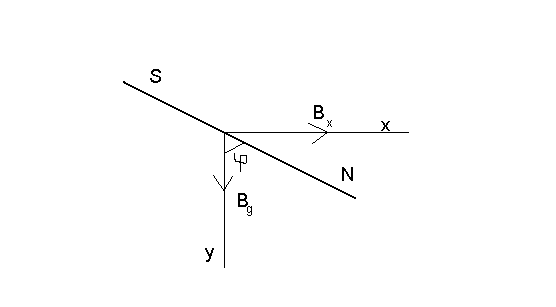
![]()
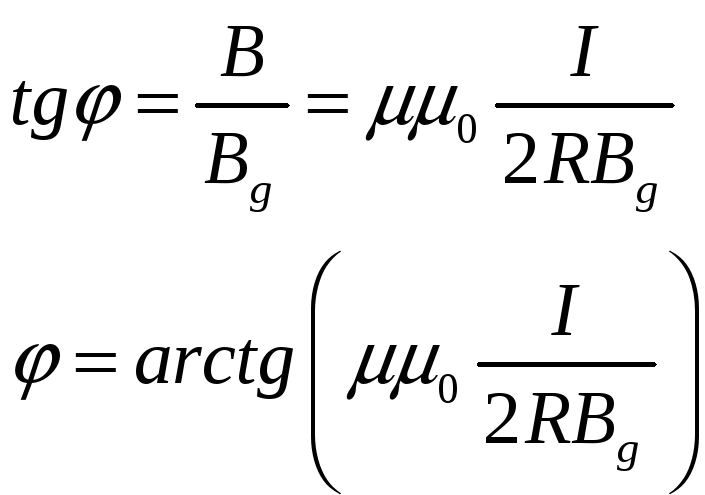
Размерность:
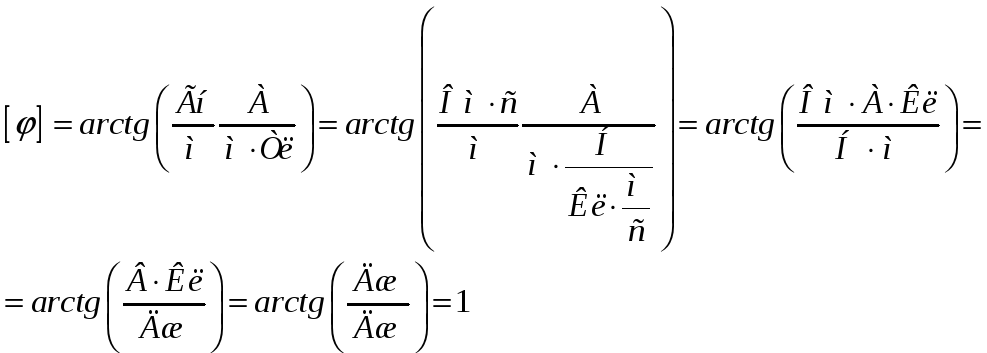
Проводим расчет:
![]()
Ответ:
![]()
Задача № 416
Виток
радиусом
![]() см,
по которому течет ток силой
см,
по которому течет ток силой![]() ,
свободно установился в однородном
магнитном поле напряженностью
,
свободно установился в однородном
магнитном поле напряженностью
![]() А/м.
виток повернули относительно диаметра
на угол
А/м.
виток повернули относительно диаметра
на угол
![]() .
Определить совершенную работу.
.
Определить совершенную работу.
|
Дано:
|
Решение.
|
|
Найти:
|
При медленном повороте контура в магнитном поле индукционными токами можно пренебречь и считать ток в контуре неизменным. Работа сил поля в этом случае определяется выражением:
![]()
Где
![]() и
и
![]() —
магнитные потоки, пронизывающие контур
в начальном и конечном положениях.
—
магнитные потоки, пронизывающие контур
в начальном и конечном положениях.
Работа внешних сил будет равна модулю работе сил поля и противоположна ей по знаку, т. е.:
![]()
Так
как в начальном положении контур
установился свободно (положение
устойчивого равновесия), то момент
внешних сил, действующий на контур,
равен нулю. В этом положении вектор
магнитного момента
![]() контура
сонаправлен с вектором
контура
сонаправлен с вектором
![]() и
магнитный поток
и
магнитный поток
![]() максимален
(
максимален
(![]() ),
т. е.
),
т. е.
![]() (где
S
— площадь контура). В конечном положении:
(где
S
— площадь контура). В конечном положении:
![]()
Значит:
![]()
![]()
![]()
Проверка размерности:
![]()
Проводим расчет:
![]()
Ответ:
![]()
Задача № 452
В
однородном магнитном поле с индукцией
![]() Тл
вращается с частотой
Тл
вращается с частотой
![]() стержень длиной
стержень длиной
![]() см. Ось вращения параллельна линиям
индукции и проходит через один из концов
стержня, перпендикулярно его оси.
Определить разность потенциалов
см. Ось вращения параллельна линиям
индукции и проходит через один из концов
стержня, перпендикулярно его оси.
Определить разность потенциалов
![]() на
концах стержня.
на
концах стержня.
|
Дано:
|
Решение. Согласно закону Фарадея:
где изменение магнитного потока:
Так
как
|
|
Найти:
|
За
один оборот стержень пересекает площадь
![]() за время
за время
![]() .
.
![]() -
период обращения.
-
период обращения.
Значит:
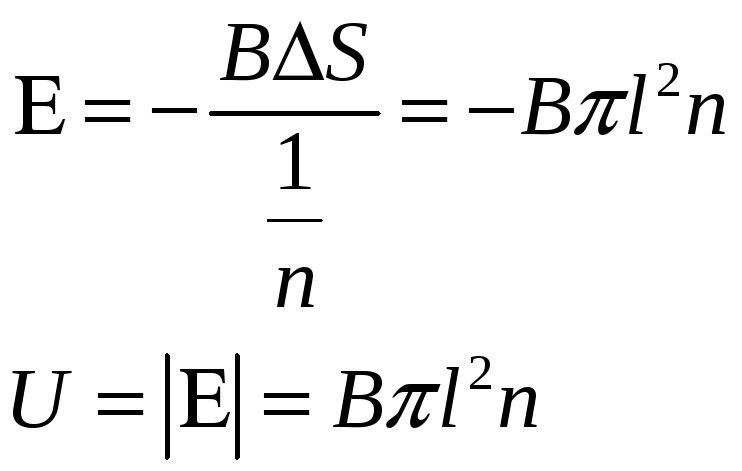
Размерность:
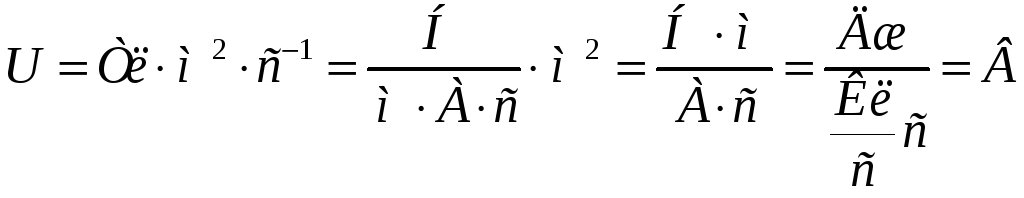
Проводим расчет:
![]()
Ответ:
![]()
Задача № 466
Соленоид
содержит
![]() витков. Сечение сердечника (из немагнитного
материала)
витков. Сечение сердечника (из немагнитного
материала)
![]() см2.
По обмотке течет ток, создающий поле с
индукцией
см2.
По обмотке течет ток, создающий поле с
индукцией
![]() мТл.
Определить среднее значение Э.Д.С.
мТл.
Определить среднее значение Э.Д.С.
![]() самоиндукции, которая возникает на
зажимах соленоида, если ток уменьшается
практически до нуля за время
самоиндукции, которая возникает на
зажимах соленоида, если ток уменьшается
практически до нуля за время
![]() мс.
мс.
|
Дано:
|
Решение. Индуктивность соленоида равна:
Индукция поля на оси соленоида равна:
|
|
Найти:
|
Сила тока в соленоиде:
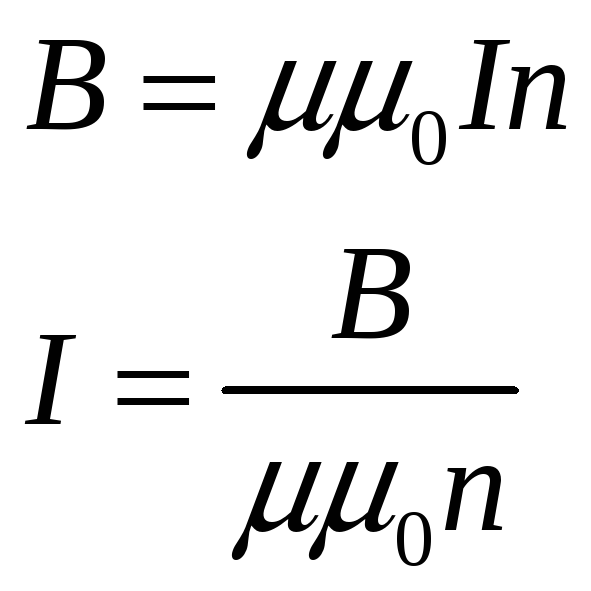
При протекании тока через соленоид в соответствии с законом электромагнитной индукции на его зажимах возникает ЭДС самоиндукции, равная:
![]()
![]()
Так как сила тока падает практически до нуля, то:
![]()

Размерность:

Проводим расчет:
![]()
Ответ:
![]()
Литература
-
Савельев И.В. Курс общей физики. М.: Наука, 1985‑1987.
-
Волькенштейн В.С. Сборник задач по общему курсу физики. М.: Наука, 1986.
-
Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 2000.
-
Беликов Б.С. Решение задач по физике. М.: Высшая школа, 1986.