Решение

Физическая система состоит из двух тел: лодки с охотником массы m₁ и пули массой m₂.

В первом состоянии (до выстрела) импульс системы относительно воды был равен

= (m₁ +m₂) ∙ , (1),

где - скорость относительно воды лодки с охотником и пули до выстрела (рис. 1)

рис. 1

рис. 2

Во втором состоянии (после выстрела) импульс системы относительно воды стал равным

= m₁ + m₂ (2),

где - скорость относительно воды лодки с охотником после выстрела;

- скорость относительно воды пули после выстрела (рис. 2).

Согласно закону сложения скоростей скорость пули относительно воды равна геометрической сумме скорости пули относительно лодки и скорости лодки относительно воды (рис. 3)

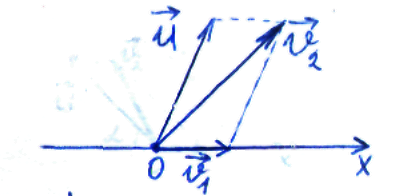
рис. 3

₌ + (3)

Подставив выражение (3) в уравнение (2), получаем:

= m₁ + m₂( + ) = m₁ + m₂ + m₂ (4)

Система «лодка + пуля» незамкнута, но сумма проекций всех внешних сил (сил тяжести и силы реакции опоры), действующих на эту систему, на ось ох (рис. 2) равна 0, а сила трения пренебрежимо мала, следовательно, проекция импульса данной системы на ось ох сохраняется:

р_1х = р_2х, (5),

где р_1х - проекция на ось ох импульса системы до выстрела,

р_2х - проекция на ось ох импульса системы после выстрела.

Спроектировав выражения (1) и (4) на ось ох, получим

р_1х -= (m₁ +m₂) ∙ (6)

р_2х = m₁ + m₂Ucos + m₂ (7)

Уравнения (6) и (7) подставим в (5):

(m₁ +m₂) ∙ = m₁ + m₂Ucos + m₂

Выражая скорость лодки после выстрела, получим:

= ((m₁ +m₂) ∙ - m₂Ucos) / (m₁ +m₂).

Расчеты:

= ((110+20∙10^-3)∙2 - 20∙10^-3∙600 cos 30⁰) / (110+20∙10^-3) = 1,9 (м/с).

Ответ: 1,9 м/с Правильно

Задача 136

В центре скамьи Жуковского массой 10 кг и радиусом 2 м, вращающейся с угловой скоростью 1,5 рад/с, стоит человек и держит на вытянутых руках две гири по 1 кг каждая. Расстояние от каждой гири до оси вращения составляет 80 см. С какой угловой скоростью начнет вращаться скамья, если человек сожмет руки так, что гири окажутся на оси вращения? Считать, что момент инерции человека относительно оси вращения пренебрежимо мал.

Дано:

m_с = 10 кг

R = 2 м

= 1,5 рад/с

m_г1 = m_г2 = m_г = 1 кг

r₁ = 80 см = 0,8 м (СИ)

r₂ = 0

Найти:

Решение

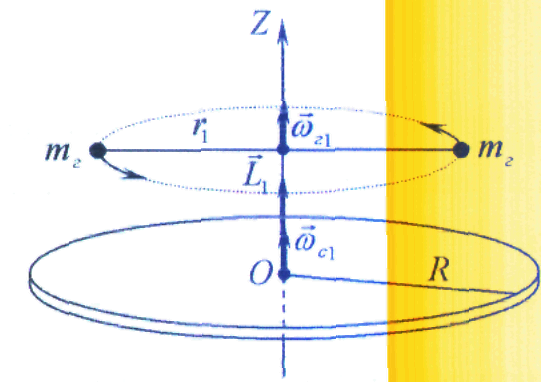
Скамья Жуковского представляет собой однородный диск, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через центр диска перпендикулярно его плоскости. Момент инерции скамьи относительно этой оси равен

I_c = (1)

Физическая система состоит из скамьи с человеком и двух гирь.

По условию момент инерции человека относительно оси вращения равен нулю, т.е. I_ч= 0. Гири можно считать материальными точками и, т.к. они находятся на одном и том же расстоянии r до оси вращения, то момент инерции гирь относительно этой оси равен

I_г = m_г1 r² +m_г2 r² = 2m_г r² (2),

где r – расстояние от каждой гири до оси вращения. Поскольку момент инерции I всей системы относительно оси вращения равен сумме моментов инерции всех тел системы относительно этой же оси, с учетом (1) и (2) имеем

I = I_c + I_г = + 2m_г r² =

Момент инерции системы относительно оси вращения в первом состоянии (каждая гиря находится на расстоянии r₁ от оси) равен

I₁= + 2m_г r₁² =

Так как в первом случае скамья и гири вращаются относительно оси с одинаковой угловой скоростью = = , ^{тогда момент импульса системы относительно оси Oz будет равен}

L_1z = I₁ = ∙ (3)

Во втором состоянии (каждая гиря находится на расстоянии r₂ от оси вращения) момент инерции системы относительно оси вращения равен

I₂ = + 2m_г r₂² = ,

^{а поскольку скамья и гири вращаются относительно оси с одинаковой угловой скоростью} = = , тогда момент импульса L_2z системы относительно оси Oz будет равен:

L_2z = I₂ = ∙ (4).

Так как моменты внешних сил (сил тяжести и реакции опоры), действующих на систему относительно оси вращения Oz, равны нулю, то момент импульса системы относительно этой оси сохраняется:

L_1z = L_2z (5)

^{Подставим в (5) выражения (3) и (4):}

∙ = ∙_,

откуда угловая скорость выражается как

^{Подставляя числовые значения, вычислим угловую скорость} :

= 1,5 ∙ = 1,6 (рад/с)

Ответ: 1,6 рад/с Правильно