20

Белорусский государственный университет

информатики и радиоэлектроники

Кафедра физики

Контрольная работа №1, 2 по физике

вариант 6

выполнил: студент 1 курса ФНиДО, ИИ,

Проверила: Дорошевич Ирина Леонидовна

Минск 2010

Задача 106

Частица движется так, что ее скорость изменяется со временем по закону   (м/с), где t – время в секундах. В начальный момент времени t₀= 0 частица находилась в точке с координатами (1 м; 0; 0). Найти: 1) зависимость от времени модуля скорости частицы; 2) зависимости от времени вектора ускорения и модуля ускорения; 3) кинематический закон движения частицы; 4) радиус-вектор в момент времени t₁=1,0 c; 5) модуль перемещения частицы за время .

Дано:

, м/с

t₀ = 0

t₁ = 1

∆t = t₁- t₀

Найти: , , , , ∆

Решение

^{Физическая система состоит из одной частицы, скорость которой изменяется со временем по закону}

, (м/с).

Так как вектор скорости частицы связан с его проекциями на координатные оси

,

^{то зависимости от времени проекции вектора скорости данной частицы на координатные оси имеют вид}

= 4t, м/с

= 3, м/с

(t)= -t², м/с

Модуль скорости частицы связан с его проекциями на координатные оси как

, тогда искомая зависимость модуля скорости частицы от времени имеет вид

, м/с

1. Вектор ускорения можно выразить через его проекции

на координатные оси следующим образом

^{Из определения вектора ускорения}

^{следует, что проекции вектора ускорения частицы на координатные оси равны производным одноименных проекций ее скорости по времени:}

^,,

^{Учитывая, что}

= 4t, м/с

= 3, м/с

(t)= -t², м/с

найдем проекции вектора ускорения частицы на координатные оси:

^{= 4 м/с2}

^{= 0}

^{= -2t м/с2}

Тогда зависимость от времени вектора ускорения частицы имеет вид

^{, м/с2}

Модуль ускорения связан с его проекциями на координатные оси как

тогда модуль ускорения частицы зависит от времени:

, м/с²

2. ^{Кинематический закон движения частицы - это зависимость от времени ее радиуса-вектора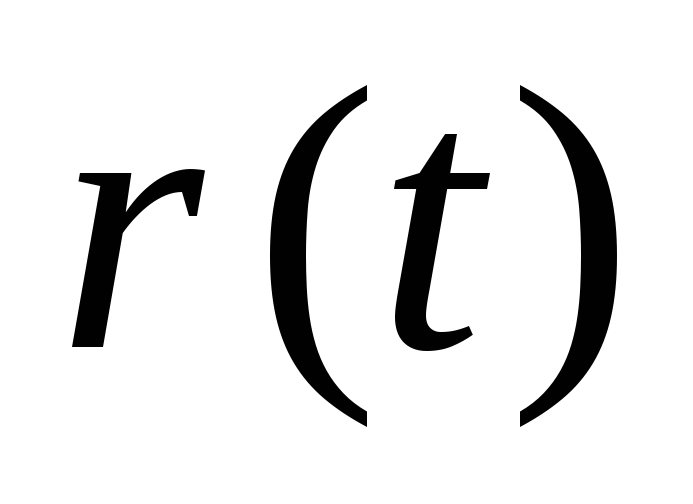} . Так как радиус-вектор движущейся частицы можно выразить через ее координаты (проекции радиуса-вектора на координатные оси) как

то для ответа на вопрос задачи необходимо найти зависимости от времени координат

частицы.

Из определения вектора скорости

следует, что проекции вектора скорости частицы на координатные оси равны ^{производным ее одноименных координат по времени:}

Так как

= 4t, м/с и , то получаем, что =4t

^{Умножив левую и правую часть этого уравнения на dt, имеем dx=4tdt.}

Полученное уравнение является дифференциальным уравнением с разделенными переменными, решение которого получают интегрированием левой и правой части равенства:

dx=4tdt

x = 4; x=2t²+c₁

Поскольку интегралы неопределенные, то полученное выражение содержит константу С₁ значение которой найдем из начальных условий:

x₀=2t₀ ²+c₁

подставляя значения Х_о = 1 м и t_о ⁼ 0, получаем С₁= 1 м. Тогда зависимость от времени координаты x(t) частицы имеет вид

x(t)=2t²+1, м

Аналогично найдем зависимость от времени y(t) и z(t).

Так как

и = 3, то =3;

=3t+C₂

Так как при t₀=0, координата y₀=0, то С₂=0

Тогда зависимость от времени координаты y(t) частицы имеет вид y(t) = 3t.

Так как

и (t)= -t² , м/с² , то

z = -

Так как при t₀=0, координата z₀=0, то С₃=0

Тогда зависимость от времени координаты z(t) частицы имеет вид

z (t) = - (м)

^{Определив зависимости от времени координат частицы, x(t), y(t),} z(t), запишем ^{кинематический закон ее движения:}

, (м)

^{Для нахождения радиус-вектора частицы в определенный момент времени t}₁ ^{подставим} в кинематический закон движения частицы значение ^t₁^{=1,0 с:}

, (м)

Проведя вычисления, получаем:

, (м)

По определению вектор перемещения ∆ частицы за время ∆t = t₁- t₀ равен

∆ = (t₁) - (t₀)

Так как, , то с учетом начальных условий

x₀ =1 м, y₀ = z₀ = 0 радиус-вектор частицы момент времени равен =1(м). Тогда вектор перемещения составляет

, м

а его модуль равен

(м)

^Ответ: , м/с Правильно

4, м/с²

, м/с²

^{, м}

^,(м)

^{∆= 3,62 м}