Итерационная процедура отыскания главного характеристического корня.

Приведем метод отыскания наибольшего характеристического корня матрицы не решая при этом характеристического уравнения. Он позволяет определить значение наибольшего характеристического корня в тех случаях, когда он существует.

Предположим, что главный вещественный корень существует. Представим матрицу А в виде , где

- матрица, составленная из собственных векторов матрицы А,

- диагональная матрица, с диагональными элементами, стоящими на диагонали.

- матрица, обратная матрице U.

(представление является прямым следствием определения собственного вектора как ненулевого решения уравнения с ).

Предположим, что главный корень – это , причем при достаточно больших k настолько больше любого из значений , что последние можно считать нулями. Тогда можно записать следующее:

Умножив обе части этого выражения справа на ненулевой вектор-столбец х, находим:

, где .

Введем вектор 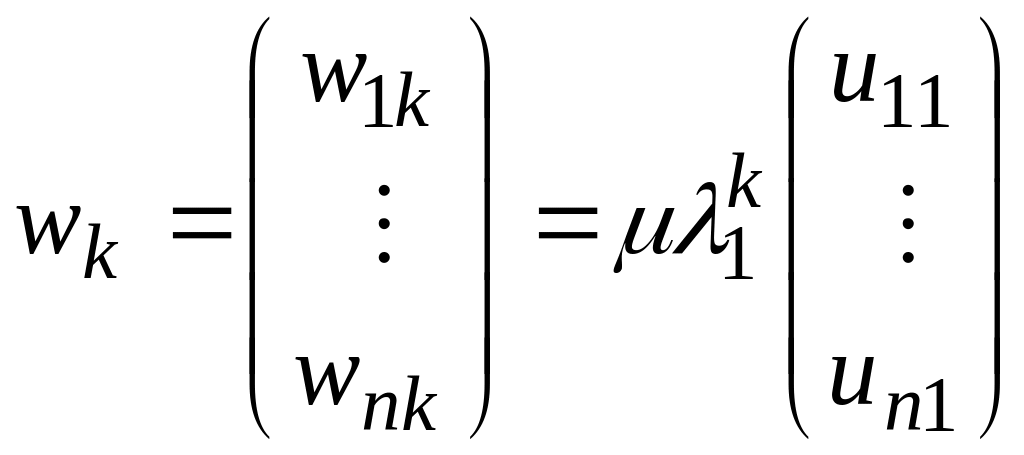. В таком случае , аналогично имеем . Из определения следует, что . Таким образом, произведение, полученное в результате повторных умножений матрицы А на вектор х, равно такому вектору , у которого отношение каждого элемента к соответствующему элементу представляет одну и ту же величину. Она как раз и является приближенным значением наибольшего характеристического корня. По мере увеличения величины k точность аппроксимации растет, так что продолжая этот процесс, можно вычислить значение наибольшего характеристического корня с любой требуемой точностью.

Пример 4. Дана матрица . Найти наибольший характеристический корень приближенным способом.

Решение. Пусть . Возьмем произвольный вектор . Вычислим последовательно

Легко можно увидеть что отношение координат векторов при возрастании k стремится к 3. Значит главный характеристический корень будет равен 3.(Очевидно, что можно сравнивать не координаты векторов , а их длины. Результат будет тот же. Сравнение длин тем удобнее, чем больше координат имеют вектора ) Кроме того, наблюдая за последовательными изменениями величины вектора , можно прийти к следующему заключению: по мере того как k увеличивается, отношение между элементами этого вектора приближается к пропорции 1: 2. Таким образом, характеристический вектор, соответствующий главному характеристическому корню 3, равен