Задача 3.

Вычислить среднюю тарифную заработную плату работников и коэффициент вариации по следующим данным:

Заработная плата, млн р.	14–15	15–16	16–17	17–18	18–19	Всего
Число работников	8	15	10	7	3	43

Решение.

_{Средняя тарифная заработная плата работников}

_{где xi – середина i-го интервала; ni - частота i-го интервала.}

Средняя тарифная заработная плата работников

Среднеквадратичное отклонение

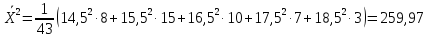
среднеквадратичное отклонение

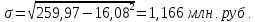
коэффициент вариации

Вывод:так как коэффициент вариации меньше 30%, то среднее может служить характеристикой совокупности

Задача 4.

По данным задачи 3: 1) определите моду и медиану изучаемого показателя; 2) постройте гистограмму; 3) оцените характер асимметрии.

Решение.

1) мода – варианта с наибольшей частотой

в качестве модального интервала выбираем интервал с наибольшей частотой – им является интервал 15–16

где- начало (нижняя граница) модального интервала;- величина интервала;- частота модального интервала;- частота интервала, предшествующего модальному;- частота интервала, следующего за модальным.

Таким образом, мода равна:

_{Медиана – варианта, которая делит вариационный ряд пополам}

Расчет медианы для интервального ряда производится по формуле:

– начало (нижняя граница) медианного интервала; i_Me – величина интервала; – сумма всех частот ряда;– сумма накопленных частот вариантов до медианного;– частота медианного интервала.

Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот

Заработная плата, млн р.	14–15	15–16	16–17	17–18	18–19
накопленые частоты	8	23	33	40	43

_{Медианным интервалом является интервал 15-16}

Медиана равна:

млн. руб.

2) график интервального ряда распределения (гистограмма)

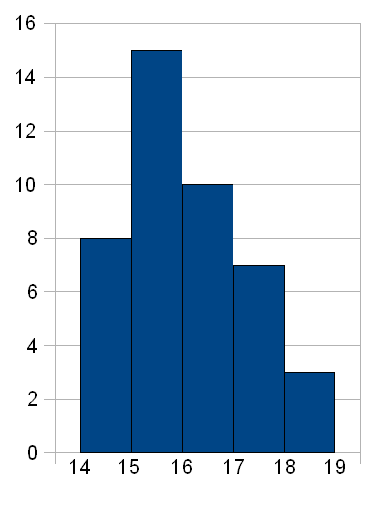
3) Высчитаем коэффициент асимметрии:

Так как 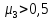, то асимметрия значительная правосторонняя.

Задача 5.

На основе данных о динамике междугородных разговоров определить: 1) среднегодовое количество междугородных разговоров за весь период; 2) ежегодные абсолютные приросты междугородных разговоров и среднегодовой прирост за весь период; 3) цепные и базисные темпы роста междугородных разговоров; 4) среднегодовой темп роста за весь период.

Проанализируйте полученные показатели. Напишите вывод о характере изменения количества междугородных разговоров по годам.

Исходные данные: 1-й год – 190,2 тыс.; 2-й год – 210,4 тыс.; 3-й год – 229,8 тыс.; 4-й год – 245,4 тыс.; 5-й год – 270,0 тыс. междугородных телефонных разговоров.

Решение.

Абсолютный прирост, показывает на сколько единиц изменился данный уровень по сравнению с первым (базисный уровень) или предшествующим (цепной прирост).

_{базисный}

где – объем продукции вi-ом периоде.

_цепной

Темп роста показывает, во сколько раз изменился данный уровень по сравнению с первым(базисный темп роста) или предшествующим (цепной) _{базисный}

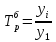
цепной

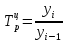
Темп прироста показывает, на сколько процентов изменился данный уровень по сравнению с первым (базисный темп прироста) или предшествующим (цепной темп прироста).

_{базисный}

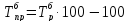
_цепной

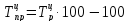
_{Составим сводную таблицу рассчитанных показателей}

		Абсолютный прирост			Темп роста			Темп прироста
Год	Количество, Yi, тыс.	Базисный, Δyб, тыс.	Цепной, Δyц, тыс.	Базисный, Трб		Цепной, Трц	Базисный, Тпрб, %		Цепной, Тпрц, %
1	190,2
2	210,4	20,2	20,2	1,106		1,106	10,620		10,620
3	229,8	39,6	19,4	1,208		1,092	20,820		9,221
4	245,4	55,2	15,6	1,290		1,068	29,022		6,789
5	270	79,8	24,6	1,420		1,100	41,956		10,024

_{Среднегодовой объем международных разговоров}

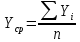
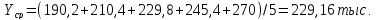
_{Среднегодовой абсолютный прирост}

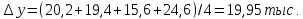
_{Среднегодовой темп роста}

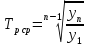
_{Среднегодовой темп прироста}

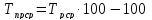
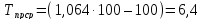
Вывод:За 5 лет объем международных звонков вырос со 190,2 до 270тыс, что оставляет 42%. Средний рост составил 19,95тыс. в год или 6,4%. Самый наибольший рост был зафиксирован в 5-м году – 24,6 тыс.