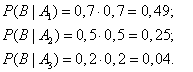5 ВАРИАНТ
|Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
--------------------------------------------------------------
|Номер варианта | 8 | 11 | 3 | 21 | 29 | 17 | 26 | 12 |
--------------------------------------------------------------
1. На десяти карточках написаны буквы А, А, А, М, М, Т, Т, Е, И, К. После перестановки вынимают наугад одну карточку за другой и раскладывают их в том порядке, в каком они были вынуты. Найти вероятность того, что на карточках будет написано слово “математика”.
Р(А)=m/n n=10! m=2!*2!*3!
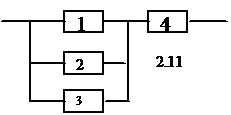
2. Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4 соответственно равны p1=0,1; p2=0,2; p3=0,3; p4=0,4; p5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.
Дано:
p1=0,1; p2=0,2; p3=0,3; p4=0,4; p5=0,5.
А - сигнал пройдет со входа на выход.
р(А) - ?
Решение.
р(
)
= 1 – 0,1 = 0,9;
р(
)
= 1 – 0,4 = 0,6
р(
∙
)
= 0,9 * 0,6 = 0,54 – вероятность того, что сигнал
пройдет по первой цепи;
р(
)
= 1 – 0,2 = 0,8; – вероятность того, что сигнал
пройдет по второй цепи;
р(
)
= 1 – 0,3 = 0,7 – вероятность того, что сигнал
пройдет по третьей цепи;
р(А) = р(
∙
)
+ р(
)
+ р(
)
= 0,54 + 0,8 + 0,7 = 2,04.
Ответ: р(А) = 2,04.
|
3. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком. Решение. Возможны три гипотезы:
Так как вызов на линию огня любого
стрелка равновозможен, то
В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
по формуле Байеса находим вероятность
гипотезы
|
-
на линию огня вызван первый стрелок,
-
на линию огня вызван второй стрелок,
-
на линию огня вызван третий стрелок.
после
опыта:
4. Монету подбрасывают восемь раз. Какова вероятность того, что она четыре раза упадет гербом вверх?
Рассмотрим задачу: монету подбрасывают
200 раз. Необходимо вычислить вероятность
появления герба в 90 испытаниях. Применим
формулу Бернулли(
):
.
5. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
-
Вариант
x1
X2
x3
x4
x5
p1
p2
p3
p4
p5
5.29
1
4
5
7
8
0,3
0,3
0,1
0,15
0,15
Решение.
Математическое ожидание равно сумме произведений всех возможных значений X на их вероятности:
М (X) = 1 ∙ 0,3 + 4 ∙ 0,3∙+ 5 ∙ 0,1 + 7 ∙ 0,15 + 8 ∙ 0,15 = 0, 3 + 1,2 + 0,5 + 1,05 + 1,2 = 3,75.
Для вычисления дисперсии воспользуемся формулой:
D(X) =
-
М (X) = 3,75;
Напишем закон распределения
:
-
Вариант
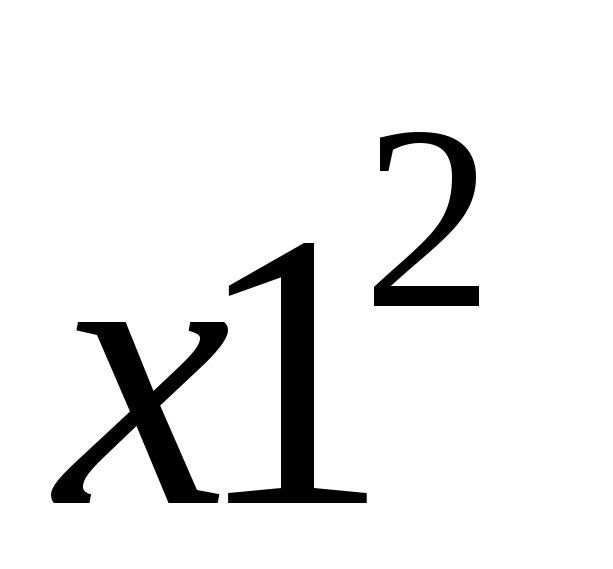
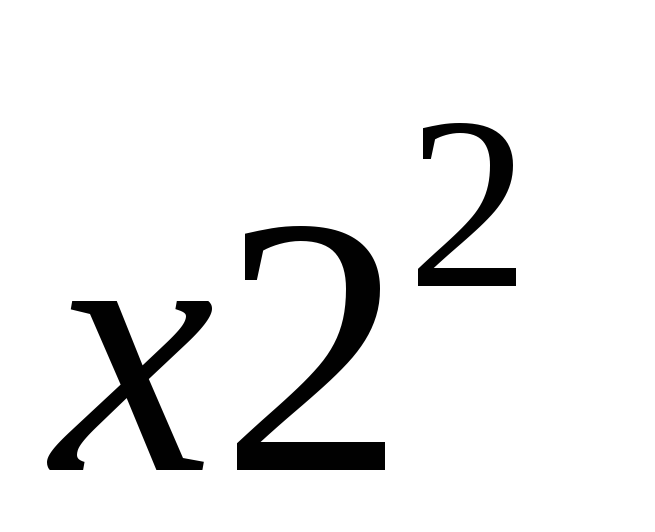
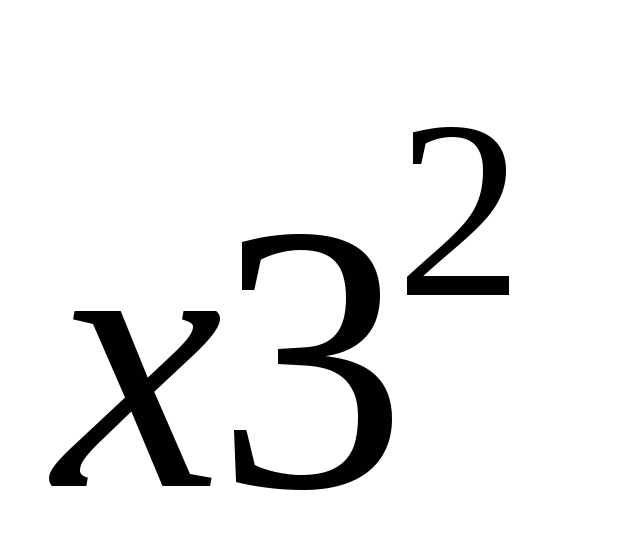
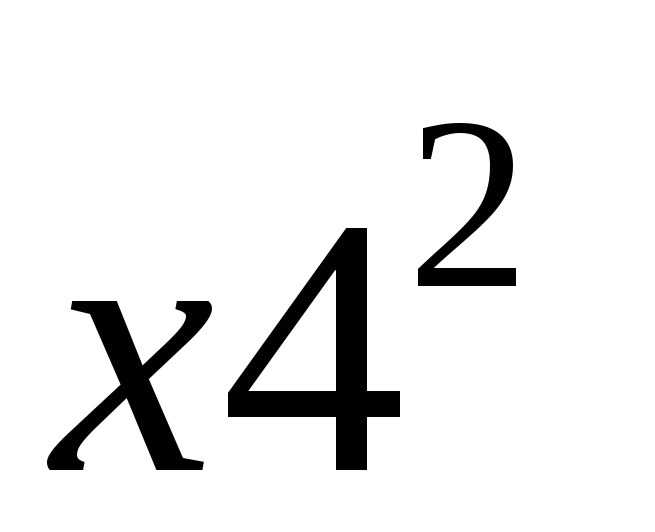
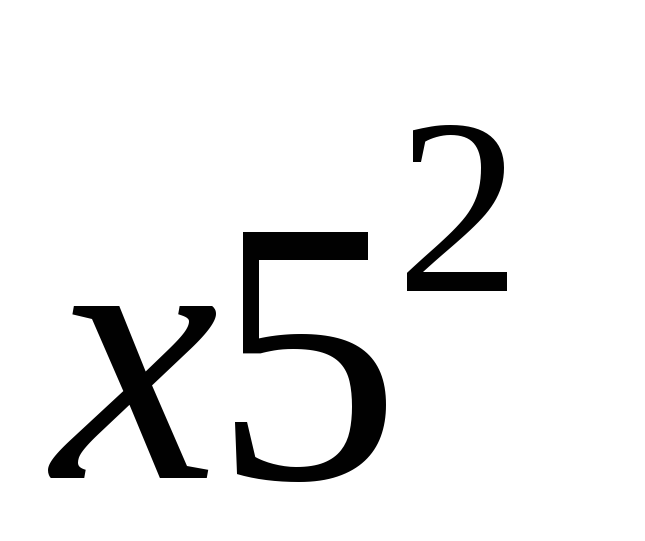
p1
p2
p3
p4
p5
5.29
1
16
25
49
64
0,3
0,3
0,1
0,15
0,15
Найдем математическое ожидание
:
= 1 ∙ 0,3 + 16 ∙
0,3 + 25 ∙ 0,1 + 49 ∙
0,15 + 64 ∙ 0,15 = 0,3 + 4,8 + 2,5 + 7,35
+ 9,6 = 24,55.
Найдем искомую дисперсию:
D(X)
=
-
=
24,55
-
=
10,
49.
Ответ: М (X) = 3,75; D(X) = 10,49.
|Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
--------------------------------------------------------------
|Номер варианта| 8 | 11 | 3 | 21 | 29 | 17 | 26 | 12 |
6. Случайная величина х задана плотностью вероятности
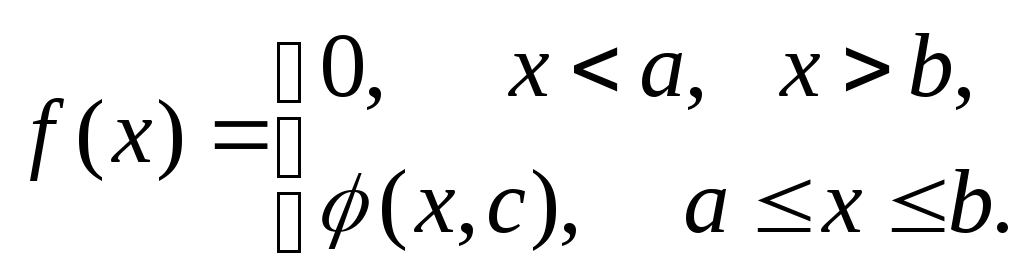
Определить константу С, математическое
ожидание, дисперсию, функцию распределения
величины Х, а также вероятность ее
попадания в интервал
.
-
Вариант
x,c)a
b
6.17
c x5
0
1
0,5
0,7
Решение.
Константу с вычислим исходя из условия нормировки:
,
откуда с = 6.
Так как плотность вероятности задана различными формулами на разных интервалах, то и функцию распределения будем искать для каждого интервала в отдельности.
Для
x
< 0
,
для
0£x£1
,
для
x
>
1
.
Окончательно имеем
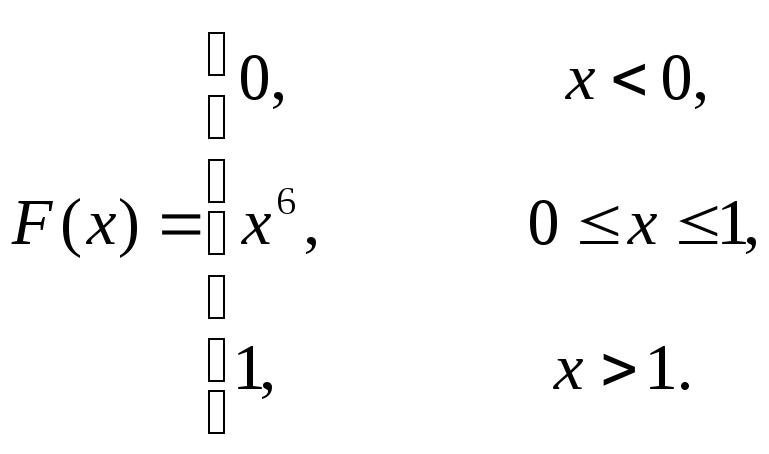
Вероятность
P{0,5
x
0,7}=
.
В задачах 7.1-7.30 (условия приведены в табл. 1.3) случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).
Таблица 1.3
-
Вариант
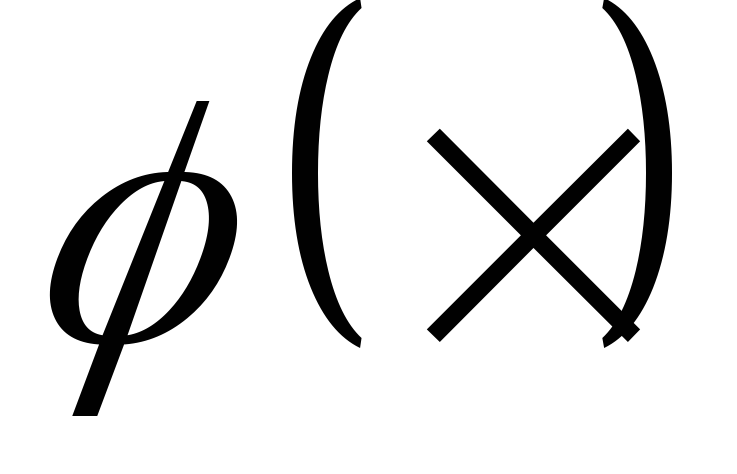
a
b
7.26
0
1,5
0,5
Так как Х равномерно распределена в интервале 0, 1,5, то ее плотность вероятности равна:
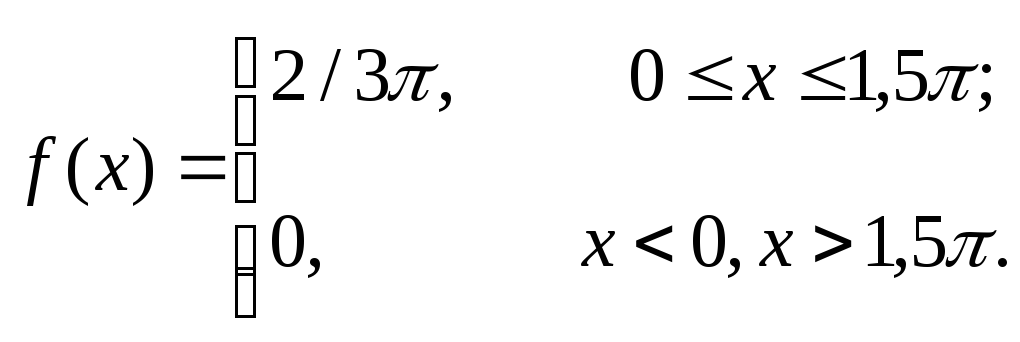
Построим график величины Y =
для x в интервале 0,
1,5
и в зависимости от числа k обратных
функций выделим следующие интервалы
для Y (рис. 1.1):
Рис. 1.1
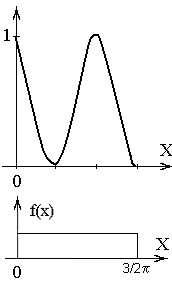
(0, 1) k =1,
(1, +¥) k = 0.
Так как на интервалах (-¥, 0) и (1, +¥) обратная функция не существует, то g(y)=0.
В интервале (0,1) одна обратная функция
y1(y)
=
:
,
.
Таким образом, плотность вероятности величины Y равна:
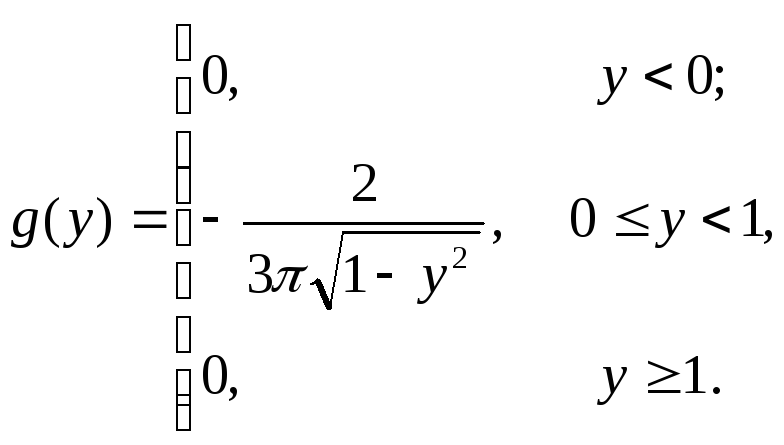
В задачах 8.1-8.30 (конкретные параметры приведены в табл. 1.4) двумерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 1.2 области B. Двумерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
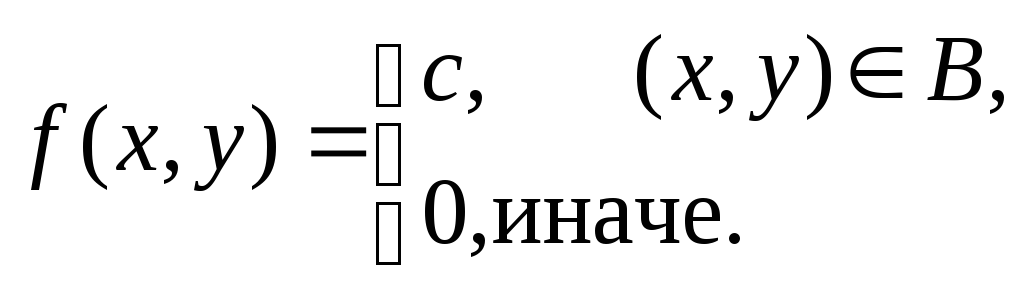
Вычислить коэффициент корреляции между величинами X и Y.
Таблица 1.4
|
Вариант |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
y1 |
y2 |
|
8.12 |
0 |
2 |
5 |
4 |
5 |
6 |
1 |
2 |