Министерство образования Республики Беларусь
Учреждение образования
«БЕЛАРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»
Кафедра вычислительных методов и программирования
Контрольна работа по
«теории вероятностей и математической
статистике»
Студентки ЗиДФ
Специальности ЭиОП
гр.201502-38
Сенькевич Светланы Иосифовны
Номер договора 253-с
От 8 июля 2010г.
17.08.2010
Задача 1.15
Наудачу взяты два положительных числа
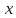и
,
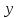причем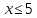
,
.
Найти вероятность того, что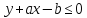
и
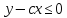
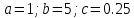
Решение:
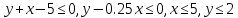
Кроме того, по условию
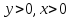
Воспользуемся геометрическим определением вероятности.
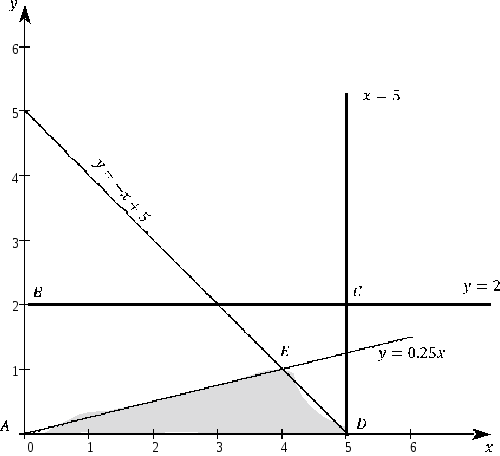
Искомая вероятность:
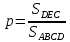
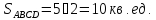
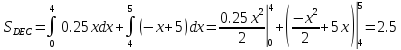
Искомая вероятность:
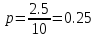
Ответ:
.+
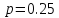Задача 2.23
Приведены схемы соединения элементов,
образующих цепь с одним входом и одним
выходом. Предполагается, что отказы
элементов являются независимыми в
совокупности событиями. Отказ любого
из элементов приводит к прерыванию
сигнала в той ветви цепи, где находится
данный элемент. Вероятности отказа
элементов 1, 2, 3, 4, 5 соответственно равны
;
;
;
;
.
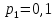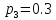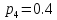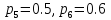Найти вероятность того, что сигнал
пройдет со входа на выход.
Решение:
Пусть событие
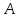-сигнал пройдет со входа на выход.
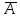-сигнал не пройдет со входа на выход.
Это произойдет в том случае, если откажут
все 5 элементов.
Тогда:
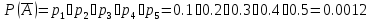
Так как события
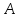и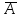
образуют полную группу событий, то:
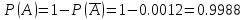
Ответ: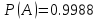
.
+
Задача 3.24
Прибор состоит из трех блоков. Исправность каждого блока необходима для функционирования устройства. Отказы блоков независимы. Вероятности безотказной работы блоков соответственно равны 0,6; 0,7; 0,8. В результате испытаний один блок вышел из строя. Определить вероятность того, что отказал первый блок.
Решение:
Наблюдаемое событие
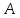-в результате испытаний один блок вышел
из строя
До опыта возможны следующие гипотезы:
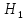-отказал 1-й блок
-отказал 2-й блок
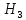-отказал 3-й блок
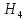-отказал 1-й и 2-й блок
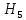-отказал 2-й и 3-й блок
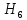-отказал 1-й и 3-й блок
-отказал 1-й, 2-й и 3-й блок
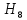- ни одного блока не отказало
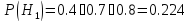
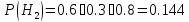
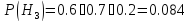
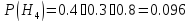
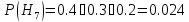
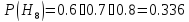
Запишем условные вероятности:
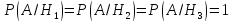
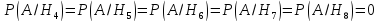
Тогда:
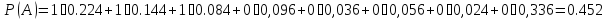
По формуле Бейеса найдем вероятность того, что отказал первый блок:
+
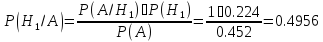Ответ: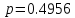
.
Задача 4.24
Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что будет хотя бы пять попаданий в мишень.
Решение:
Воспользуемся формулой Бернулли:
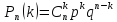
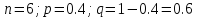
Пусть событие
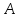-в мишень попали хотя бы пять раз. Это
значит пять или шесть раз.
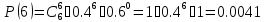
Искомая вероятность:
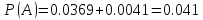
Ответ: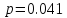
.
+
Задача 5.23
Дискретная случайная величина Х может
принимать одно из пяти фиксированных
значений
,
,
,
,
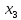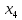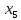с вероятностями
,
,
,
,
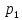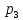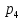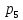соответственно. Вычислить математическое
ожидание и дисперсию величины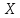
.
Рассчитать и построить график функции
распределения.
|
|
-10 |
-4 |
0 |
4 |
10 |
|
|
0.2 |
0.2 |
0.2 |
0.2 |
0.2 |
Решение:
Вычислим математическое ожидание:
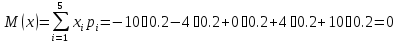
Дисперсию найдем по формуле:
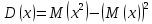
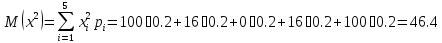
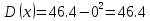
Функция распределения
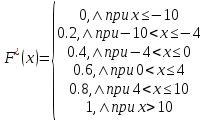
График эмпирической функции распределения
+
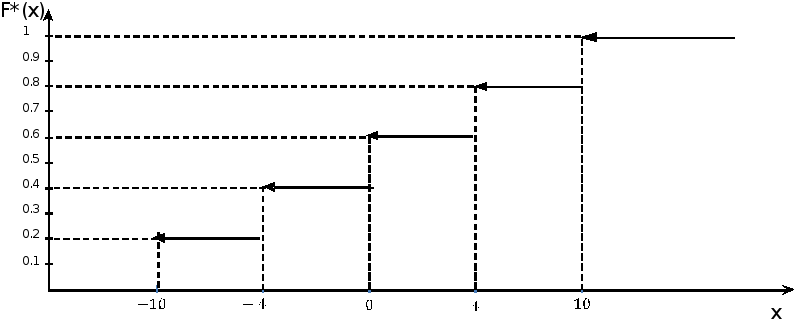
Задача 6.11
Случайная величина Х задана плотностью вероятности
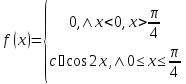
Определить константу
,
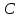математическое ожидание, дисперсию,
функцию распределения величины
,
а также вероятность ее попадания в
интервал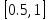
.
Решение:
Константу
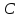определим, используя свойство плотности
вероятности:
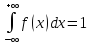
В нашем случае:
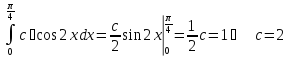
Найдем математическое ожидание:
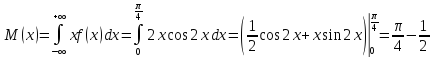
Найдем дисперсию:
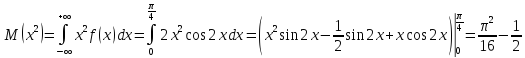
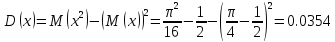
Найдем функцию распределения:
для
:
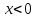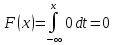
для
:
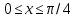для
:
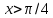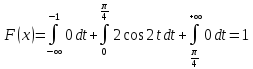
Функция распределения:
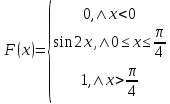
Вероятность попадания в интервал
:
+
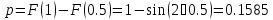Задача 7.28
Случайная величина
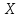распределена равномерно на интервале
.
Построить график случайной величины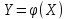
и определить плотность вероятности
.
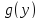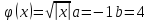
Решение:
Построим график
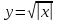
Найдем плотность распределения
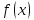случайной величины
:
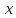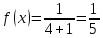
в интервале
вне этого интервала
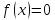
Функция
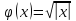на интервале
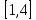имеет одну обратную функцию
На интервале
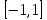две обратные функци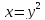и:
и
Искомая плотность распределения может быть найдена по формуле:
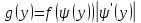
На интервале
,
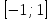так как
Плотность распределения:
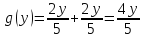
На интервале
так как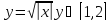
Плотность распределения:
Таким образом:
+
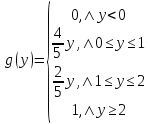Задача 8.19
Двухмерный случайный вектор
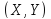равномерно распределен внутри выделенной
жирными прямыми линиями на рисунке
области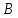
.
Двумерная плотность вероятности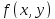
одинакова для любой точки этой области
:
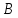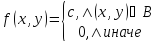
Вычислить коэффициент корреляции между
величинами
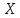и
.
Решение:
Запишем в аналитической форме совместную плотность вероятностей:
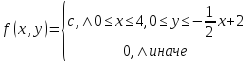
Определим
,
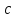используя условие нормировки:
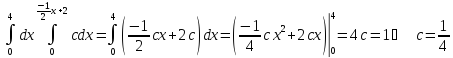
Найдем математическое ожидание и
дисперсию величины
:
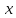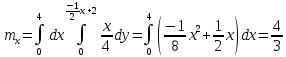
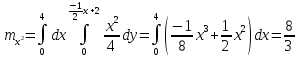
Тогда дисперсия:
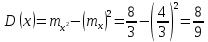
Найдем математическое ожидание и
дисперсию величины
:
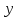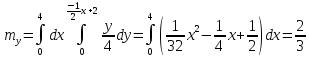
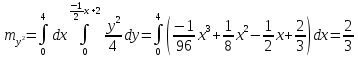
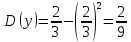
Определим корреляционный момент:
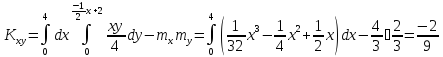
Коэффициент корреляции:
+
Задача 9.14
Вычислить математическое ожидание и
дисперсию величин
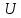и
,
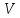а также определить их коэффициент
корреляции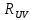
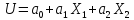
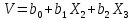
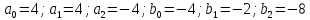
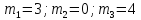
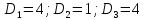
Решение:
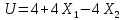
Вычислим математические ожидания:
Дисперсии:
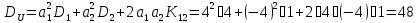
Корреляционный момент
Определим математическое ожидание
произведения величин
и
:
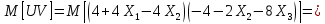
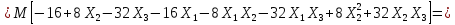
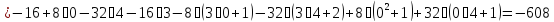
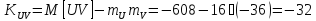
Коэффициент корреляции:
+
Задача 10.93
По выборке одномерной случайной величины:
- получить вариационный ряд;
- построить на листе формата А4 график эмпирической функции распределения F*(x);
- построить гистограмму равноинтервальным способом;
- построить гистограмму равновероятностным способом;
- вычислить точечные оценки математического ожидания и дисперсии;
- вычислить интервальные оценки
математического ожидания и дисперсии
;
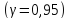- выдвинуть гипотезу о законе распределения
случайной величины и проверить ее при
помощи критерия согласия
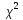и критерия Колмогорова (
).
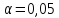График гипотетической функции
распределения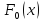
и построить совместно с графиком
в той же системе координат и на том же
листе.
|
0.02 |
-2.79 |
-3.65 |
-4.5 |
-3.69 |
-2.29 |
-0.01 |
-1.54 |
-2.35 |
-3.21 |
|
0.71 |
-3.56 |
-0.49 |
-0.22 |
-4.23 |
-4.17 |
-3.03 |
-2.58 |
-2.07 |
-3.59 |
|
-1.55 |
-3.86 |
0.77 |
-0.62 |
-4.01 |
-0.62 |
-2.69 |
-0.22 |
-0.81 |
-2.27 |
|
-0.32 |
0.36 |
-3.04 |
0.07 |
-2 |
-1.72 |
0.5 |
-1.72 |
-1.25 |
0.43 |
|
-3.75 |
-2.3 |
-3.13 |
-0.07 |
-2.52 |
-2.04 |
-2.75 |
-0.6 |
-0.98 |
-0.51 |
|
-3.11 |
-0.02 |
-0.89 |
-1.21 |
-2.65 |
-4.44 |
-1.06 |
-3.7 |
-0.58 |
-3 |
|
-0.03 |
-0.92 |
-2.01 |
-1.57 |
-1.02 |
-4.16 |
-3.03 |
-0.28 |
-1.49 |
-2.26 |
|
-0.08 |
0 |
-2.81 |
0.68 |
-1.26 |
-2.26 |
-3.42 |
-2.53 |
0.32 |
-3.72 |
|
-2.68 |
-3.89 |
-3.1 |
-1.19 |
-3.36 |
-3.79 |
-1.48 |
-0.19 |
0.76 |
-3.44 |
|
-1.74 |
-2.43 |
-3.46 |
-0.84 |
-3.33 |
-0.34 |
-3.92 |
-1.11 |
-3.32 |
-0.07 |