3.Матеметическое ожидание св, его свойства.

Математическим ожиданием случайной величины называется число

Свойства математического ожидания.

М1. , если С-const. Для С ,

M2.

М3.

М4. , если и - независимые случайные величины.

Пусть и - непрерывные случайные величины. Тогда

М5. Если с вероятностью 1 , то

; .

если: 1) с вероятностью 1, то ; 2) с вероятностью 1, то

М6.

Результат опирается на известное интегральное неравенство .

М7. - неравенство Коши-Буняковского.

Рассмотрим с. величину λξ + η: квадратный трехчлен неотрицателен относительно λ, следовательно, его дискриминант не положителен:

.

М8. Если , то .

Билет 18

1.Локальная теорема Муавра-Лапласа

Если в схеме Бернулли число испытаний – n велико, то для всех m справедливо приближенное равенство , где , где функцию называют плотностью стандартного нормального распределения.

Так как , где .

.

Обозначим через ; , если x – ограниченная величина.

Далее ;

.

Отсюда . .

2.Непрерывные случайные величины – основные определения. Основные свойства плотности распределения.

Функция , такая что (предполагается, что интеграл сходится). называются плотностью распределения случайной величины .

Непрерывной случайной величиной называется случайная величина, функция распределения которой F(x) представима в виде интеграла .

На практике функция плотности распределения является непрерывной почти всюду на области определения, потому почти всюду справедливо равенство

Для непрерывных случайных величин плотность распределения – основная характеристика случайной величины, она определяет закон распределения случайной величины.

Свойства плотности распределения:

1. . что функция распределения F(x) – неубывающая функция.

2. По определению

3. .

3. Характеристическая функция. Теорема единственности. Формула обращения.

Характеристической функцией с. величины называется функция:

Теорема (единственности). Пусть F и G две функции распределения, имеющие одну и ту же характеристическую функцию. Тогда F = G.

Теорема (формула обращения). Пусть F – функция распределения с. величины и g – ее характеристическая функция . Тогда

а) для любых двух точек x и y, x<y, в которых функция F непрерывна, имеет место соотношение: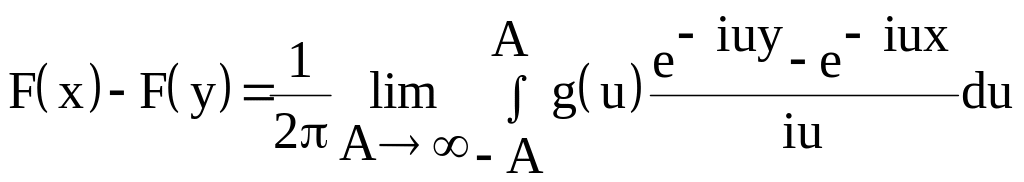

справедлива и в точках разрыва функции F, если считать , что в этих точках

б) есл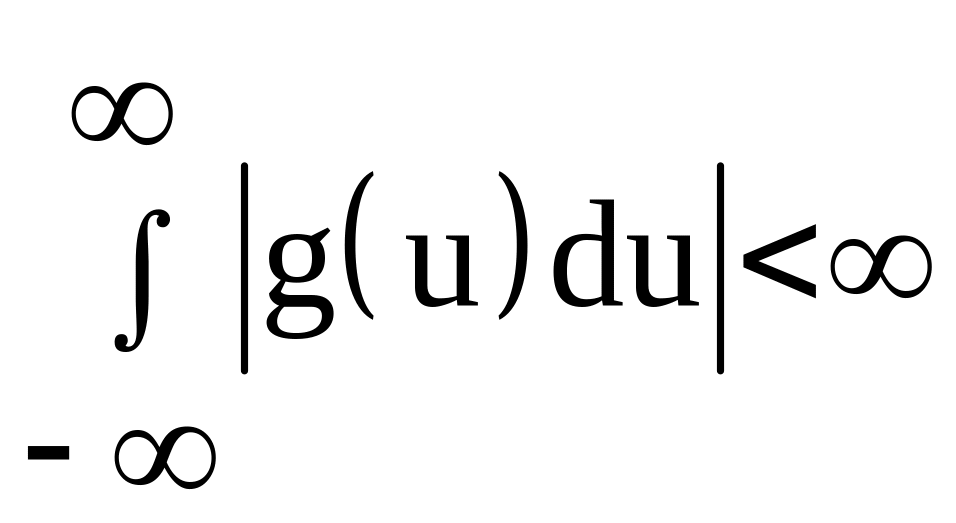и , то функция распределения имеет плотность f и

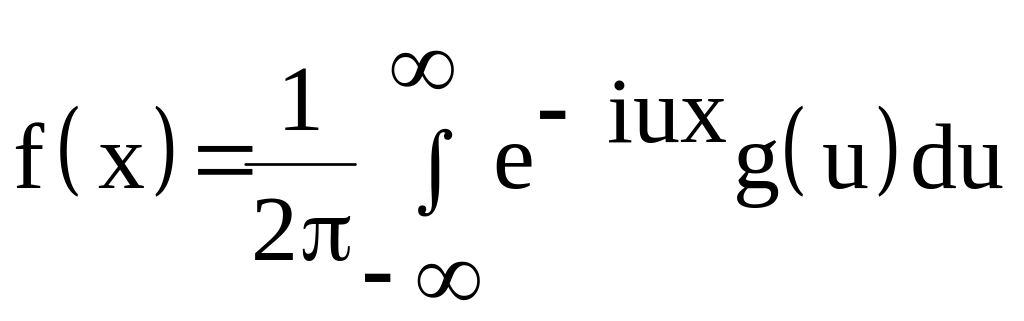(3.57)

Билет 19

1. Независимые события: определения, свойства. Формула умножения вероятности.