Формула умножения вероятностей
2. Дискретные случайные величины определение, ряд распределения, функция распределения, примеры.
Случайная величина
называется дискретной, если она
каждому элементарному исходу ставит в
соответствие одно число из конечного
или счётного множества чисел
,
причём вероятность события
Набор вероятностей
называют рядом распределения с. величины.
Если при описании случайной величины применяют какую-нибудь другую её характеристику вместо функции распределения и при этом по характеристике возможно однозначно восстановить функцию распределения, то такая характеристика называется законом распределения случайной величины или просто распределением случайной величины.
,
где
,
если
и
,
если
.
Постоянная величина
С. Она принимает единственное значение
с вероятностью, равной единице.
Индикатор события А.
- дискретное вероятностное пространство
и
–с. величина, принимающая значения
.
,
то
,
где множества
образуют разбиение пространства
– они попарно не пересекаются и их сумма
равна
.
Ряд распределения с. величины
имеет вид:
-
0
1
P
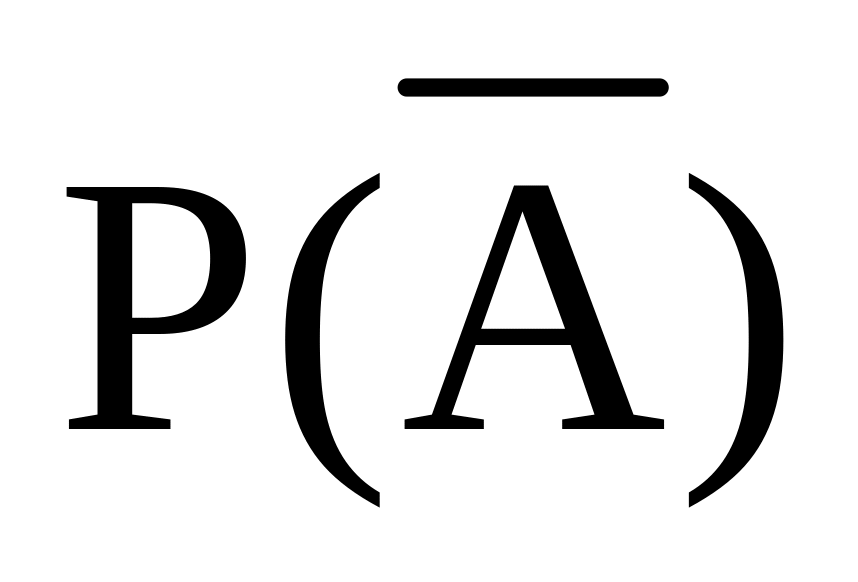
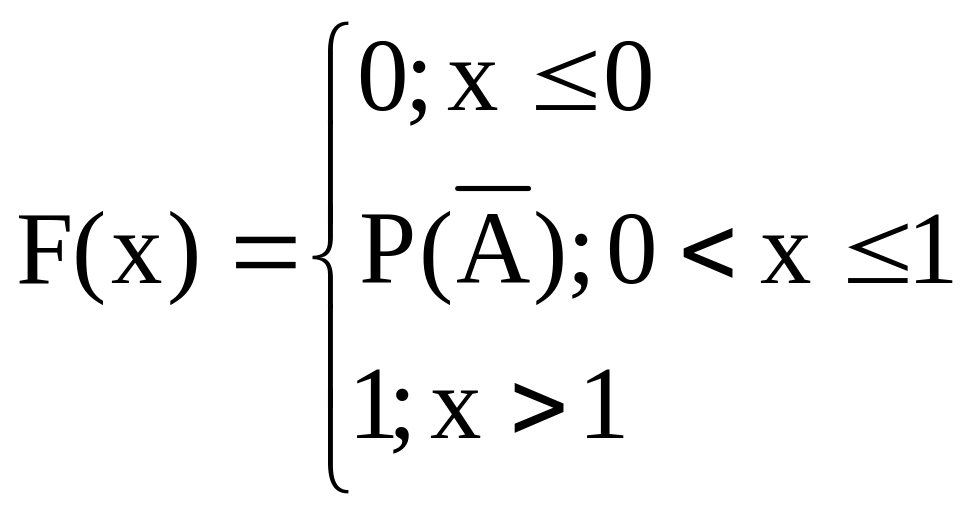
3. Характеристическая функция, её свойства.
Характеристической функцией с. величины называется функция:
Некоторые свойства характеристических функций
1.
так как
2. Характеристическая функция g(u) – равномерно непрерывная функция по u .
-сходится Функция на отрезке [-N, N] равномерно непрерывна по h
Окончательно,
Так как не зависит от ε, то это доказывает равномерную непрерывность функции g(u).
3. .
4. Характеристическая функция является функцией действительного переменного тогда и только тогда, когда распределение F симметрично (то есть ).
5. Если существует абсолютный начальный момент порядка N, то характеристическая функция с. величины дифференцируема N раз, при этом
Так как то равномерно по u сходится, значит, его можно дифференцировать:
Если k=1, то g (u)=
6. Если существует и конечна , то .
Тогда, согласно свойству 5, существуют моменты всех порядков до N=2n включительно и .
7. Для того чтобы с. величины ξ и η была независимы, необходимо и достаточно чтобы характеристическая функция суммы этих с. величин была равна произведению их характеристических функций.
8. Если = a +b, то
Билет 6
1.Формула полной вероятности
- вероятностное пространство и события
образуют в нем полную группу событий:1)
;
2)
;
3)
.
События
часто при этом называют гипотезами.
,
из условия
.
.
Формула справедлива для счетного набора гипотез , если они удовлетворяют условиям 1)-3).
2. Пуассоновское распределение: определение, обозначение, производящая функция распределения и её использование для нахождения числовых характеристик распределен.
Cлучайная
величина
распределена по закону Пуассона, если
она принимает неотрицательные целые
значения с вероятностями
- параметр распределения Пуассона.
Характеристической функцией с. величины называется функция:
Пусть
и – независимые
с. величины, распределенные по закону
Пуассона с параметрами
и
.Для
них
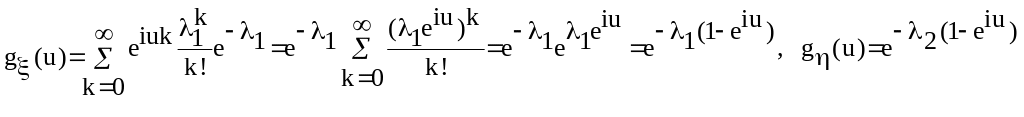
3.Условное математическое ожидание. Кривые регрессии на примере двумерной св.
Условным математическим
ожиданием с. величины
при
условии, что
,
называется величина: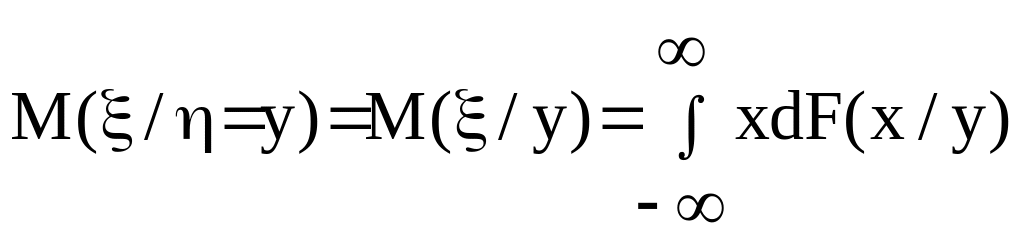 
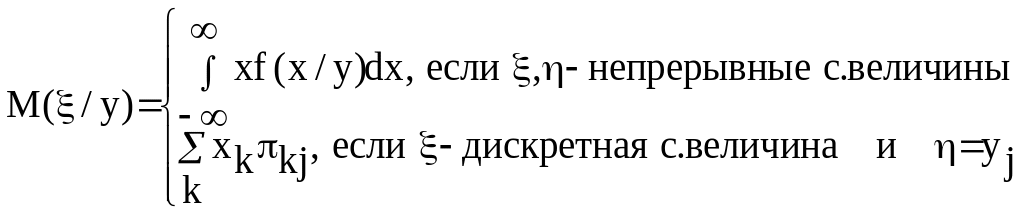
Величина
является
функцией с. величины
(см. формулу 3.44), следовательно, сама
является с. величиной, которую мы будем
обозначать M(/).
Область определения с. величины M(/)=y
= M(/y)
совпадает с множеством значений с.
величины
.