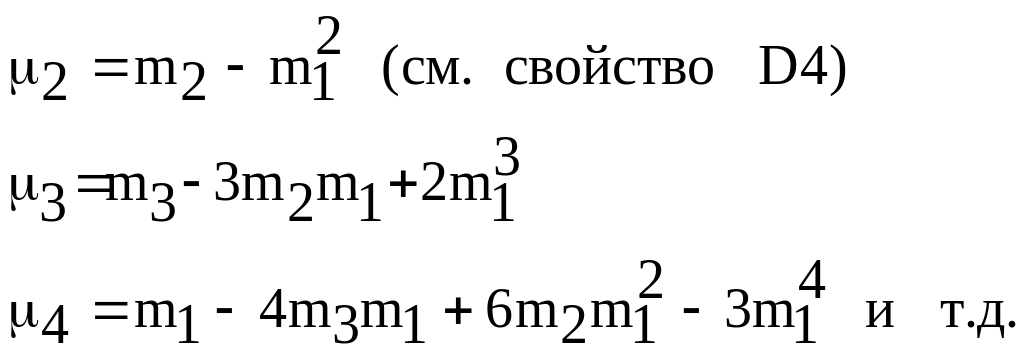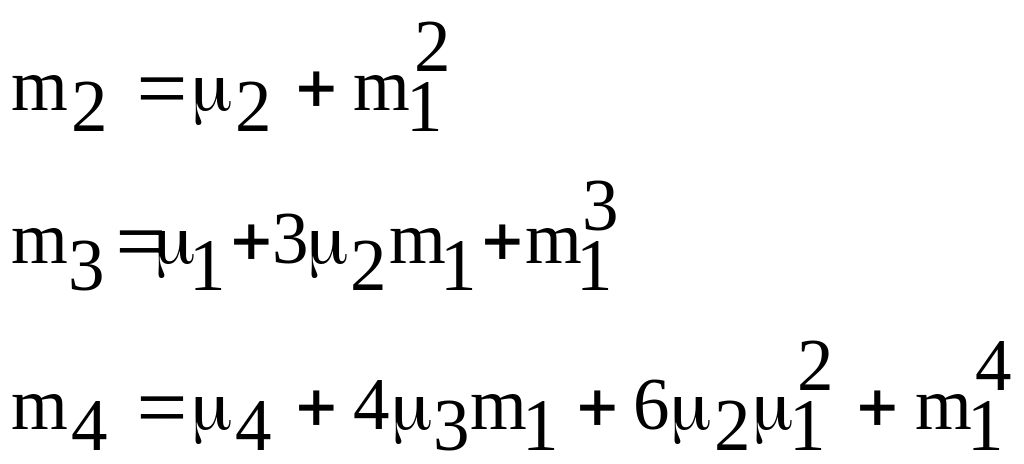Формула умножения вероятностей

События А и В называются независимыми, если Свойства независимых событий

1. или

2. Если события А и В независимы, то независимы события А и , и В, и .

. ; .

3. Если события А и , А и независимы и , то независимы и события А и .

4. Если события независимы в совокупности, то

События называются независимыми в совокупности, если для всех k=2,…,n, , то есть , ; , и т.д.

5. Пусть - независимые в совокупности события и .

и события , k=1,…,n, независимы в совокупности (свойство 2 независимых событий). Тогда по формуле (1.6) имеем .

формула вероятности суммы независимых в совокупности событий.

2.Непрерывные случайные величины – основные определения. Основные свойства плотности распределения.

Функция , такая что (предполагается, что интеграл сходится). называются плотностью распределения случайной величины .

Непрерывной случайной величиной называется случайная величина, функция распределения которой F(x) представима в виде интеграла .

На практике функция плотности распределения является непрерывной почти всюду на области определения, потому почти всюду справедливо равенство

Для непрерывных случайных величин плотность распределения – основная характеристика случайной величины, она определяет закон распределения случайной величины.

Свойства плотности распределения:

1. . что функция распределения F(x) – неубывающая функция.

2. По определению

3. .

3. Ковариация случайных величин, её свойства.

Ковариацией с. величин  и  называют математическое ожидание произведения центрированных с. величин и :

cov( ,)=

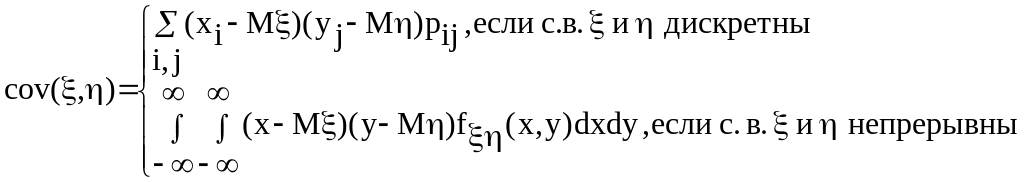
Если cov(,)=0, то с. величины ξ и η называются некоррелированными.

Если ξ и η двумерные с. величины, то cov( ,) определяется по формуле:

cov(,)= .

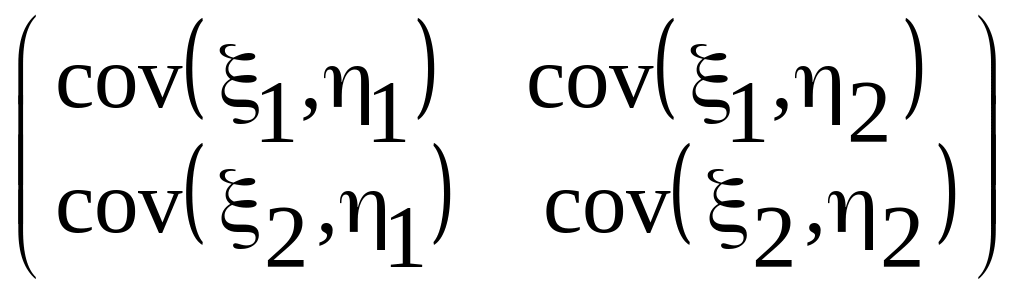Ковариация с. величин обладает следующими свойствами:

1. cov (,) = D cov (,) = M( - M)² = D

2. Если  и  независимы, то cov(,) = 0.

cov(,) = M( - M)( - M) = M( - M)M( - M)=0

3.Пусть .Тогда

ξ и η двумерные с. величины, то есть , при этом , где - неслучайные матрицы порядка 2×2, - двумерные неслучайные векторы, тогда .

4. . Рассмотрим с. величину  = x -  , x – произвольное число.

.

ξ и η – двумерные с. величины, то и Dξ= tr coν(ξ,ξ), Dη= tr coν(η,η).

5. .

Билет14

1. Геометрическая вероятность: определение, примеры, свойства.

1. Множество Ω рассматривается как некоторое непрерывное ограниченное множество с бесконечным числом элементов, например, отрезок, многоугольник, шар и т.д. (вид множества определяется условиями задачи);

2. Опыт состоит в бросании идеальной точки (не имеет ни размера, ни веса) в это множество Ω;

3. Вероятность попадания ее в какую-нибудь область А Ω пропорциональна мере этой области μ(А).

Тогда вероятность наступления события А определяется как:

Р(А)= μ(А)/μ(Ω)

2. Дискретные случайные величины определение, ряд распределения, функция распределения, примеры.

Случайная величина называется дискретной, если она каждому элементарному исходу ставит в соответствие одно число из конечного или счётного множества чисел , причём вероятность события Набор вероятностей называют рядом распределения с. величины.

Если при описании случайной величины применяют какую-нибудь другую её характеристику вместо функции распределения и при этом по характеристике возможно однозначно восстановить функцию распределения, то такая характеристика называется законом распределения случайной величины или просто распределением случайной величины.

, где , если и , если .

Постоянная величина С. Она принимает единственное значение с вероятностью, равной единице.

Индикатор события А.

- дискретное вероятностное пространство и –с. величина, принимающая значения . , то , где множества образуют разбиение пространства – они попарно не пересекаются и их сумма равна . Ряд распределения с. величины имеет вид:

	0	1
P

3. Производящие функции: определение, основные свойства. Примеры

Производящей функцией для дискретно распределенной с. величины ξ называется функция

1. Если производящие функции двух с. величин совпадают, то совпадают и распределения этих с. величин.

2. .

3. Если ξ и η – независимые с. величины, то производящая функция произведения этих с. величин равна произведению производящих функций сомножителей.

Действительно, . Далее, .

Билет 15

1.Статическая вероятность событий. Теореме Бернулли.

В основе статистического определения вероятности лежит опытный факт – так называемая устойчивость частот.

частота осуществления какого-либо исхода в последовательности экспериментов, проводимых в одинаковых условиях, приближается к некоторому числу p [0,1].

каково бы ни было ε > 0 с ростом n вероятность того, что частота события отличается от некоторого постоянного числа p [0,1] не более чем на ε, стремится к 1.

Относительной частотой события А назовем отношение числа опытов, в которых событие А произошло, к числу проведенных опытов: Вероятность события А приближенно равна относительной частоте этого события. Чем больше число n, тем точнее равенство: P(A) . Это и есть статистическое определение вероятности. Статистическое определение вероятности является единственным способом приближенного вычисления вероятности.

2. Пуассоновское распределение: определение, обозначение, производящая функция распределения и её использование для нахождения числовых характеристик распределен.

Cлучайная величина распределена по закону Пуассона, если она принимает неотрицательные целые значения с вероятностями

- параметр распределения Пуассона.

Производящей функцией для дискретно распределенной с. величины ξ называется функция

1. Если производящие функции двух с. величин совпадают, то совпадают и распределения этих с. величин.

2. .

3. Если ξ и η – независимые с. величины, то производящая функция произведения этих с. величин равна произведению производящих функций сомножителей.

Действительно, . Далее, .

, .

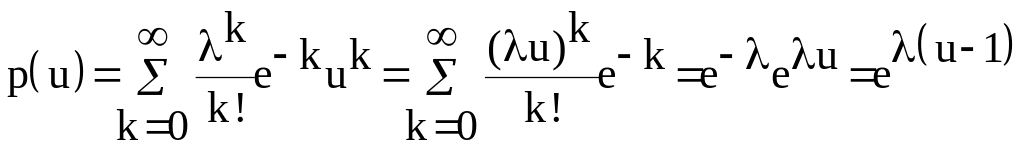3.Дисперсия случайной величины, её свойства

Дисперсией с. величины  называют число: D=M(-M)²

() =σ = называется средним квадратичным отклонением с. величины ξ.

D =

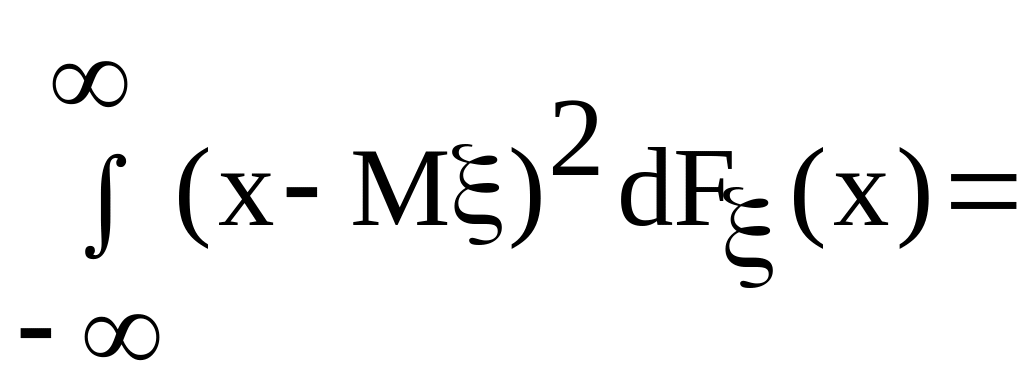
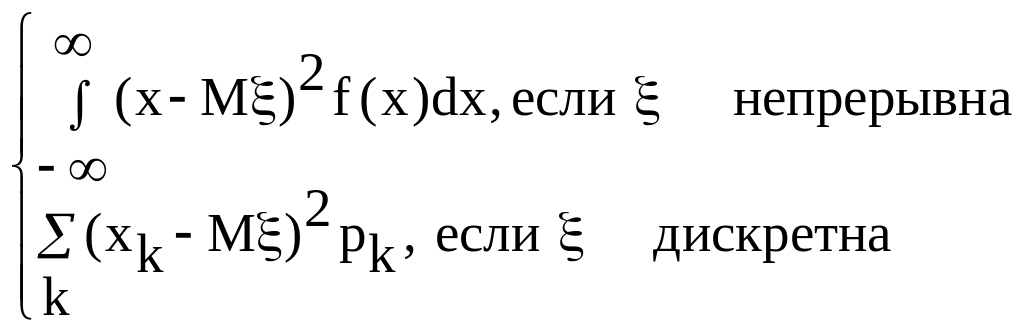
Свойства дисперсии.

D1. если

D2.

D3. , если величины независимы

, если независимы.

D4.

Следствия. ; ; .

D5.

Билет 16

1.Свойства вероятности.

Р1. .

Р2. . ,

Р3. Если , то .

. Так как , то . Отсюда, .

Следствие. если , то .

Р4. .

Р5. - формула вероятности суммы событий.

,

и или .

Р6. .

Р7. .

Если же , тогда .

Р8. . События несовместны при ; , равенство имеет место, если . Тогда .

Р9. Если монотонная последовательность событий и , если , ; , если , , то .

вероятностей: .

2. Экспоненциальное распределение: определение, обозначение. Производящая функция распределения, её использование для вычисления числовых характеристик.

– параметр распределения

Экспоненциально распределенная случайная величина обладает свойством - отсутствием последствия.

если непрерывная случайная величина обладает этим свойством, то вероятность попадания в любой интервал длины не зависит от того, где на числовой прямой расположено начало интервала, эта вероятность зависит только от длины интервала.

Производящей функцией для дискретно распределенной с. величины ξ называется функция .

свойства производящих функций:

1. Если производящие функции двух с. величин совпадают, то совпадают и распределения этих с. величин.

2. .

3. Если ξ и η – независимые с. величины, то производящая функция произведения этих с. величин равна произведению производящих функций сомножителей.

Ценность производящих функций заключается в связях производных этой функции с математическими ожиданиями и дисперсиями с. величин- свойство 2. Так как , то

3.Моменты св, α-квантиль, мода, медиана.

Начальным моментом порядка c. величины называется число:

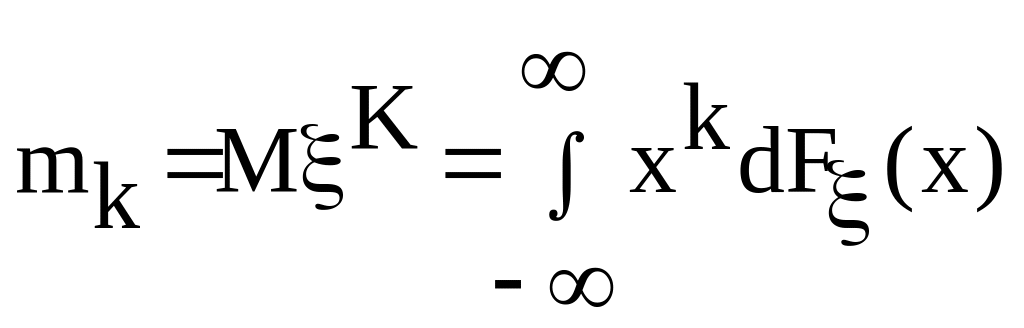
При математическое ожидание – начальный момент 1-го порядка.

Центральным моментом порядка c. величины называется число:

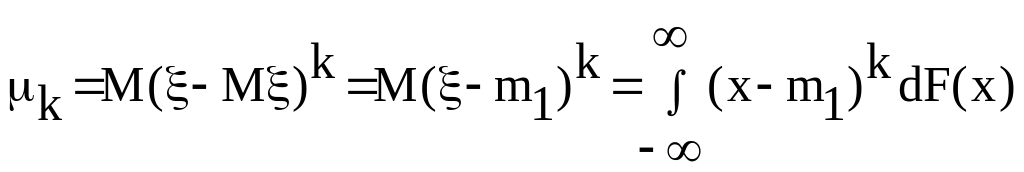
При дисперсия с. величины – это центральный момент 2 порядка. Интересно отметить, что

k-й момент с. величины называются абсолютным к-м моментом с. величины ξ.

Между начальными и центральными моментами существуют связывающие их соотношения:

- с. величины с совместной функцией распределения . Величины , называются смешанными моментами величин порядка k.

Центральные смешанные моменты к-го порядка .

Центральные смешанные моменты 2 порядка с. величин ξ и η -

Медиана с.величины определяется из соотношения . это любое решение уравнения . Поскольку решение этого уравнения не единственно, то медиана с. величины определяется неоднозначно.

Модой непрерывной с величины называют точку локального максимума плотности распределения f(x).

Модой дискретной с. величины называют такое её значение , для которого и , при этом все её значения должны быть расположены в порядке возрастания.

-квантилью с. величины  называется число, удовлетворяющее уравнениям: ( ).

Билет17

1. Условная вероятность Показать, что условная вероятность удовлетворяет аксиомам вероятности. Формула умножения вероятностей.

Вероятность события А при условии, что в опыте произошло событие В, называют условной вероятностью.

– вероятностное пространство. Если , , то число называют условной вероятностью события А при условии В.

При фиксированном событии , Р(А/В) является функцией событий .

1) - следует из определения. 2) , так как . 3) Пусть последовательность попарно несовместных событий. Тогда .

Если исходная вероятностная мера задана на измеримом пространстве , то условная вероятностная мера задана на измеримом пространстве , где - σ-алгебра ω-множеств вида , .

формула умножения вероятностей

2. Случайная величина. Функция распределения св, основные её свойства.

– вероятностное пространство. Случайной величиной называется измеримая функция , ставящая в соответствие каждому элементарному исходу число . Функцией распределения случайной величины называется функция , значение которой в точке x равно вероятности события , то есть

Основные свойства функции распределения.

F1. поскольку F(x) – вероятность.

F2. F(x) – неубывающая функция, то есть если , то .

событие входит в событие при условии . Тогда или .

F3.

Событие - невозможное событие, поэтому .

Событие - достоверное событие, поэтому .

F4. F(x) – непрерывная слева функция в каждой точке х.

возрастающая последовательность чисел, сходящаяся к . События и . , последовательность монотонная и ее предел . .

F5. .

объединение двух несовместных событий и . Из следует .

F6. .

По определению , где – убывающая последовательность, . Поскольку , согласно свойству непрерывности вероятности F7. .

Так как и , то .

На основании свойств F1-F7 могут быть получены важные для практических целей результаты, а именно:

(2.2)

Так как