Свойства условного математического ожидания.

1. M(C) = C

2. M(a + b) = aM() + b

3. M( + ) = M() + M()

4. M() = M()M(),если  и  независимы при условии ν.

5. M[ M()]=M

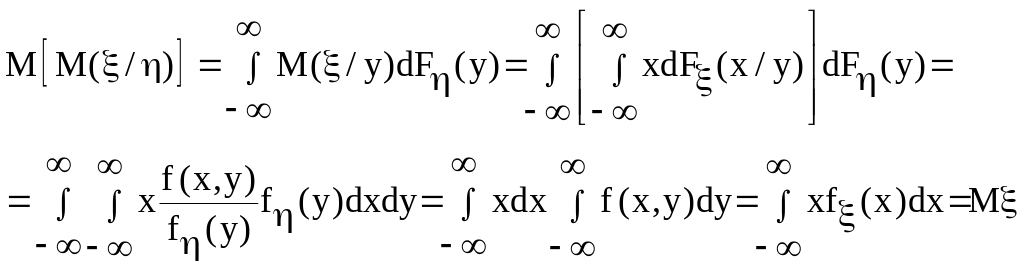
, формула полного математического ожидания.

6. , h и  – некоторые функции

7. M(/) = M, если  и  - независимы.

.

8.

Функцию M( /) называют функцией регрессии или просто регрессией с. величины  на с. величину . График функции M( /) называют линией регрессии с. величины  на с. величину . Линий регрессии две M( /) и M( /). В общем случае они между собой не совпадают.

M(/) На плоскости (y,х) уравнение этой прямой имеет вид х=a+by. M(/)= с+ dx, где с= ,

, для регрессии η на ξ и регрессии на η соответственно. Прямые регрессии проходят через центр рассеивания – точку ( ) с угловым коэффициентом . Так как |ρ| ≤1, то | | ≥ | |, что означает, что прямая регрессии всегда расположена более круто по отношению к оси Ох, чем вторая регрессия. При |ρ| =1 они совпадают, при ρ =0 прямые распадаются на две прямые, параллельные осям координат – вырожденный случай регрессии.

Билет 7

1.Формула Байеса

, k=1,…,n, - априорные вероятности гипотез, а , k=1,…,n, - апостериорные вероятности гипотез после того, как произошло событие А.

2. Геометрическое распределение: определение, обозначение. Характеристическая функция и её применение для вычисления числовых характеристик.

– число испытаний, которое необходимо провести, прежде чем появится первый успех. В каждом отдельном испытании успех достигается с вероятностью р.

Случайная величина может принимать счетное множество значений k=0,1,2,3…,n,…

Если , то в первых k испытаниях появилась неудача, а в (k+1) испытании – успех. , .

Характеристической функцией с. величины называется функция:

3. Непрерывные n-мерные св. Свойства совместной плотности распределения. Если функция абсолютно непрерывна, то случайная величина называется непрерывной. Совместная функция и функция плотность распределения n-мерной случайной величины x.

(3.7)

Свойства совместной плотности распределения:

1. ;

2. ;

3. ;

4. ; .

Билет 8

1. Схема Бернулли, формула Бернулли.

Схема Бернулли - это эксперимент, удовлетворяющий условиям: 1) за основу берется эксперимент, имеющий 2 исхода. 2) этот исходный эксперимент повторяется независимо n раз (исходы эксперимента при очередном повторении не зависят от исходов эксперимента на предыдущих шагах) 3) вероятности двух исходов при каждом повторении исходного эксперимента одни и те же.

А– в n испытаниях произошло m успехов, m=0,1,2,…,n. В элементарных событиях, благоприятствующих событию А, буква У в последовательности УНУУ…Н встречается ровно m раз. Вероятность такого элементарного события равна . Число таких элементарных событий совпадает с числом способов, которыми можно расставить m букв У по n местам, при этом все буквы У неразличимы. .

2. Биноминальное распределение: определение, обозначение. Производящая функция распределения и её применение для вычисления числовых характеристик.

Случайная величина – число успехов в серии из n независимых испытаний. Она может принимать значения . Восстановим функцию распределения F(x). Поскольку , то для всех событие - невозможное, значит . Если , то событие состоит из тех элементарных исходов , для которых , . Если , то событие состоит из тех элементарных исходов , для которых или , , , и т. д. При событие достоверное событие и .

Производящей функцией для дискретно распределенной с. величины ξ называется функция

1. Если производящие функции двух с. величин совпадают, то совпадают и распределения этих с. величин.

2. .

3. Если ξ и η – независимые с. величины, то производящая функция произведения этих с. величин равна произведению производящих функций сомножителей.

Действительно, . Далее, .

Пусть ξ имеет биномиальный закон распределения Найти р(u).

.

Билет 9

1.Формула Пуассона.

Если число испытаний в схеме Бернулли n велико, вероятность успеха в одном испытании p мала и мало также число , тогда

.

Здесь ;

Теорема Пуассона справедлива и по отношению к числу неудач, но только в этом случае должно быть мало число .

.

События при различных m в схеме Бернулли несовместны. Тогда вероятность появления успеха в n испытаниях не менее раз, но не более раз:

Вероятность появления хотя бы одного успеха в серии из n независимых испытаний получаем из предыдущей формулы заменой в ней на 1 и на n: