Билет1

1.Пространство элементарных исходов. События. Измеримое пространство.

пространство элементарных событий – это множество событий, удовлетворяющих условиям: 1) в результате эксперимента обязательно появляется одно из этих событий; 2) появление одного события исключает появление другого; 3) в условиях данного опыта эти события не могут быть разделены на более мелкие.

событие – это исход опыта, представимый в виде подмножества элементарных событий.

Измеримое пространство обозначают символом (Ω, F). где Ω - пространство элемнтар. исходов эксперимента, σ-алгебра F выделяет класс событий – все ω-множества из Ω, не входящие в F.

2.Непрерывные случайные величины. Нормально распределённые случайные величины определение, обозначение, характеристическая функция, её применение для вычисления числовых характеристик нормального распределения

Непрерывной случайной величиной называется случайная величина, функция распределения которой F(x) представима в виде интеграла . Для неё плотность распределения – основная характеристика случайной величины, она определяет закон распределения случайной величины.

Случайная величина имеет нормальное распределение, если плотность распределения имеет вид 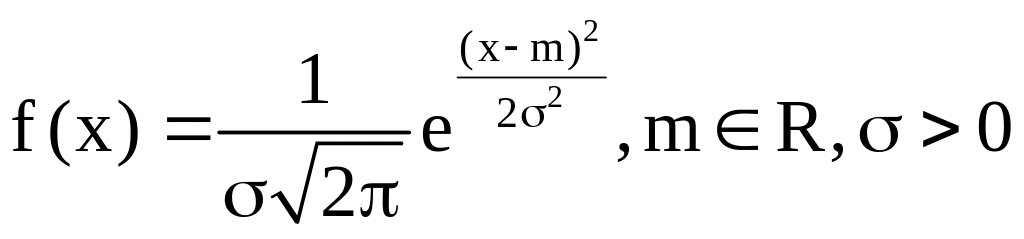- параметры распределения, m – средним значением случайной величины, – средним квадратичным отклонением. Нормальная случайная величина практически никогда не отклоняется от своего среднего значения m более чем на . Если , , то такой нормальный закон называют стандартным нормальным законом распределения. и . Хар-ой функцией с. величины называется функция:

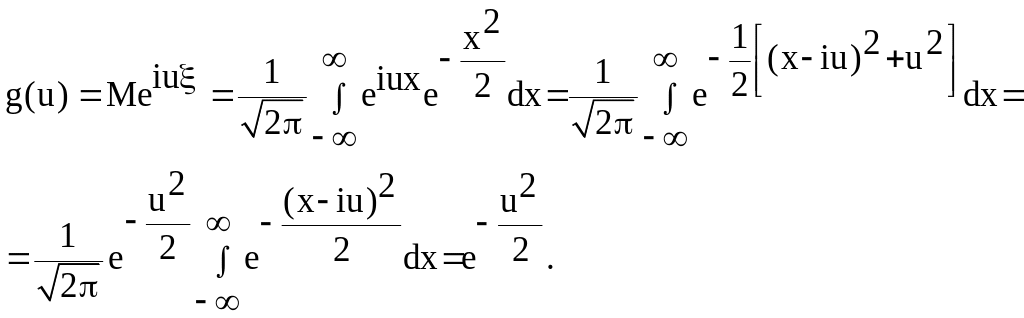
3.Многомерная функция распределения, её свойства для n=2.

- некоторое вероятностное пространство и - случайные величины, заданные на нем. Каждому значению они ставят в соответствие вектор .Отображение , задаваемое совокупностью случайных величин , называется случайным вектором

все , измеримые функции, случайным вектором следовало бы назвать отображение , где – борелевская -алгебра в . Необходимым и достаточным условием измеримости случайного вектора является выполнение условия: .

Основной характеристикой случайного вектора является n-мерная функция распределения: .

1. ;

2. - неубывающая функция по каждому из своих аргументов;

3. - непрерывная слева функция по каждому из своих аргументов;

4. ;

5. ;

6. ; ; ;

7. .

Эту формулу можно вывести, исходя из представления события в виде алгебраической суммы событий: .

Билет2

1. Алгебра и σ-алгебра. Примеры. Измеримые пространства.

Ω – пространство э. событий некоторого (с. эксперимента). Любое подмножество множества Ω назовем ω–множеством.

Система F ω–множеств называется алгеброй событий, если 1) Ω  F,  F, 2) из условий А  F, В  F, следует А В F.

Любое ω-множество из этого класса называется событием.

алгебра событий F – это класс ω-множеств, замкнутый относительно конечного числа арифметических операций.

Пример 1. F = {Ω, } - класс множеств, состоящий из двух событий, достоверного и невозможного.

Пример 2. Пусть Ω ≡ и F - множество всех прямоугольников вида [ , ) [ , ) ... [ , ),- < ., k=1,m. Включив в это множество пустое множество , получим алгебру F в .

Пусть Ω – бесконечное множество элементарных исходов. Класс F ω–множеств из Ω, удовлетворяющий условиям : 1) Ω F,  F; 2) если события , ,..., ,... принадлежат множеству F, то и событие принадлежит множеству F, называется σ–алгеброй событий.

Пример 3. Рассмотрим последовательность =[ ,1), n = 1,2,…Очевидно, что =(0,1). Это означает, что результат применения счетного числа операций сложения к множествам выводит из алгебры F в R: (0,1) F. Но по определению σ-алгебры множество (0,1) σ-алгебре F в R.

σ-алгебра F в R наряду с интервалами вида [а,b) содержит любое из семи множеств: {a}, (a,b), [a,b], (a,b], (- ,b], (- ,b), (a, ). σ-алгебру F в R называют борелевской, а ее множества – интервалы указанного выше типа – борелевскими множествами.

σ-алгебра F – это класс ω-множеств, замкнутый относительно счетного числа арифметических операций.

σ-алгебра всегда является алгеброй. Для того, чтобы алгебра F была σ - алгеброй необходимо и достаточно чтобы предел любой монотонной последовательности множеств из алгебры F принадлежал этой алгебре F.

Последовательность { } называется монотонной, если n 1 или . Тогда событие A= в первом случае и A= во втором называют пределом соответствующей последовательности.

Измеримое пространство обозначают символом (Ω, F). где Ω - пространство элемнтар. исходов эксперимента, σ-алгебра F выделяет класс событий – все ω-множества из Ω, не входящие в F.

2.Непрерывные случайные величины – основные определения. Основные свойства плотности распределения.

Функция , такая что (предполагается, что интеграл сходится). называются плотностью распределения случайной величины .

Непрерывной случайной величиной называется случайная величина, функция распределения которой F(x) представима в виде интеграла .

На практике функция плотности распределения является непрерывной почти всюду на области определения, потому почти всюду справедливо равенство

Для непрерывных случайных величин плотность распределения – основная характеристика случайной величины, она определяет закон распределения случайной величины.

Свойства плотности распределения:

1. . что функция распределения F(x) – неубывающая функция.

2. По определению

3. .

3. Характеристическая функция нормально распределённой скалярной случайной величины.

Характеристической функцией с. величины называется функция:

Некоторые свойства характеристических функций

1.

так как

2. Характеристическая функция g(u) – равномерно непрерывная функция по u .

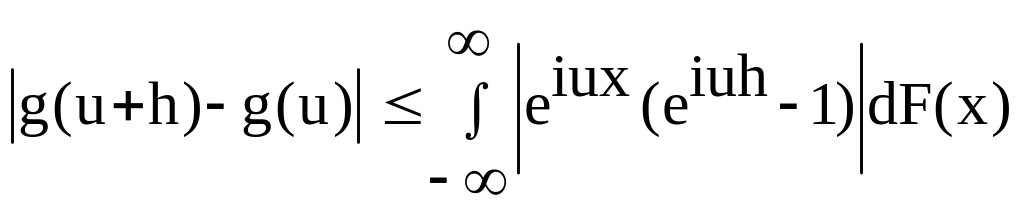
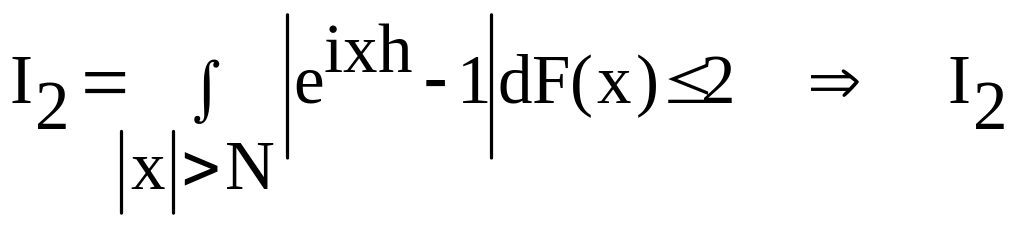-сходится Функция на отрезке [-N, N] равномерно непрерывна по h

Окончательно,

Так как не зависит от ε, то это доказывает равномерную непрерывность функции g(u).

3. .

4. Характеристическая функция является функцией действительного переменного тогда и только тогда, когда распределение F симметрично (то есть ).

5. Если существует абсолютный начальный момент порядка N, то характеристическая функция с. величины дифференцируема N раз, при этом

Так как то равномерно по u сходится, значит, его можно дифференцировать:

Если k=1, то g (u)=

6. Если существует и конечна , то .

Тогда, согласно свойству 5, существуют моменты всех порядков до N=2n включительно и .

7. Для того чтобы с. величины ξ и η была независимы, необходимо и достаточно чтобы характеристическая функция суммы этих с. величин была равна произведению их характеристических функций.

8. Если  = a +b, то

Билет3

1. Классическая вероятность событий. Свойства вероятности, вытекающие из классического определения.

Ω – дискретное множество. Все исходы равновозможные - ни один из исходов опыта не имеет никаких преимуществ в появлении перед остальными.

А – некоторое событие

Вероятностью события А называется величина: Р(А)=

Свойства:

1. P( )=0. Для невозможного события нет благоприятных случаев, m=0;

2. P(Ω)=1 . Достоверному событию благоприятствуют все случаи, m = n;

3. 0 P(A) 1. Так как 0 m n, то 0 1;

4. P(A)=1-P( ).

5. Для несовместных событий , ,..., вероятность суммы событий равна сумме их вероятностей: .

2. Экспоненциальное распределение: определение, обозначение. Производящая функция распределения, её использование для вычисления числовых характеристик.

– параметр распределения

Экспоненциально распределенная случайная величина обладает свойством - отсутствием последствия.

если непрерывная случайная величина обладает этим свойством, то вероятность попадания в любой интервал длины не зависит от того, где на числовой прямой расположено начало интервала, эта вероятность зависит только от длины интервала.

Производящей функцией для дискретно распределенной с. величины ξ называется функция .

свойства производящих функций:

1. Если производящие функции двух с. величин совпадают, то совпадают и распределения этих с. величин.

2. .

3. Если ξ и η – независимые с. величины, то производящая функция произведения этих с. величин равна произведению производящих функций сомножителей.

Ценность производящих функций заключается в связях производных этой функции с математическими ожиданиями и дисперсиями с. величин- свойство 2. Так как , то

3. Дискретная двумерная с. Величина, её описание. Формулы согласованности.

Двумерная случайная величина будет дискретной, если каждая из случайных величин дискретна. Её задают ее рядом распределения:

где - все возможные значения случайных величин . событие , за - событие , то события попарно несовместны при всех i, j . Формулы называются формулами согласованности для дискретных с. величин.

Билет4

1. Аксиоматическое определение вероятности. Аксиомы непрерывности.

Задано измеримое пространство (Ω, F). Ω – пространство э. событий, F – некоторая σ-алгебра событий (множества из F считаются событиями и только они).

Вероятностью события А из σ-алгебры F называется вещественная функция, определенная на F и удовлетворяющая следующим свойствам (аксиомам):

А1. - аксиома неотрицательности;

А2. - аксиома нормированности;

А3. Если последовательность событий такова, что то - аддитивность сложения.

Вероятность, заданную на σ-алгебре F, называют вероятностной мерой.

А3’: если события несовместны, то ;

А4: Пусть последовательность событий такова, что , , и .Тогда - аксиома непрерывности.

А4’: пусть последовательность событий такова, что , , . Тогда .

2. Равномерное распределение: определение, обозначение. Характеристическая функция распределения, её использование для вычисления числовых характеристик.

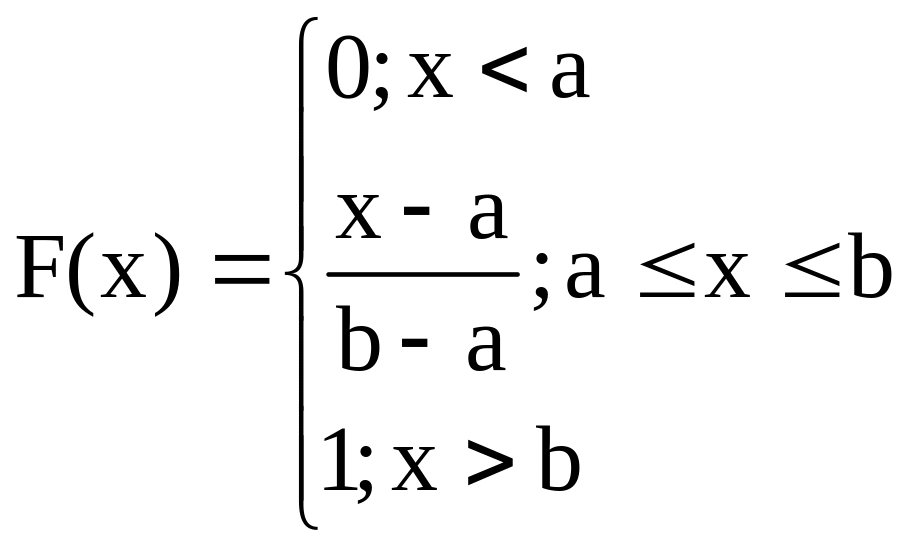
Вероятность попадания случайной величины на интервал равна , она пропорциональна длине этого интервала. Таким образом, равномерное распределение реализует принцип геометрической вероятности при бросании точки на отрезок .

Производящей функцией для дискретно распределенной с. величины ξ называется функция .

свойства производящих функций:

1. Если производящие функции двух с. величин совпадают, то совпадают и распределения этих с. величин.

2. .

3. Если ξ и η – независимые с. величины, то производящая функция произведения этих с. величин равна произведению производящих функций сомножителей.

Ценность производящих функций заключается в связях производных этой функции с математическими ожиданиями и дисперсиями с. величин- свойство 2. Так как , то

3.Условное распределение для двух непрерывных св. Условные функции распределения и плотности распределения.

и назовем условной функцией распределения предел этой условной вероятности при :

(3.12)

Как показано в [7] такой предел всегда существует, но в определенном смысле: он является производной Радона-Никодима одной меры относительно другой.

Поскольку событие есть объединение непересекающихся событий и , тогда Итак,

(3.13)

Так как:

(3.14)

Следовательно,

(3.15)

Функция имеет производную по x , т.е. существует условная плотность распределения случайной величины при условии

(3.16)

С использованием свойства 4 плотностей распределения и опустив в левой части у функции индекс получим:

(3.17)

Аналогичным рассуждением может быть получена формула:

(3.18)

Формулу (3.16) можно переписать в виде:

(3.19)

которая напоминает формулу умножения вероятностей для случайных событий.

Билет5

1. Условная вероятность Показать, что условная вероятность удовлетворяет аксиомам вероятности. Формула умножения вероятностей.

Вероятность события А при условии, что в опыте произошло событие В, называют условной вероятностью.

– вероятностное пространство. Если , , то число называют условной вероятностью события А при условии В.

При фиксированном событии , Р(А/В) является функцией событий .

1) - следует из определения. 2) , так как . 3) Пусть последовательность попарно несовместных событий. Тогда .

Если исходная вероятностная мера задана на измеримом пространстве , то условная вероятностная мера задана на измеримом пространстве , где - σ-алгебра ω-множеств вида , .