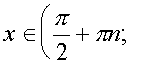Показательные уравнения. Методы решения.

Показательным уравнением называется уравнение, в котором неизвестное входит только в показатели степеней при некоторых постоянных основаниях.

Методы решения показательных уравнений:

Метод №1. Приведение обеих частей уравнения к одному основанию.

Метод №2. Замена неизвестного( применяется в том случае, если левая и правая части уравнений - многочлены).

Метод №3. Логарифмирование по удобному условию обеих частей уравнения применяется, если левая и правая части одночлены, принимающие только положительные значения при любых значениях х.

3. Показательные неравенства.

Показательным неравенством называется неравенство, в котором неизвестное входит только в показатели степеней при некоторых постоянных основаниях.

4. Методы решения показательных неравенств.

Методы решения показательных неравенств:

Метод №1. Приведение обеих частей неравенства к одному основанию.

Метод №2. Замена неизвестного( применяется в том случае, если левая и правая части неравенств- многочлены).

Метод №3. Логарифмирование по удобному условию обеих частей неравенства применяется, если левая и правая части одночлены, принимающие только положительные значения при любых значениях х.

5. Логарифм с произвольным основанием. Основные свойства логарифмов.

Логарифм- это показатель степени в которую надо ввести основание, чтобы получить логарифмируемое число.

Логарифмом положительного числа b по основанию а ( где а>1, а≠1) называется показатель степени, в которую надо возвести число а, чтобы получить число b.

Основные свойства логарифмов:

• log_a bc= log_a│b│+ log_a│c│, (a>0, a≠1, b≠0, c≠0);

• log_ab/c= log_a│b│- log_a│c│, (a>0, a≠1, b≠0, c≠0);

• log_ab^r= r log_ab, (a>0, a≠1, b>0, r- действительное число);

• loga^kb=1/k log_ab (a>0, a≠1, b>0, k≠0);

• Формула перехода к другому основанию:

log_ab=log_cb/ log_ca , в частности, log_ab=1/ log_ba, а>0, a≠1, b>0, c>0, c≠1.

6. Формула перехода к новому основанию логарифма. Десятичные и натуральные логарифмы.

• - десятичный логарифм (логарифм по основанию 10):

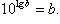
• - натуральный логарифм (логарифм по основанию e):

7. Логарифмическая функция. Её график и свойства.

Функция вида y=log_ax, где а- положительное число, а≠1, называется логарифмической функцией.

Логарифмическая функция является обратной функцией для показательной y=a^x, а>0, а≠1.

Свойства логарифмической функции

1. Область определения: (0;+∞).

2. Функция принимает значения: (-∞;+∞).

3. Если а>1, то функция является возрастающей, а если 0<a<1, то функция является убывающей.

Так как графики двух взаимообратных функций симметричны относительно прямой у=х, то это выполнимо для логарифмической показательной функцией.

8. Логарифмические уравнения. Методы решения.

Логарифмическим уравнением называется уравнение, в котором неизвестное находится под знаком логарифмической функции.

Методы решения логарифмических уравнений:

Метод №1. Метод, основанный на определении логарифма.

Метод №2. Решение с помощью потенцирования.

Метод №3. Введение нового неизвестного.

Метод №4. Переход к логарифму по новому основанию.

9. Логарифмические неравенства. Методы решения.

Простейшими логарифмическими неравенствами являются неравенства вида:

logax>b, logax<b, где a и b - некоторые действительные числа (a>0,a/=1).

Методы решения логарифмических неравенств:

Метод №1. Метод, основанный на определении логарифма.

Метод №2. Решение с помощью потенцирования.

Метод №3. Введение нового неизвестного.

Метод №4. Переход к логарифму по новому основанию.

10. Определение тригонометрических функций.

11. Основные тригонометрические тождества.

1) tg a = sin a /cos a

2) sin² a + cos² a = 1

3) 1 + tg² a = 1/cos² a

4) 1 + 1/tg² a = 1/sin² a

5) sin(90^o– a ) = cos a

6) cos(90^o– a ) = sin a

12. Формулы сложения.

13. Формулы приведения тригонометрических функций.

14. Тригонометрические функции двойного и половинного угла. Формулы понижения степени.

Формулы двойного угла:

Формулы половинного угла:

Cos ² (α/2) = (1 + cos α)/2

Sin ² (α/2) = (1 – cos α)/2

Tg ² (α/2) = (1 – cos α)/(1 + cos α)

Ctg ² (α/2) = (1 + cos α)/(1 – cos α)

tg α/2 = sin α/(1 + cos α)

cos α = (1 – tg2α/2)/(1 + tg2α/2)

sin α = (2 tg α/2)/(1 + tg2α/2)

tg α/2 = (1 – cos α)/(sin α)

ctg α = (1 – tg2α/2)/(2 tg α/2)

tg α = (2 tg α/2)/(1 – tg2α/2)

Формулы понижения степени:

15. Преобразование суммы и разности тригонометрических функций в произведение.

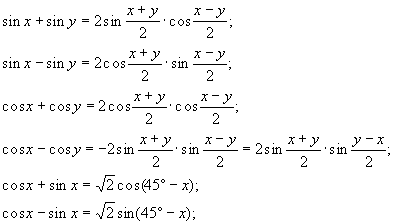
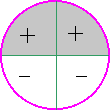
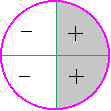
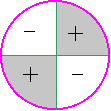
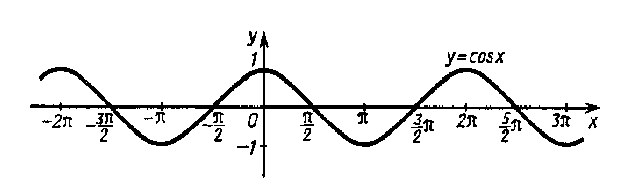
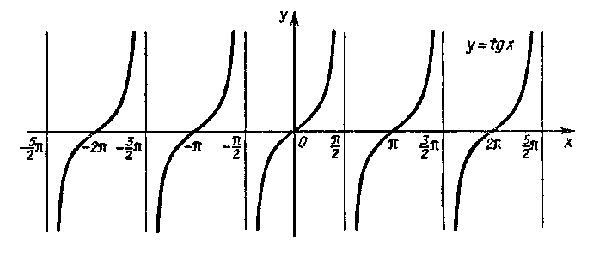
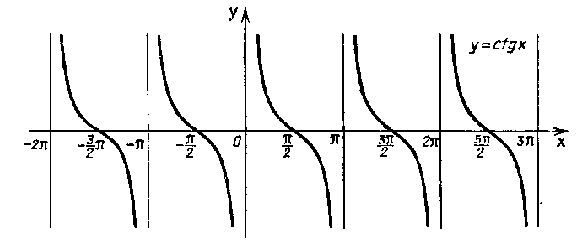
16. Тригонометрические функции. Свойства и графики.

Функции:

17. Обратные тригонометрические функции.

Функция y=arcsin x

Арксинусом числа m называется такой угол x, , для которого sinx=m,

arcsin 0=0^o

arcsin ( 1)= 90^o=

arcsin ( )= 30^o=

arcsin ( )= 45^o=

arcsin( )= 60^o=

Функция y=arccosx

Арккосинусом числа m называется такой угол x, , для которого cosx=m,

arccos 0=90^o=

arccos 1=0^o

arccos =60^o

arccos =45^o=

arccos =30^o=

arccos (-1)=180^o=

arccos ( )= 180^o-60^o=120^o=

arccos ( )=180^o-45^o=135^o=

Функция y=arctgx

Арктангенсом числа т называется такой угол х, , для которого tgx=m

arctg 0=0^o

arctg 1=

arctg =

arctg =

arctg (-1)=

arctg ( )=

arctg ( )=

Функция y=arcctgx

Арккотангенсом числа т называется такой угол х, , для которого сtgx=m

arcctg 0=

arcctg 1=

arcctg =

arcctg =

arcctg (-1)= =

arcctg ( )= =

arcctg ( )= - =

18. Простейшие тригонометрические уравнения.

К простейшим тригонометрическим уравнениям относятся следующие:

где x – неизвестная величина, a – постоянная (известное число).

Формулы решений простейших тригонометрических уравнений:

Обращаем внимание на то, что уравнения для tg x и ctg x имеют решения при любом значении a R, а уравнения для sin x и cos x – лишь при a [–1, 1].

19. Методы решения тригонометрических уравнений.

I Приведение к простейшим тригонометрическим уравнениям.

Схема решения.

1). Выразить тригонометрическую функцию через известные компоненты.

2). Найти аргумент функции по формулам:

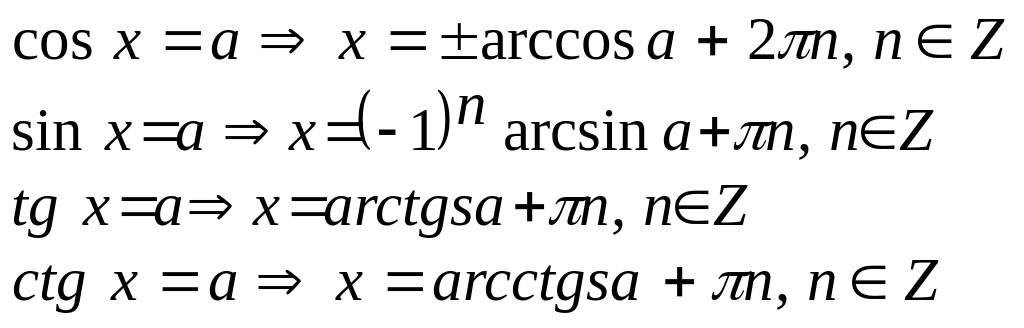
3). Найти неизвестную переменную.

Пример.

Решение.

1). ;

2). ;

3).

Ответ: .

II Замена переменной

Схема решения.

1). Привести уравнение к алгебраическому относительно одной из тригонометрических функций.

2). Обозначить полученную функцию переменной t

(ели необходимо, ввести ограничения на t)

3). Записать и решить полученное алгебраическое уравнение.

4). Сделать обратную замену.

5). Решить простейшее тригонометрическое уравнение.

Пример.

Решение.

1).

;

2). Пусть .

3). ;

4).

5).

Ответ:

III Метод понижения порядка уравнения.

Схема решения.

1). Заменить данное уравнение линейным, используя формулы понижения степени:

2). Решить полученное уравнение с помощью методов I и II.

Пример.

Решение.

1).

2).

Ответ:

IV Однородные уравнения.

Схема решения.

1) Привести уравнение к виду

или

2). Разделить обе части

уравнения на

^а) и получить уравнение относительно :

3). Решить уравнение известными способами.

Пример.

Решение.

1).

2).

3). Пусть , тогда

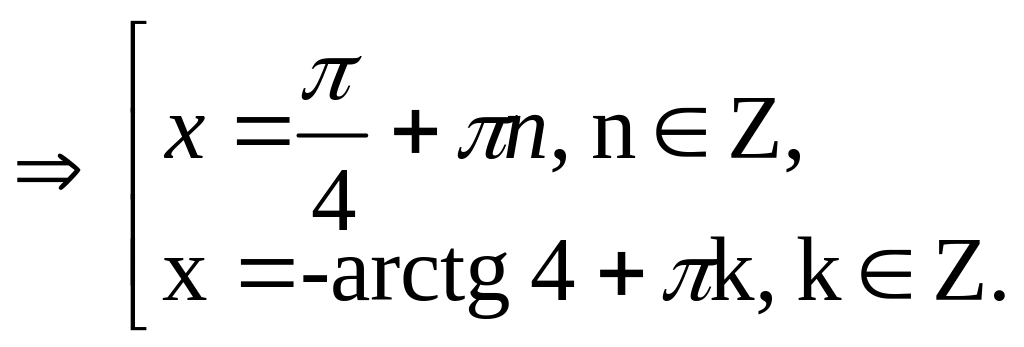
Ответ:

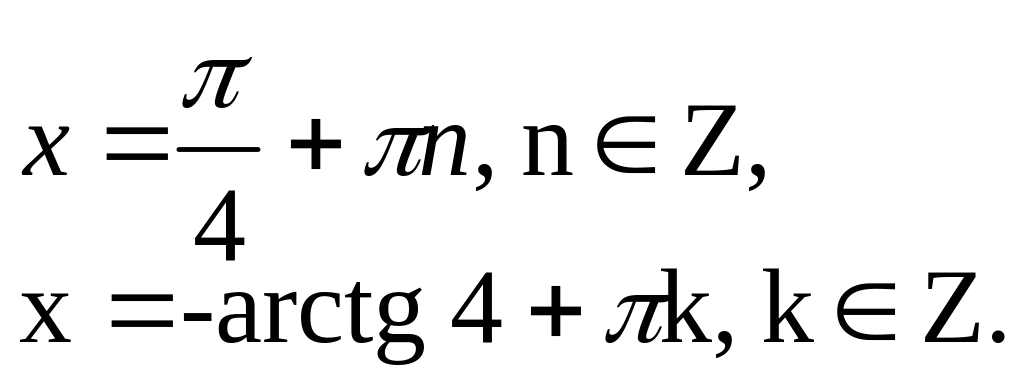
V Метод преобразования уравнения с помощью тригонометрических формул.

Схема решения.

1). Используя тригонометрические формулы, привести уравнение к уравнению, решаемому методами I,II,III,IV.

2). Решить полученное уравнение известными методами.

Пример.

Решение.

1). ;

2). ;

Ответ:

20. Простейшие тригонометрические неравенства.

sin x≥a или sin x≤a;

cos x≥a или cos x≤a;

tg x≥b или tg x≤b;

ctg x≥b или ctg x≤b; │a│≤1; b € R;

21. Предел функции. Теоремы о пределах.

22. Раскрытие неопределенностей при вычислении пределов.

    1. Разложить на множители

    2. Умножение на сопряженное

23. Вычисление 1 и 2 замечательных пределов.

24. Непрерывность функции. Точки разрыва. Свойства непрерывных функций.

Функция F(x)-непрерывна в данной точке x(o), если ее предел в точке х(о) существ., и равен значению функции в этой точке

Lim F(x)= F(x₀)

x→x₀

Свойства: Если функции F₁(x) и F₂(x) непрерывны в точке А:

1. их сумма, разность и произведение есть функция непрерывная.

2. Частное. F₁(x)/F₂(x) есть непрерывная функция при условии F₂(х)≠0

Функция F(x)- непрерывна на отрезке, если она непрерывна в каждой точке этого отрезка.

Если в каких либо точках интервала, функция не является непрерывной, то такие точки называют ТОЧКАМИ РАЗРЫВА.

25. Производная функции и ее применение.

Производной функции в точке х₀ называется предел отношения приращения функции к вызвавшему его приращению аргумента при стремлении х к х₀. Производная функции в точке х₀ обозначается символом .

Производная функции и сама является функцией - она определяется значением в точке . Эта функция обозначается символом или .

26. Задачи, производящие к понятию производной.

27. Определение производной.

Производная— функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции.

28. Геометрический и механический смысл производной.

Механический смысл производной

Пусть материальная точка движется прямолинейно и - длина пути, проходимого за время t , отсчитываемого от некоторого момента времени t₀ .

Для определения скорости V в данный момент t придадим переменной t некоторое приращение , при этом приращение пути будет равно .

Отношение называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени t , и обозначается

Предел называется величиной мгновенной скорости движения в момент времени t .

Таким образом, мгновенная скорость в момент времени t прямолинейного движения, совершаемого по закону равна значению производной .

29. Производная суммы, произведения, частного, степени.

30. Сложная функция. Её производная.

Сложная функция- пусть у является функцией переменной u, а переменная u в свою очередь является функцией от x y=F(u), u=µ(x). Тогда функция у = F(µ(x)) называется сложной функцией.

Сложная функция, если область определения F содержит множество значений µ.

u- называется промежуточной переменной.

31. Производная показательной и логарифмической функции.

32. Производные тригонометрических функций.

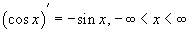
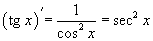
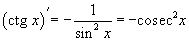
33. Производные обратных тригонометрических функций.

II семестр

1. Признаки возрастания и убывания функции. Теорема Лагранжа.

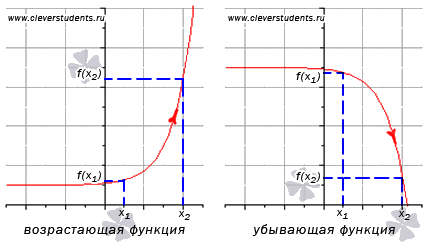
Определение возрастающей функции.

Функция y = f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Определение убывающей функции.

Функция y = f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

Теорема Лагранжа: Воспользуемся геометрическим смыслом производной, чтобы дать наглядные пояснения справедливости того, что существует касательная к графику f в точке с абсциссой с из интервала (а; b), параллельная секущей, проходящей через точки A (a; f (а)), В (b; f (b)).

Рассмотрим прямую l, параллельную АВ и не имеющую общих точек с частью графика, соответствующей промежутку [а; b]. Будем перемещать эту прямую l по направлению к графику f так, чтобы она оставалась параллельной АВ. Зафиксируем положение l₀ этой прямой в момент, когда у нее появятся общие точки с этой частью графика.

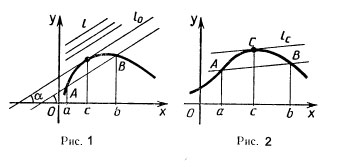Из рис.1 видно, что любая из таких «первых» общих точек — точка касания прямой l₀ с графиком f. Обозначим абсциссу этой точки через с. Тогда f’(c)=tg α, где α — угол между прямой l₀ и осью абсцисс. Но l||АВ, поэтому угол α равен углу наклона секущей АВ, т. е. Итак, если функция дифференцируема, то на интервале (а; b) найдется такая точка c∈ (а; b) (рис. 2), что

2. Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I.

Достаточные признаки возрастания и убывания функции:

• если функция f(x)в каждой точке интервала (a,b) имеет положительную производную, то сама функция в этом интервале возрастает;

• если функция f(x) в каждой точке интервала (a,b) имеет отрицательную производную, то функция в этом интервале убывает.

Определение. Функция у=f(x) имеет экстремум (максимум или минимум) в точке х=х₀, если f(x₀) является наибольшим или наименьшим значением функции в некоторой окрестности этой точки.

3. Экстремумы функции. Исследование функции на экстремумы по 1 производной.

Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство f(x₁) < f (x₂) (f(x₁) > f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ¢(x) > 0 (f ¢(x) < 0).

Точка x₀ называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x₀, для всех точек которой верно неравенство f(x) £ f(x₀) (f(x) ³ f(x₀)).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f ¢(x₀) = 0, либо f ¢(x₀) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

По 1-ой производной:

Пусть x₀ - критическая точка. Если f ¢ (x) при переходе через точку x₀ меняет знак плюс на минус, то в точке x₀ функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x₀ экстремума нет.

Необходимые условия экстремума. Если точка x₀ является точкой экстремума функции f(x), то либо f ¢(x₀) = 0, либо f ¢(x₀) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

4. Выпуклость графика функции. Точки перегиба.

Выпуклость функции, точки перегиба

Хорда, соединяющая точки M₁(x₁, f(x₁)), M₂(x₂, f(x₂)) графика функции f(x) задается функцией

y=L(x, x₁, x₂ ) = f(x₁) + f(x₂) (*)

Это проверяется подстановкой координат x₁, x₂ в правую часть.

Определение. Функция f(x) называется выпуклой вверх на [a,b], если для "x₁<x<x₂ из [a,b]

L(x, x₁, x₂ ) = f(x₁)

Если f непрерывна на [a,b], дважды дифференцируема на (a,b) и f¢¢(x)>0 на (a,b), то f строго выпукла вниз.

Доказательство. "a£x₁<x<x₂£b имеем f(x) - L(x, x1, x2 )=f(x) -

Определение. Точка x₀ называется точкой перегиба функции f, если в точке x₀ существует касательная и в некоторой окрестности точки x₀ график f лежит по разные стороны от касательной.

5. Наибольшее и наименьшее значение на отрезке.

Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.

Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:

1.Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.

2.Вычислить значения функции на концах отрезка при x = a, x = b.

3.Из всех полученных значений выбрать наибольшее и наименьшее.

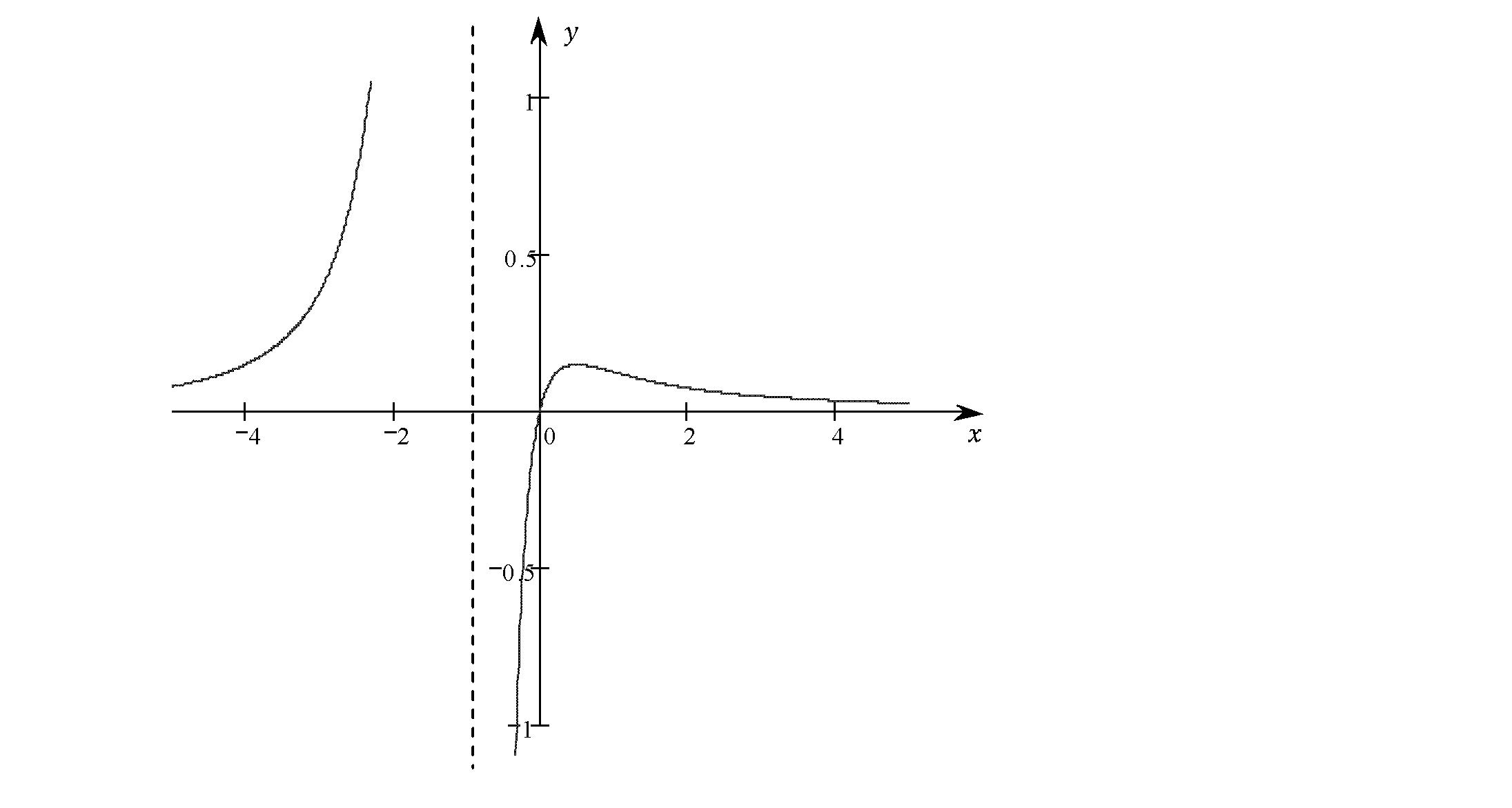
6. Исследование функции и построение графика.

1 a.Найти ОДЗ и точки разрыва функции.

b.Найти точки пересечения графика функции с осями координат.

2.Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.

3.Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

4.Найти асимптоты графика функции: а) вертикальные, b) наклонные.

5.На основании проведенного исследования построить график функции.

7. Первообразная. Неопределенный интеграл, его свойства.

Определение. Функция F (x) называется первообразной для функции f (x) на данном промежутке, если для любого х из данного промежутка F'(x)= f (x).

Пример:

1.Выяснить, является ли функция F (x) = х 3 – 3х + 1 первообразной для функции f(x) = 3(х 2 – 1).

Решение: F'(x) = (х 3 – 3х + 1)′ = 3х 2 – 3 = 3(х 2 – 1) = f(x), т.е. F'(x) = f(x), следовательно, F(x)является первообразной для функции f(x).

Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом .

Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.

Свойства неопределённого интеграла, непосредственно следующие из определения:

1. 

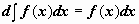
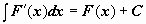2. или

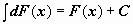
8. О 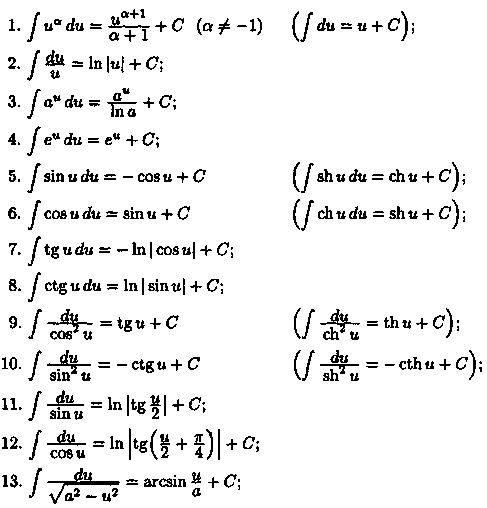сновные табличные интегралы.

9. Интегрирование способом подстановки. Интегралы вида

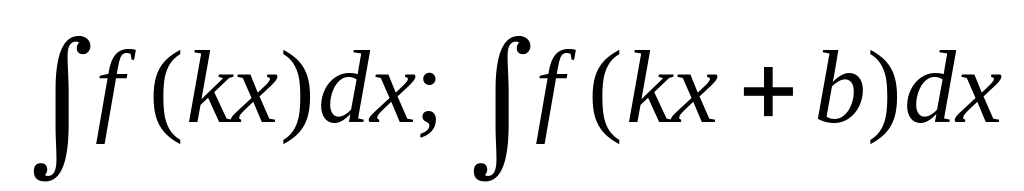
10. Определенный интеграл. Геометрический смысл.

Е сли f(x) непрерывна и положительна на [a, b], то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x).

11. Вычисление определенного интеграла способом подстановки.

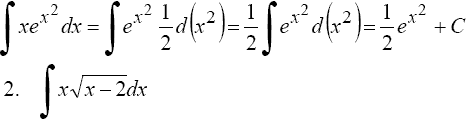
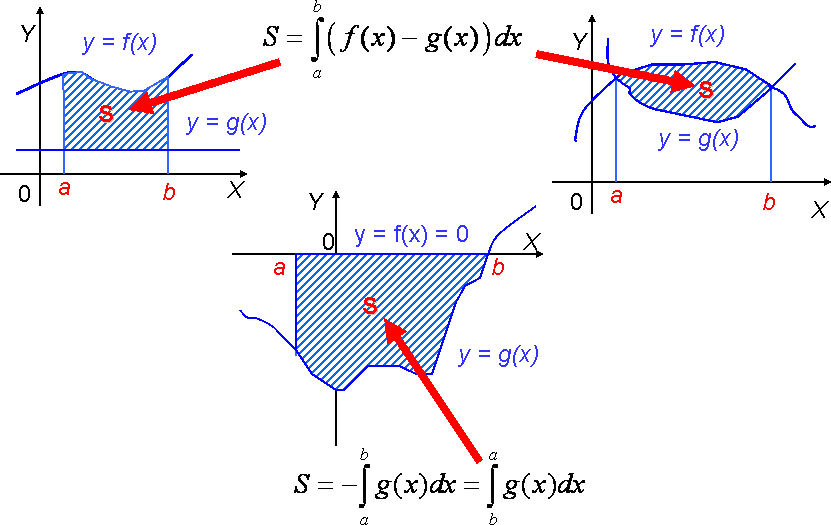
12. Вычисление площадей плоских фигур через определенный интеграл.

Примеры плоских фигур

13. Применение интегралов для решения физических задач.

14. Векторы в координатах. Деление отрезка в данном отношении.

15. Уравнение прямой: каноническое, параметрическое, через две точки.

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

Уравнение прямой, проходящей через две заданные несовпадающие точки

Уравнение прямой, проходящей через две заданные несовпадающие точки и

или в общем виде

Параметрические уравнения прямой.

Параметрические уравнения прямой могут быть записаны в виде:

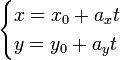где t — производный параметр, ax, ay — координаты x и y направляющего вектора прямой, при этом

Каноническое уравнение прямой

Каноническое уравнение получается из параметрических уравнений делением одного уравнения на другое:

где — координаты Х и Y направляющего вектора прямой, и координаты точки, принадлежащей прямой.

16. Уравнение прямой с нормальным вектором. Общее уравнение прямой. Частные случаи.

Общее уравнение

Ax + By + C ( > 0).

Вектор = (А; В) - нормальный вектор прямой.

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

17. Уравнение прямой в отрезках, с угловым коэффициентом, уравнение пучка прямых.

;

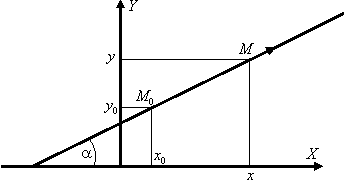
18. В заимное расположение прямых. Условие параллельности и перпендикулярности прямых на плоскости.

Условие параллельности прямых: k₁ = k₂. Условие перпендикулярности прямых: k₁·k₂ = −1.

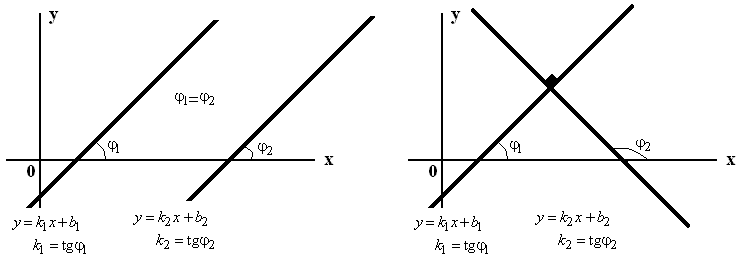
19. Угол между прямыми.

Углом между пересекающимися прямыми на плоскости, называется градусная мера наименьшего из углов, образованных при пересечении этих прямых. Угол между совпадающими или параллельными прямыми считается равным нулю.

Угол α между двумя прямыми, заданными уравнениями: y=k1x+b1 (первая прямая) и y=k2x+b2 (вторая прямая), может быть вычислен по формуле (угол отсчитывается от 1й прямой ко 2й против часовой стрелки):

tg(α)=(k2-k1)/(1+k1k2)

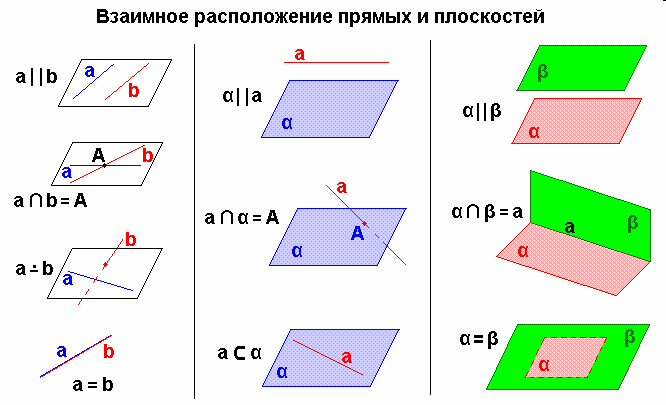
20. Аксиомы стереометрии. Признак параллельности прямой и плоскости. Признак Параллельности двух плоскостей.

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.

С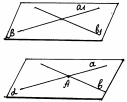 лучаи взаимного расположения прямой и плоскости:

а) прямая лежит в плоскости;

б) прямая и плоскость имеют только одну общую точку;

в) прямая и плоскость не имеют ни одной общей точки.

Определение. Две плоскости называются параллельными, если они не имеют общих точек.

Параллельность плоскостей и обозначается так: || . Рассмотрим признак параллельности двух плоскостей.

Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Свойства параллельных плоскостей:

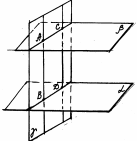Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.

21. Признак перпендикулярности прямой и плоскости.

Признаки параллельности прямой и плоскости:

1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.

2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.

Признаки параллельности плоскостей:

1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.

Признаки перпендикулярности прямой и плоскости:

1) Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.

2) Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

Наклонная к плоскости. Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости.

Теорема о трёх перпендикулярах. Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной.

Признаки параллельности прямых в пространстве:

1) Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.

2) Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей.

Признак перпендикулярности плоскостей: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Теорема об общем перпендикуляре к двум скрещивающимся прямым. Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр.

22. П ерпендикуляр и наклонные к плоскости. Теорема о трех перпендикулярах.

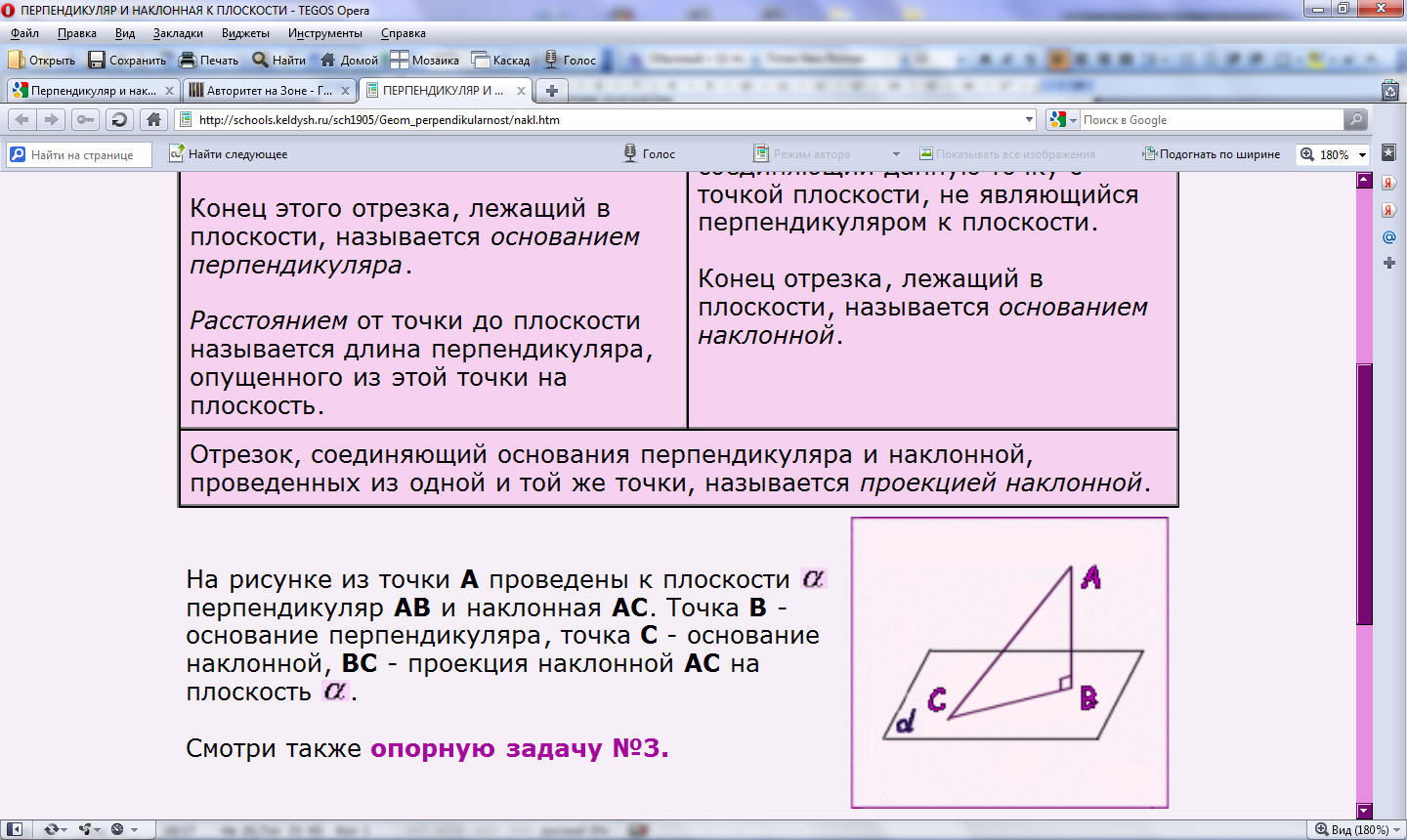
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ.

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.

И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

23. Двугранный угол. Признак перпендикулярности двух плоскостей.

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Полуплоскости называются гранями, а ограничивающая их прямая --- ребром двугранного угла.

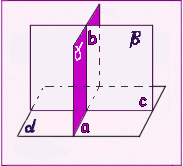
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ.

Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

24. Призма. Виды призм. Площадь поверхности.

Призма — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.

Виды призм:

Прямая призма — призма, у которой все боковые ребра перпендикулярны основанию, в противном случае призма называется наклонной.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или высоту).

В прямой призме боковые ребра являются высотами.

Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.

Объем наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.

Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания.

Основания правильной призмы являются правильными многоугольниками.

Боковые грани правильной призмы являются равными прямоугольниками.

Боковые ребра правильной призмы равны.

Правильная призма является прямой.

Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.

Площадь боковой поверхности произвольной призмы , где P — периметр перпендикулярного сечения, l — длина бокового ребра.

25. Пирамида. Виды пирамид. Сечение пирамиды. Площадь поверхности пирамиды.

П ирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.

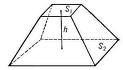
26. Усеченная пирамида. Площадь ее поверхности.

Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию.

27. Объем призмы. Объем параллелепипеда. Решение задач.

Объем призмы: V = S_основ • H

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту: V= SH= abc

28. Объем пирамиды. Объем усеченной пирамиды. Решение задач.

Объем пирамиды равен одной трети произведения площади основания на высоту: где S – площадь основания, H – высота пирамиды.

Объем V усеченной пирамиды может быть найден по формуле где H – высота усеченной пирамиды, S1 и S2 – площади ее оснований.

29. Цилиндр. Сечение цилиндра. Площадь поверхности.

Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей).

Сечение цилиндра плоскостью, параллельной его оси, представляет прямоугольник.

Осевым сечением называется сечение, которое проходит через ось цилиндра.

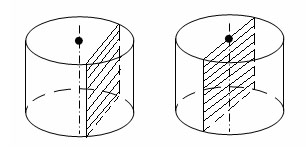
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту: S=2π rh

Полная площадь поверхности цилиндра:

S= 2π r(h+ r)

Сечение цилиндра.

30. К онус (рис. 1.19). Усеченный конус. Площадь поверхности конуса и усеченного конуса.

Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

Площадь конуса:

Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.

Площадь поверхности усеченного конуса:

S=π(r12+(r1+ r2) l+ r22)

31. Шар, сфера. Площадь сферы.

Шар — это тело ограниченное шаровой поверхностью.

Сфера (греч. σφαῖρα — шар) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы.

Площадь сферы:

Площадь сферической части поверхности шарового сектора: , где H – высота сегмента.

32. Объем цилиндра.

Ц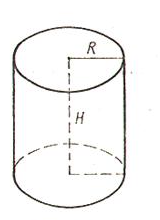 или́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Объем:

33. Объем конуса и усеченного конуса.

Конус: Усеченный конус: V=1/3π h(r²+r₁·r₂+r₂²)

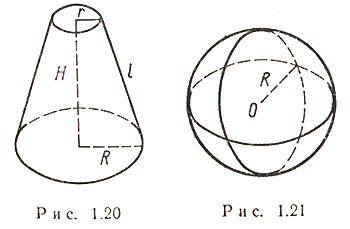
Усеченный конус (рис. 1.20)

34. Объем шара и его частей.

Объем:

Объем шарового сегмента:

Объем шарового сектора:

35. Параллелепипед. Виды и свойства.

П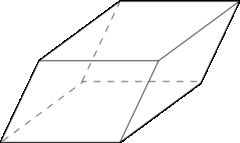 араллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.

Свойства:

• Параллелепипед симметричен относительно середины его диагонали.

• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

• Противолежащие грани параллелепипеда параллельны и равны.

• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.