
- •Г.В. Соколовська с.Ю. Соколовський Вступ до аналізу. Диференціальне числення функцій однієї та кількох змінних.
- •Тема 1. Границя числової послідовності
- •Тема 2. Границя та неперервність функції в точці
- •Тема 3. Точки розриву функції
- •Тема 3. Похідна та деякі її застосування
- •Тема 5. Дослідження функції
- •Тема 6. Частинні похідні функції кількох змінних та деякі їх застосування
- •Тема 7. Екстремум функції двох змінних.
Тема 7. Екстремум функції двох змінних.
Завдання
7.1
Дослідити на екстремум функцію
![]() .
.
Розв’язання
Застосуємо схему дослідження функції на екстремум:
1) знайдемо
частинні похідні
![]() і
і
![]() ;
;
2) знайдемо
критичні точки (тобто точки, в яких
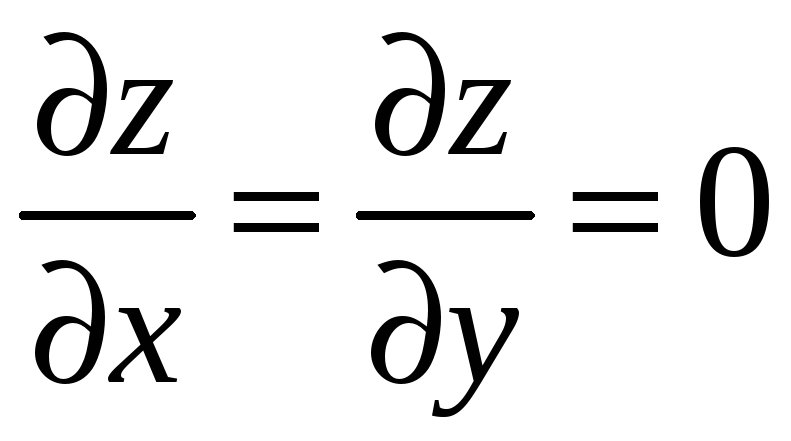 або не існує хоча б одна з них);
або не існує хоча б одна з них);
3) знайдемо
частинні похідні другого порядку
 і складемо функцію двох змінних
і складемо функцію двох змінних
 ;
;
4)
перевіримо виконання достатньої умови
екстремуму в кожній з критичних точок,
а саме, якщо в критичній точці
![]() ,
то вона є точкою екстремуму, якщо
,
то вона є точкою екстремуму, якщо
![]() ,
то це не точка екстремуму;
,
то це не точка екстремуму;
5) в
точках екстремуму знайдемо значення
![]() (якщо
(якщо
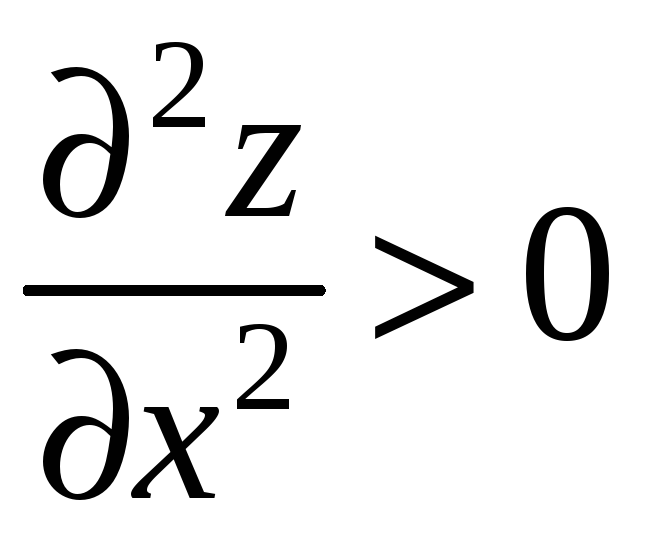 ,
то це точка мінімуму, якщо
,
то це точка мінімуму, якщо
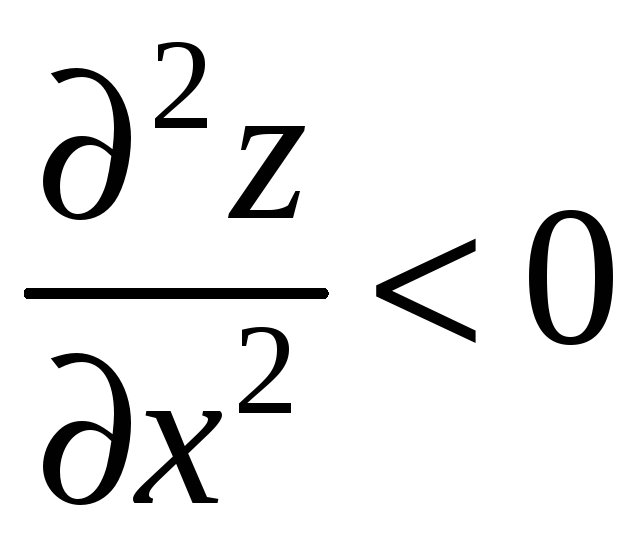 - точка максимуму).
- точка максимуму).
1)
![]() ;
;
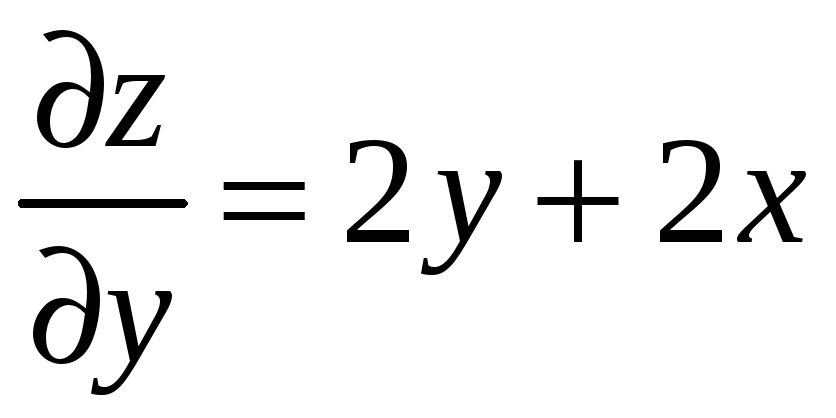 .
.
2) Оскільки
частинні похідні визначені при будь-яких
значеннях
![]() і
і
![]() ,
то критичними точками є розв’язки
системи рівнянь
,
то критичними точками є розв’язки
системи рівнянь
![]() .
Розв’язавши її одержимо:
.
Розв’язавши її одержимо:
![]() - критичні точки.
- критичні точки.
3)
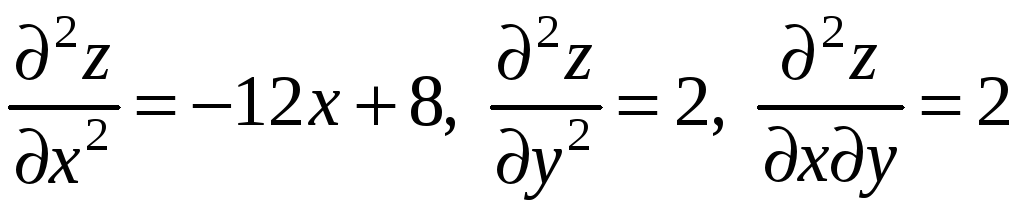 .
.
![]() .
.
4)
![]() ,
отже
,
отже
![]() - точка екстремуму;
- точка екстремуму;
![]() ,
отже
,
отже
![]() не є точкою екстремуму.
не є точкою екстремуму.
5)
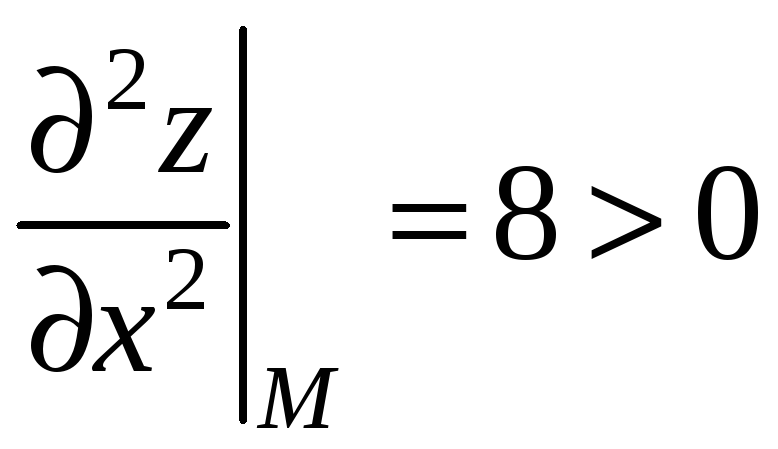 ,
тоді
,
тоді
![]() - точка мінімуму;
- точка мінімуму;
![]() .
.
Завдання
7.2
Знайти найбільше та найменше значення
функції
![]() в області
в області
![]() обмеженій лініями:
обмеженій лініями:
![]() .
.
Розв’язання
Неперервна в замкненій обмеженій області функція досягає в ній своїх найбільшого та найменшого значень. Ці значення можна знайти за схемою:
1) знайдемо
частинні похідні
![]() і
і
![]() ;
;
2) знайдемо критичні точки;
3)
обчислимо значення функції в критичних
точках, що належать області
![]() ;
;
4)
розв’яжемо задачу умовного екстремуму
на межі області
![]() ;
;
5) з отриманих в пунктах 3 і 4 значень функції виберемо найбільше та найменше.
1)
![]() ;
;
 .
.
2)
Розв’яжемо систему рівнянь
![]() .
Маємо
.
Маємо
![]() - критична точка.
- критична точка.
3)
Зобразимо область
![]() (рис.
6).
(рис.
6).
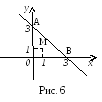
В нашому
випадку область
![]() -
це трикутник
-
це трикутник
![]() .
Як бачимо,
.
Як бачимо,
![]() .
Знайдемо
.
Знайдемо
![]() .
.
4) На
відрізку
![]() .
Після підстановки
.
Після підстановки
![]() функція
функція
![]() перетвориться на функцію однієї змінної
перетвориться на функцію однієї змінної
![]() .
Цю функцію досліджуємо на найбільше та
найменше значення на відрізку
.
Цю функцію досліджуємо на найбільше та
найменше значення на відрізку
![]() .
Маємо:
.
Маємо:
![]() ;
;
![]() ,
тоді
,
тоді
![]() -
критична точка, яка належить відрізку
-
критична точка, яка належить відрізку
![]() .
.
![]() .
Знайдемо також значення функції на
лівому кінці проміжку
.
Знайдемо також значення функції на
лівому кінці проміжку
![]() .
Зазначимо, що
.
Зазначимо, що
![]() ,
,![]() .
.
Розглянемо
відрізок
![]() .
На цьому відрізку одержимо функцію
.
На цьому відрізку одержимо функцію
![]() .
Тоді
.
Тоді
![]() - критична точка, яка належить відрізку
- критична точка, яка належить відрізку
![]() .
Знайдемо
.
Знайдемо
![]() і
і
![]() .
.
Аналогічно
досліджуємо відрізок
![]() .
На ньому маємо функцію
.
На ньому маємо функцію
![]() або
або
![]() .
Знайдемо
.
Знайдемо
![]() -
критична точка.
-
критична точка.
![]() ,
тому знаходимо
,
тому знаходимо
![]() .
Значення
.
Значення
![]() на кінцях відрізку вже знайдені, адже
на кінцях відрізку вже знайдені, адже
![]() і
і
![]() .
.
5) Таким
чином, найбільшим в області
![]() значенням функції
значенням функції
![]() є
є
![]() ,
а найменшим -
,
а найменшим -
![]() .
.
Завдання
7.3
На площині
![]() знайти точку
знайти точку
![]() ,
сума квадратів відстаней від якої до
трьох прямих
,
сума квадратів відстаней від якої до
трьох прямих
![]() була б найменшою.
була б найменшою.
Розв’язання
Позначимо
через
![]() і
і
![]() відстані від точки
відстані від точки
![]() до прямих
до прямих
![]() ,
,
![]() і
і
![]() відповідно. Як бачимо, відстань від
точки
відповідно. Як бачимо, відстань від
точки
![]() до осі
до осі
![]()
![]() дорівнює модулю її абсциси, тобто
дорівнює модулю її абсциси, тобто
![]() .
Аналогічно знаходимо відстань від точки
.
Аналогічно знаходимо відстань від точки
![]() до осі
до осі
![]()
![]() :
:
![]() .
Для знаходження
.
Для знаходження
![]() скористаємось формулою для знаходження
відстані від точки
скористаємось формулою для знаходження
відстані від точки
![]() до прямої
до прямої
![]() ,
що має вигляд:
,
що має вигляд:
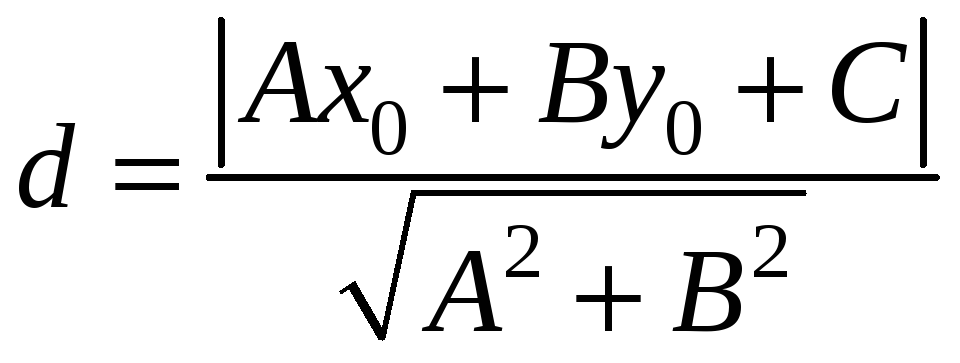 .
Отже
.
Отже
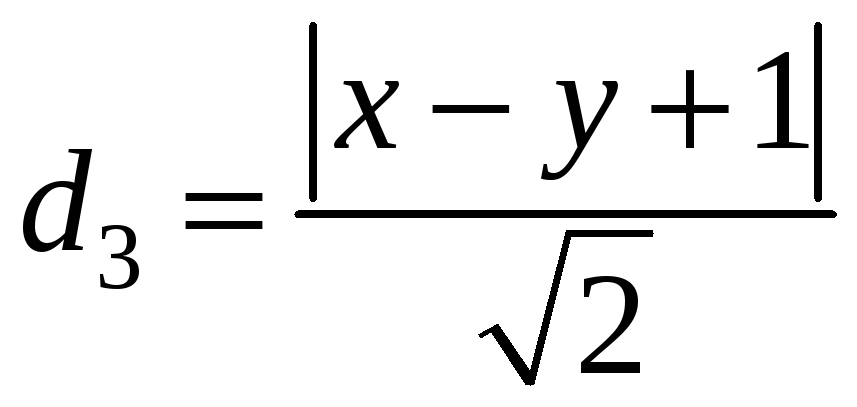 ,
тобто
,
тобто
 .
.
Таким
чином, слід знайти найменше значення
функції
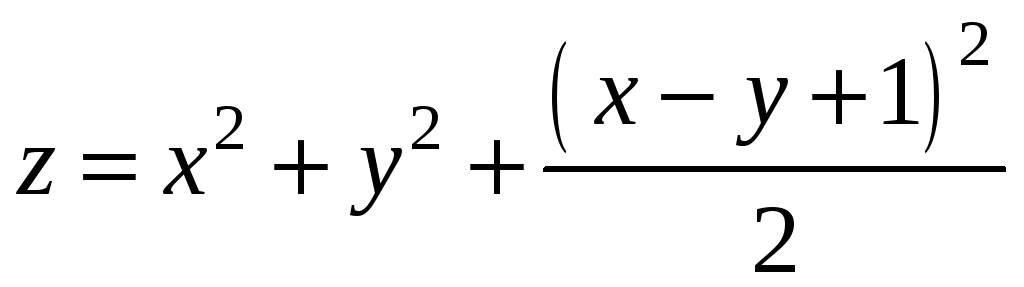 .
Знайдемо частинні похідні:
.
Знайдемо частинні похідні:
![]() ,
,
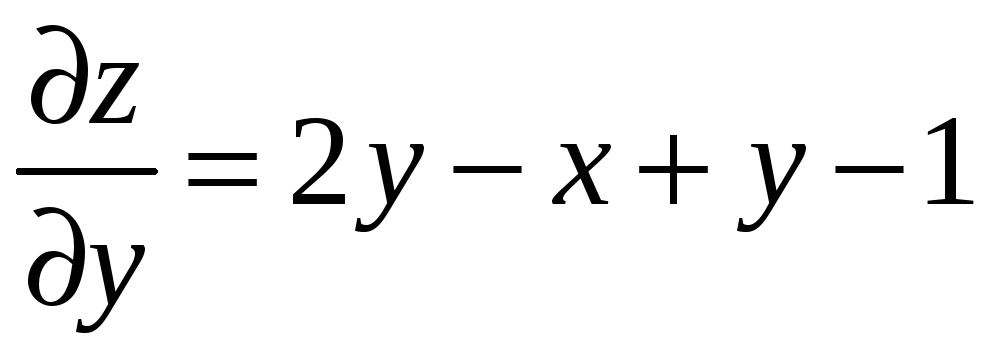 .
Розв’язавши систему
.
Розв’язавши систему
![]() ,
маємо критичну точку
,
маємо критичну точку
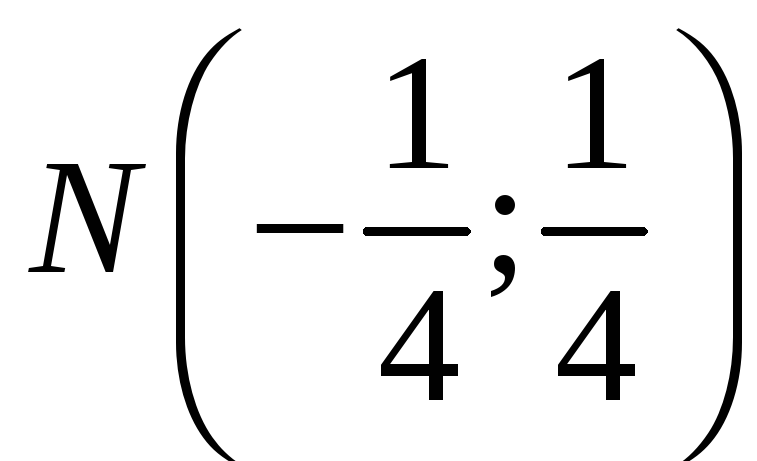 .
Дізнаємось, чи буде вона точкою екстремуму.
.
Дізнаємось, чи буде вона точкою екстремуму.
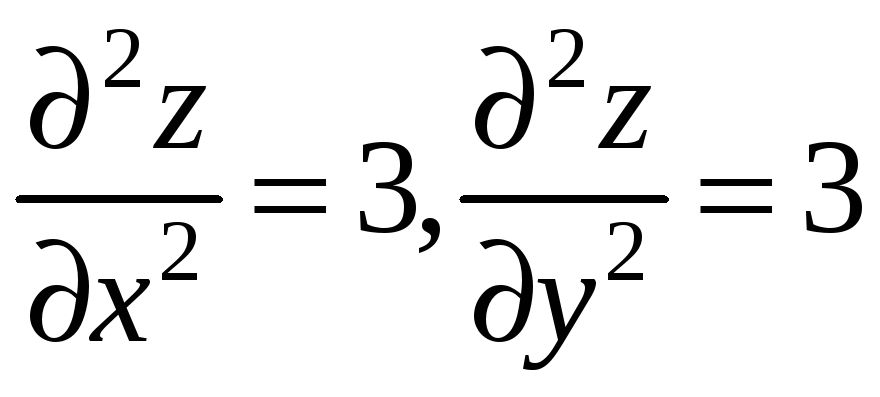 ,
,
 ;
;
![]() ;
;
![]() .
Отже
.
Отже
![]() - точка екстремуму. При цьому
- точка екстремуму. При цьому
![]() - це точка мінімуму, оскільки
- це точка мінімуму, оскільки
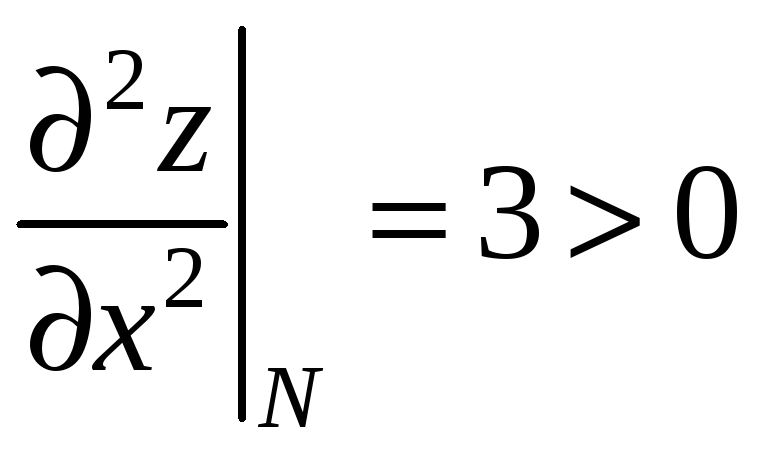 .
Отже для точки
.
Отже для точки
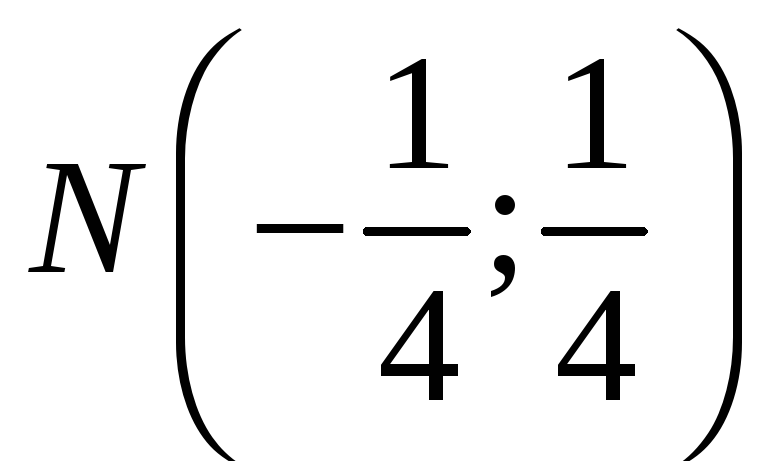 сума квадратів відстаней до трьох прямих
сума квадратів відстаней до трьох прямих
![]() ,
,
![]() ,
,
![]() є найменшою.
є найменшою.
Завдання для самостійного розв’язування
Завдання
7.4
Перевірити, чи будуть точки
![]() критичними для функції
критичними для функції
![]() .
.
Завдання
7.5
Перевірити, чи будуть точки
![]() ,
,
![]() точками екстремуму для функції
точками екстремуму для функції
![]() .
.
Завдання 7.6 Дослідити на екстремум функцію
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() .
.
Завдання
7.7
Знайти найбільше і найменше значення
функції
![]() в області
в області
![]() ,
обмеженій заданими лініями
,
обмеженій заданими лініями
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Завдання
7.8
Знайти точку трикутника
![]() сума квадратів відстаней від якої до
його вершин буде найбільшою.
сума квадратів відстаней від якої до
його вершин буде найбільшою.
Завдання
7.9
Знайти точку чотирикутника
![]()
![]() сума квадратів відстаней від якої до
його вершин є найменшою.
сума квадратів відстаней від якої до
його вершин є найменшою.
Завдання
7.10
Додатне число
![]() записати у вигляді трьох доданків
записати у вигляді трьох доданків
![]()
![]() так, щоб їх добуток був найбільшим.
так, щоб їх добуток був найбільшим.
Завдання
7.11
З усіх прямокутних паралелепіпедів
заданого об’єму
![]() знайти той, площа повної поверхні якого
є найменшою.
знайти той, площа повної поверхні якого
є найменшою.
Завдання
7.12
В кулю радіуса
![]() вписано паралелепіпед. Визначити розміри
паралелепіпеда так, щоб його об’єм був
найбільшим.
вписано паралелепіпед. Визначити розміри
паралелепіпеда так, щоб його об’єм був
найбільшим.
