
- •Г.В. Соколовська с.Ю. Соколовський Вступ до аналізу. Диференціальне числення функцій однієї та кількох змінних.
- •Тема 1. Границя числової послідовності
- •Тема 2. Границя та неперервність функції в точці
- •Тема 3. Точки розриву функції
- •Тема 3. Похідна та деякі її застосування
- •Тема 5. Дослідження функції
- •Тема 6. Частинні похідні функції кількох змінних та деякі їх застосування
- •Тема 7. Екстремум функції двох змінних.
Тема 2. Границя та неперервність функції в точці
Завдання
2.1
Довести за означенням границі функції,
що
 .
.
Розв’язання
Наведемо
означення границі функції в точці. Число
![]() називається границею функції
називається границею функції
![]() в точці
в точці
![]() ,
якщо функція визначена в деякому околі
цієї точки (крім, можливо, самої точки
,
якщо функція визначена в деякому околі
цієї точки (крім, можливо, самої точки
![]() )
і для будь-якого числа
)
і для будь-якого числа
![]() існує таке число
існує таке число
![]() (
(![]() залежить від
залежить від
![]() ),
що для всіх значень
),
що для всіх значень
![]() ,
які задовольняють нерівність
,
які задовольняють нерівність
![]() ,
виконано:
,
виконано:
![]() .
.
Задамо
як завгодно мале додатне число
![]() і знайдемо таке
і знайдемо таке
![]() ,
що при всіх
,
що при всіх
![]() ,
що задовольняють нерівність
,
що задовольняють нерівність
![]() ,
виконано:
,
виконано:
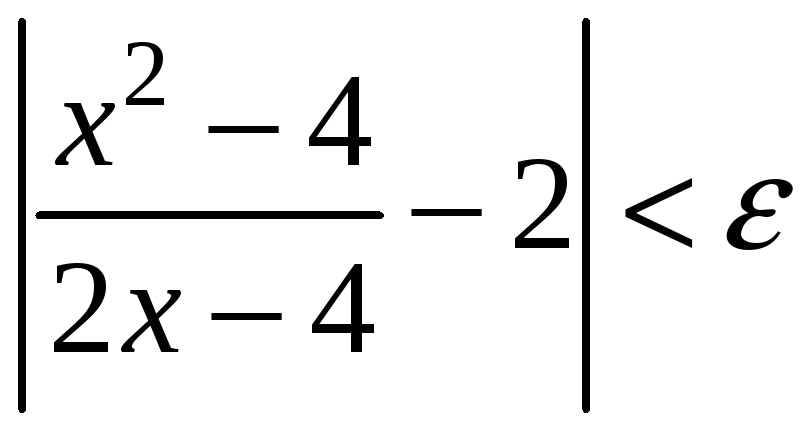 .
.
![]()
Виконаємо
перетворення останньої нерівності
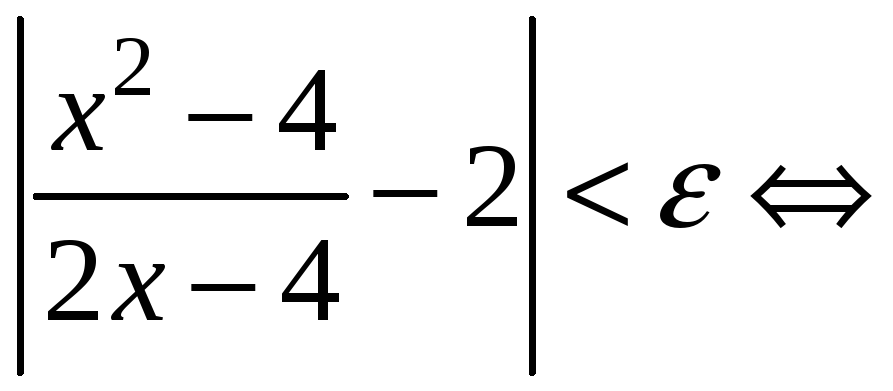
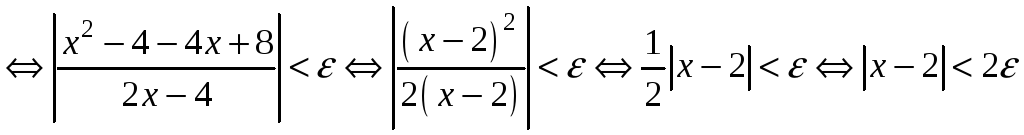 .
Таким чином, обравши
.
Таким чином, обравши
![]() ,
одержимо: при всіх
,
одержимо: при всіх
![]() ,
що задовольняють умову
,
що задовольняють умову
![]() ,
виконано нерівність
,
виконано нерівність
![]() .
Граничну рівність доведено.
.
Граничну рівність доведено.
Завдання
2.2
Довести за означенням, що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Розв’язання
Наведемо
означення функції неперервної в точці
![]() .
Функція
.
Функція
![]() називається неперервною в точці
називається неперервною в точці
![]() ,
якщо
,
якщо
1) вона визначена в цій точці і деякому її околі;
2) границя
функції
![]() в точці
в точці
![]() збігається з її значенням в цій точці:
збігається з її значенням в цій точці:
![]() .
.
Обчислимо
![]() і доведемо, що
і доведемо, що
![]() .
Задамо
.
Задамо
![]() і вимагатимемо виконання нерівності
і вимагатимемо виконання нерівності
![]() або
або
![]() .
Як бачимо, вона є справедливою при
.
Як бачимо, вона є справедливою при
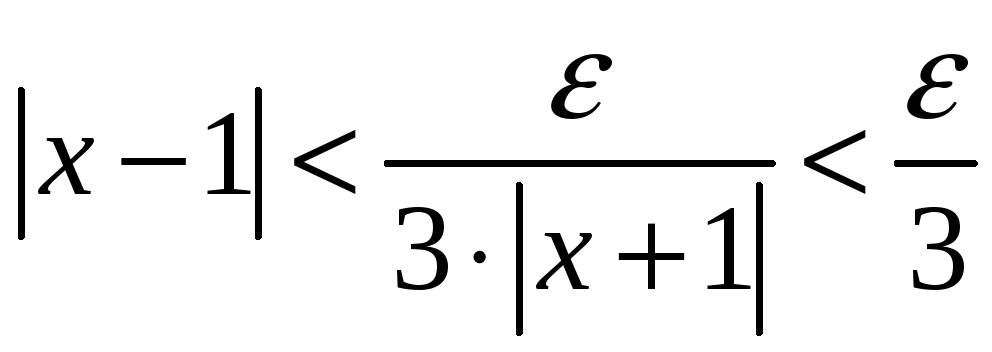 (оскільки
(оскільки
![]() ,
адже розглядається достатньо малий
окіл точки
,
адже розглядається достатньо малий
окіл точки
![]() ).
Отже знайдено таке число
).
Отже знайдено таке число
![]() ,
що для всіх
,
що для всіх
![]() ,
які задовольняють нерівність
,
які задовольняють нерівність
![]() ,
виконується:
,
виконується:
![]() .
Неперервність функції в точці
.
Неперервність функції в точці
![]() доведено.
доведено.
Завдання
2.3
Обчислити границі 1)
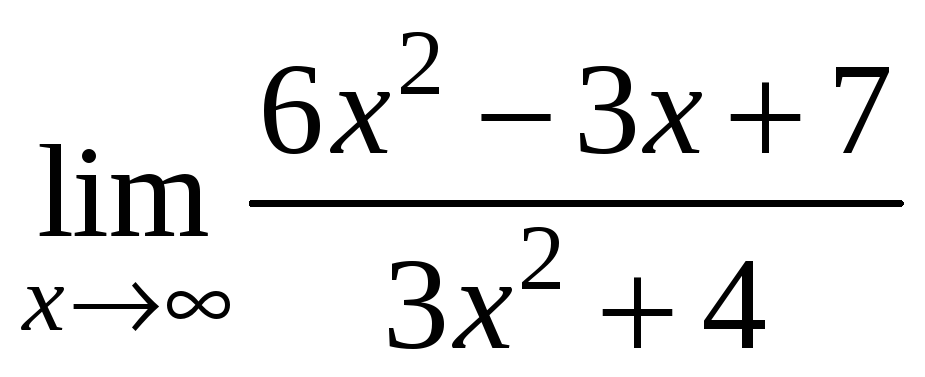 ;
;
2)
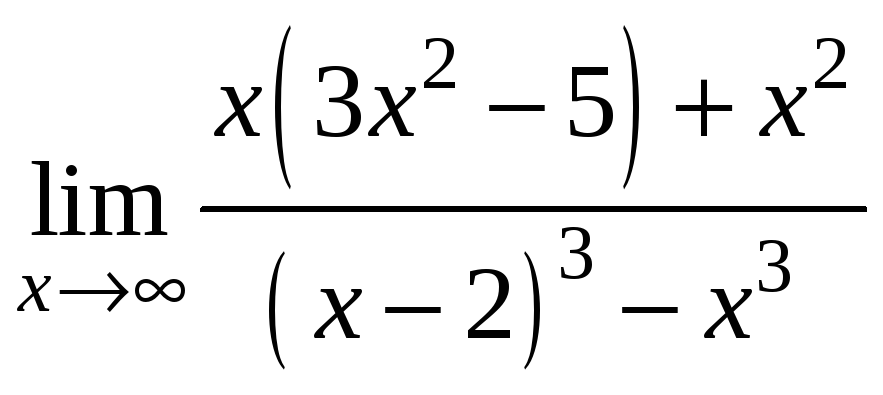 :
3)
:
3)
![]() .
.
Розв’язання
1) Можна
скористатись означенням границі функції
при
![]() (
(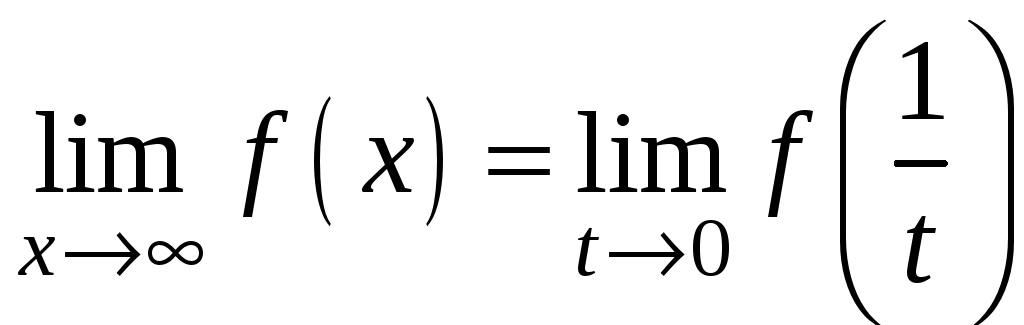 )
і теоремами про арифметичні дії над
функціями, що мають границі
)
і теоремами про арифметичні дії над
функціями, що мають границі
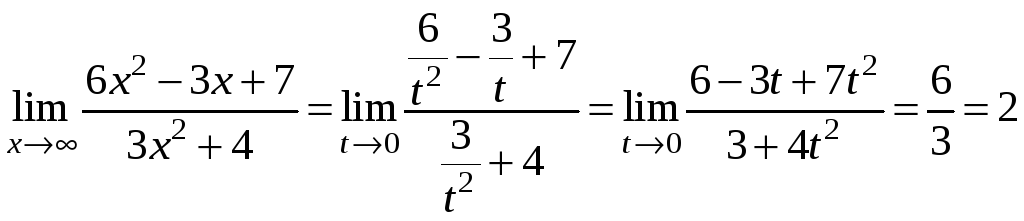 .
На практиці ж зазвичай не виконують
явно заміну
.
На практиці ж зазвичай не виконують
явно заміну
![]() ,
а ділять чисельник і знаменник на
найстарший степінь знаменника
,
а ділять чисельник і знаменник на
найстарший степінь знаменника
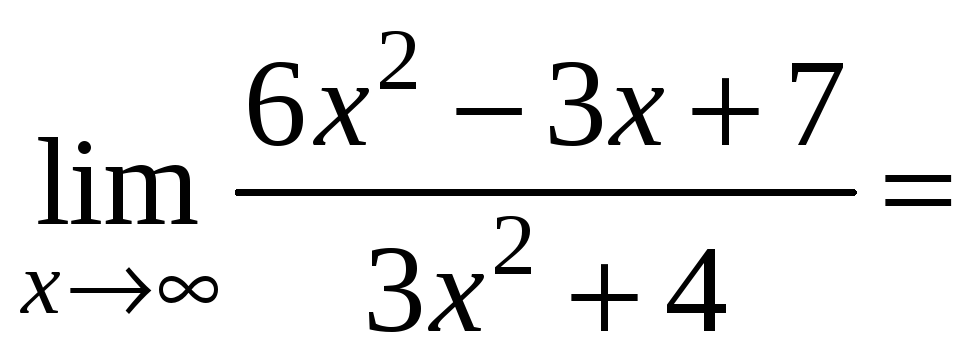
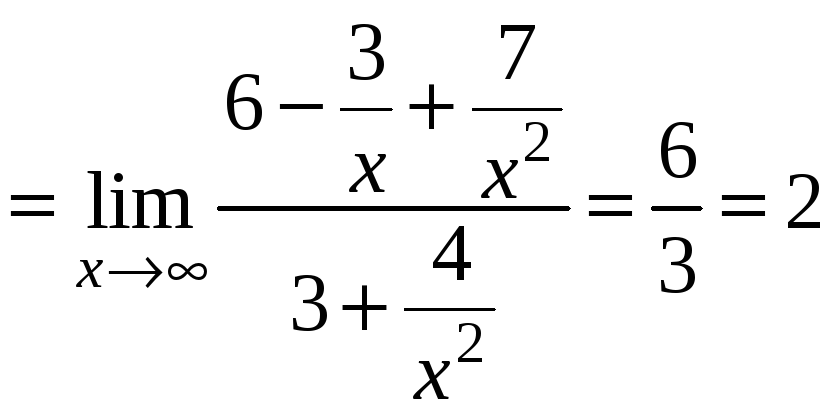 .
.
Наступні два приклади розв’язуються аналогічно.
2)
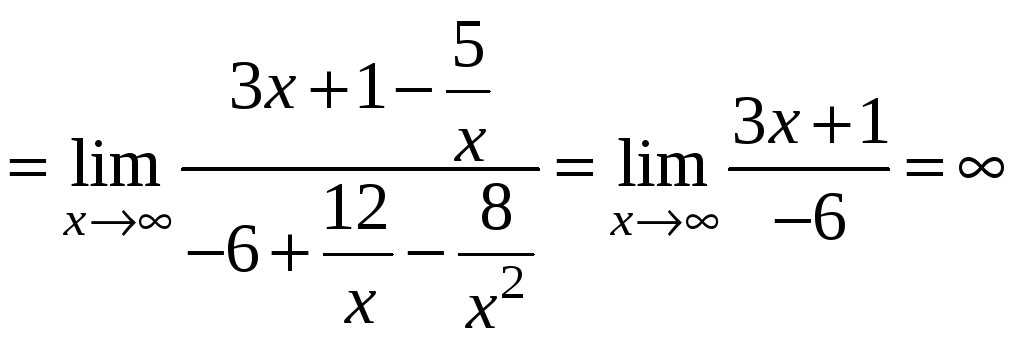 .
.
3)
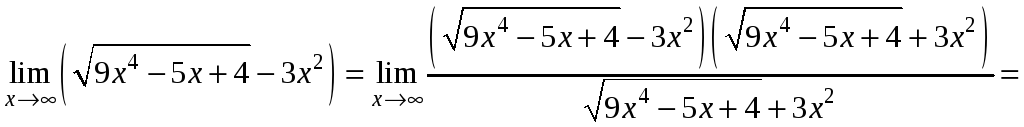
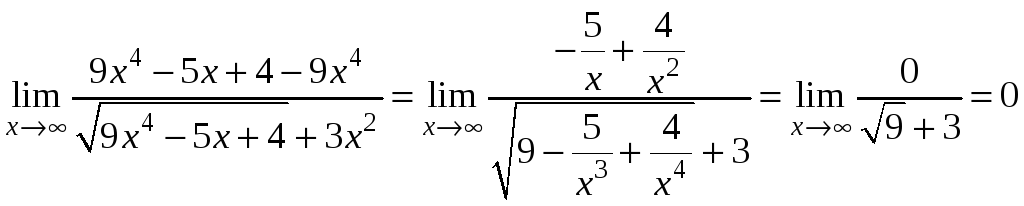 .
.
Завдання
2.4
Обчислити границі 1)
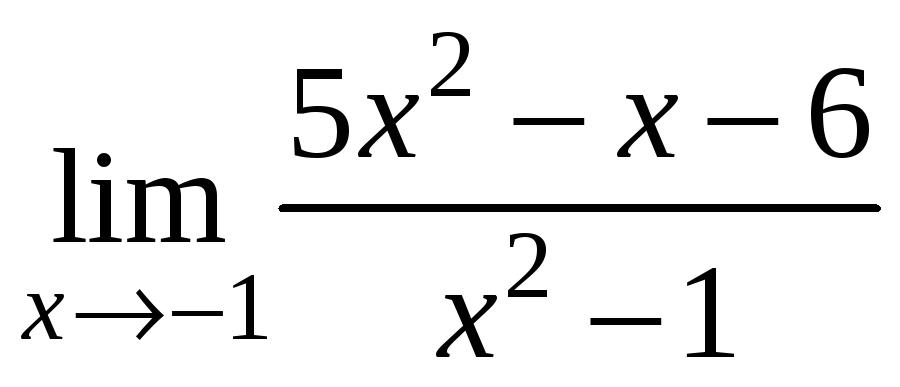 ;
;
2)
 ;
3)
;
3)
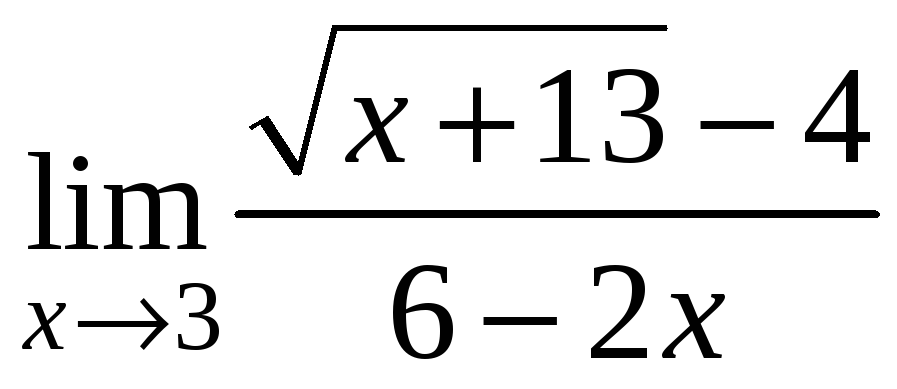 .
.
Розв’язання
1) Функція
 не визначена в точці
не визначена в точці
![]() .
Чисельник і знаменник дробу в цій точці
дорівнюють нулю. Отже має місце
невизначеність
.
Чисельник і знаменник дробу в цій точці
дорівнюють нулю. Отже має місце
невизначеність
![]() .
Розкладемо чисельник і знаменник на
множники. Знаменник – за формулою
різниці квадратів, а чисельник – за
формулою:
.
Розкладемо чисельник і знаменник на
множники. Знаменник – за формулою
різниці квадратів, а чисельник – за
формулою:
![]() ,
де
,
де
![]() -
корені квадратного рівняння
-
корені квадратного рівняння
![]() .
.
Маємо
![]()
![]() ,
,
 .
Тоді можна скоротити дріб
.
Тоді можна скоротити дріб
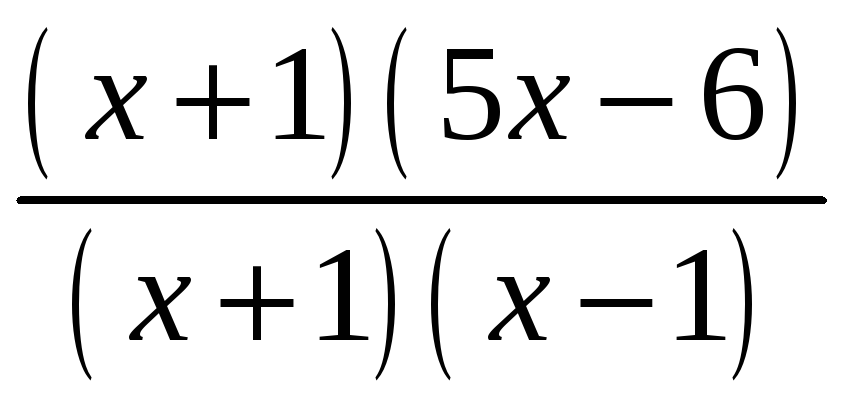 на
на
![]() в будь – якому околі точки
в будь – якому околі точки
![]() (крім самої цієї точки).
(крім самої цієї точки).
Одержимо:
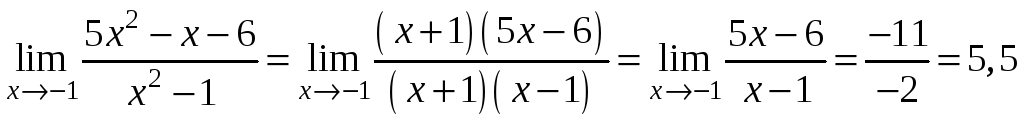 .
.
2) Для
розкриття невизначеності виду
![]() в цьому прикладі також розкладемо
чисельник і знаменник на множники.
Знаменник розкладемо за формулами
скороченого множення:
в цьому прикладі також розкладемо
чисельник і знаменник на множники.
Знаменник розкладемо за формулами
скороченого множення:
![]() . Знаючи, що в розкладанні чисельника
обов’язково присутній множник
. Знаючи, що в розкладанні чисельника
обов’язково присутній множник
![]() ,
другий множник знайдемо за допомогою
ділення
,
другий множник знайдемо за допомогою
ділення
![]() на
на
![]() .
М
.
М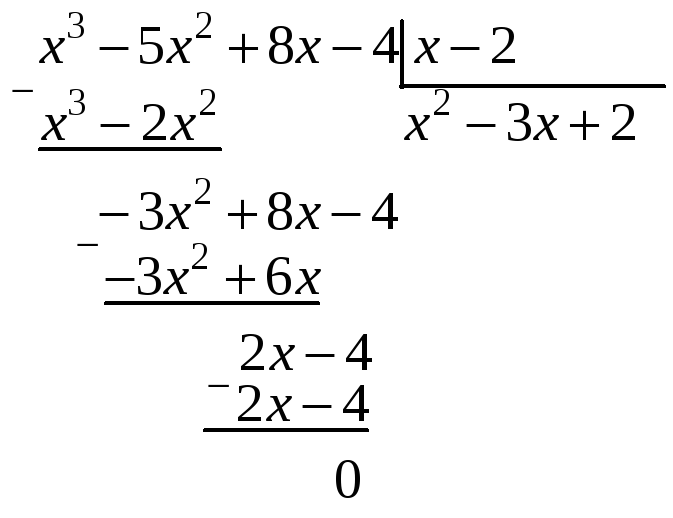 аємо:
аємо:
Тоді
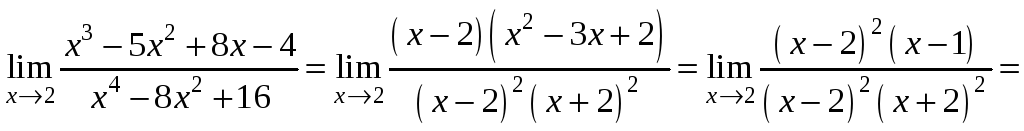
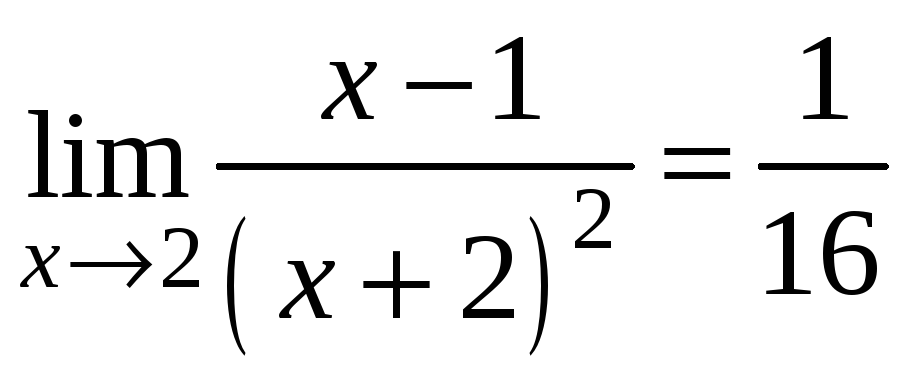 .
.
3) Тут
невизначеність виду
![]() також розкривається скороченням дробу
на
також розкривається скороченням дробу
на
![]() ,
але спочатку звільнимось від
ірраціональності в чисельнику.
,
але спочатку звільнимось від
ірраціональності в чисельнику.
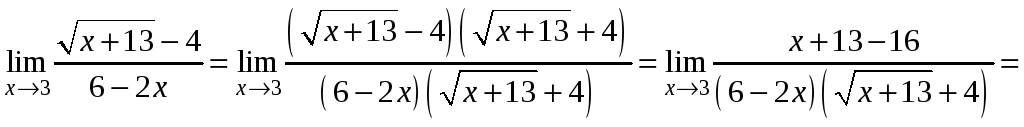
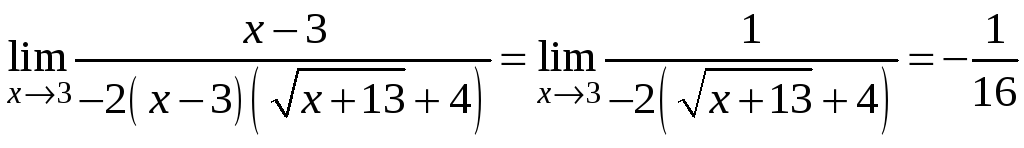 .
.
Завдання
2.5
Обчислити границі 1)
![]() ;
2)
;
2)
![]() ;
;
3)
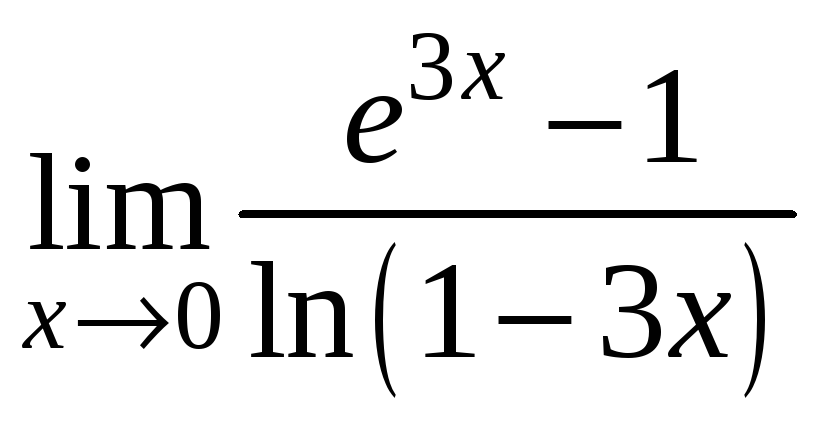 ;
4)
;
4)
 .
.
Розв’язання
У цих прикладах застосовується принцип заміни нескінченно малих функцій на еквівалентні та деякі тригонометричні формули.
1)
![]() .
Тому
.
Тому
 .
.
2)
![]() .
.
![]() .
Отже
.
Отже
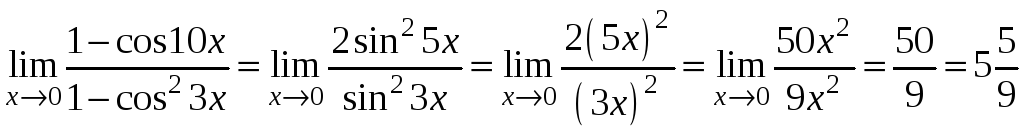 .
.
3)
![]() .
Тоді
.
Тоді
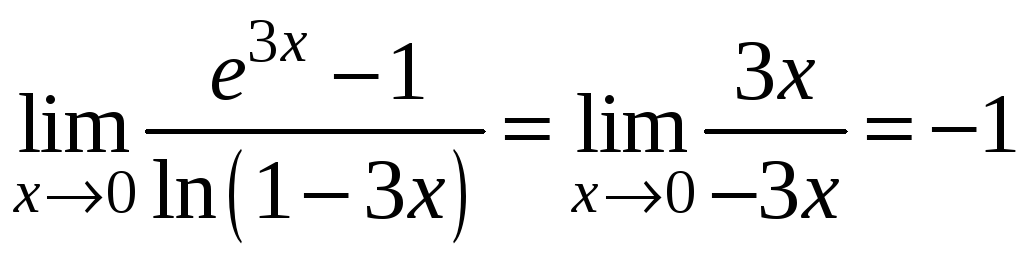 .
.
4)
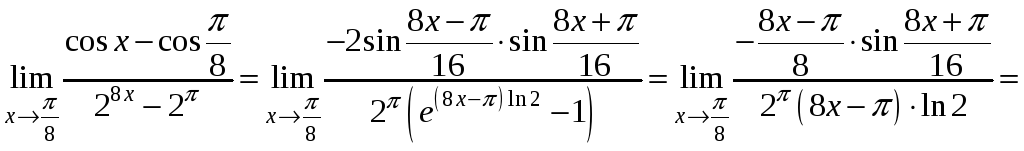
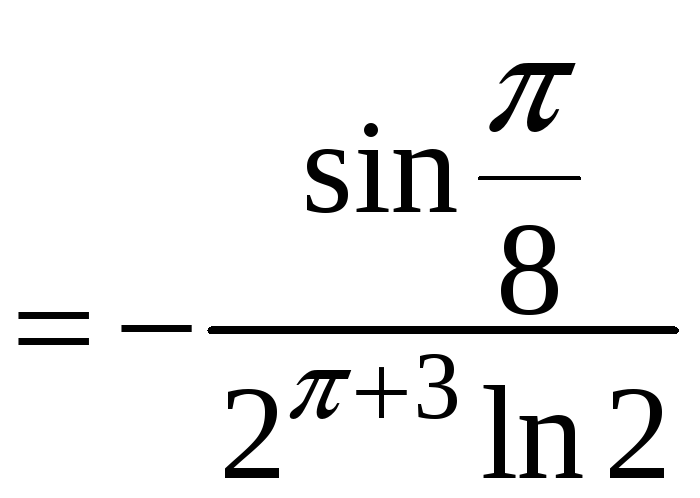 .
При розв’язуванні цього приклада було
застосовано формули
.
При розв’язуванні цього приклада було
застосовано формули
![]() ,
,
![]() ,
а також еквівалентність функцій:
,
а також еквівалентність функцій:
![]() при
при![]() .
.
Завдання 2.6 Обчислити границі
1)
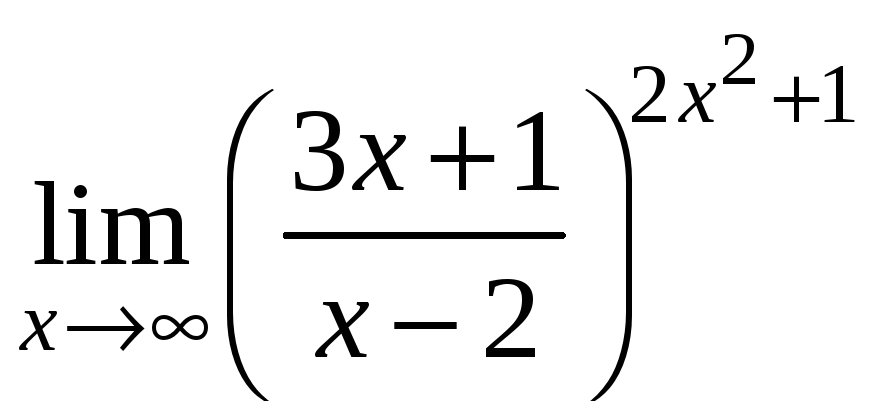 ;
2)
;
2)
 ;
3)
;
3)
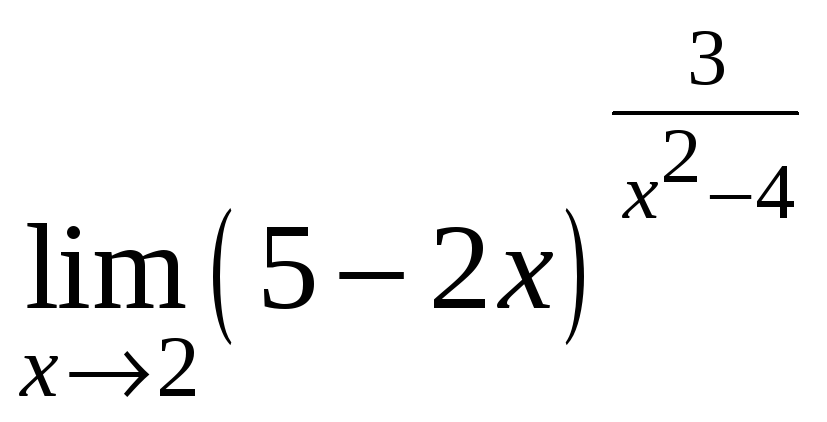 .
.
Розв’язання
1)
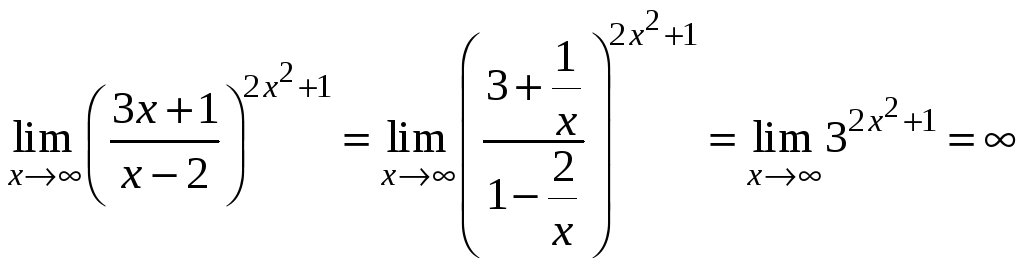 .
.
В інших
прикладах маємо невизначеність виду
![]() ,
яку розкриємо за допомогою другої
визначної границі
,
яку розкриємо за допомогою другої
визначної границі
![]() .
.
2)
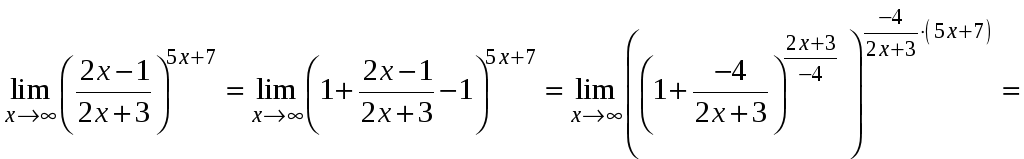
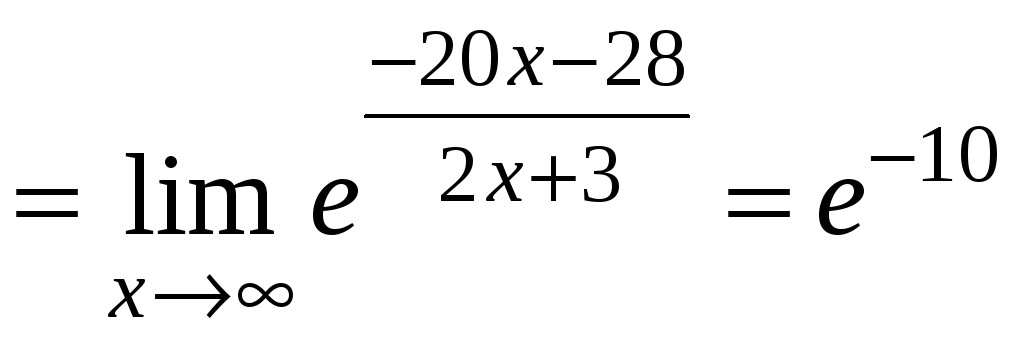 ,оскільки
,оскільки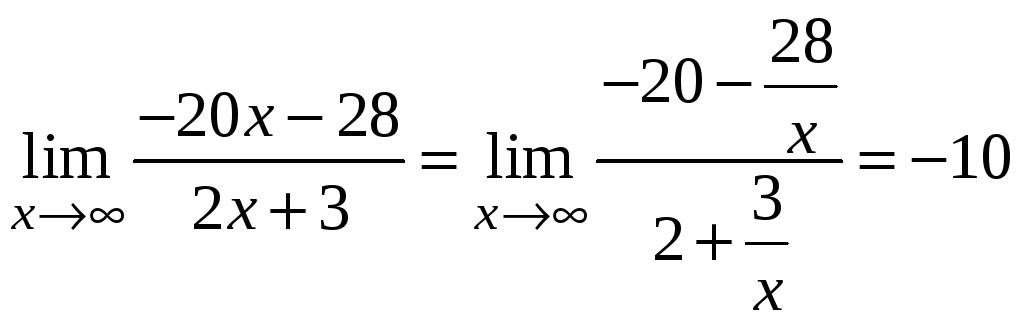
3) .
.
Завдання для самостійного розв’язування
Завдання 2.7 Обчислити границі
1)
 ;
2)
;
2)
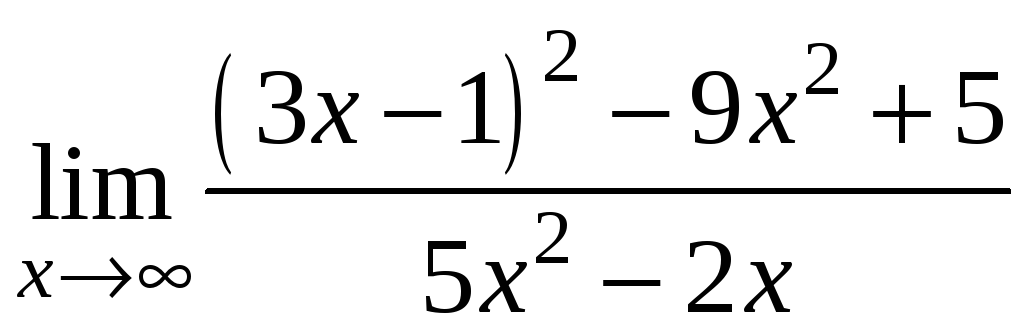 ;
3)
;
3) ;
;
4)
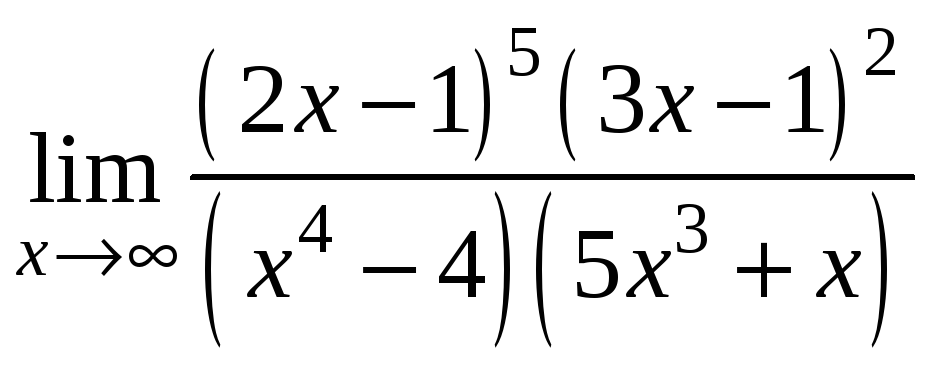 ;
5)
;
5)
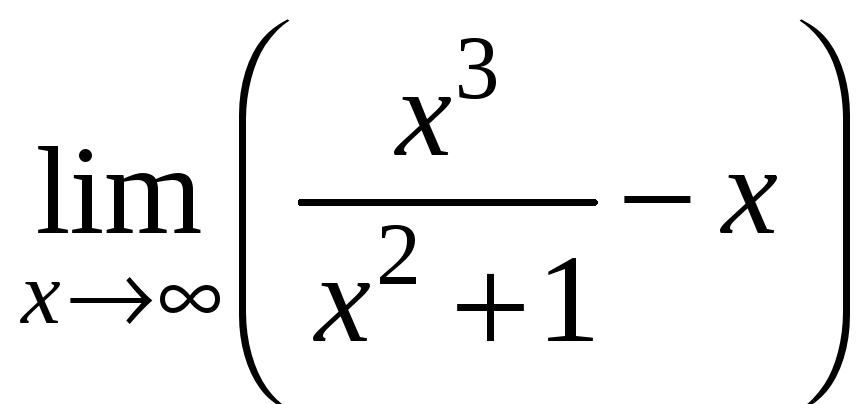 ;
6)
;
6)
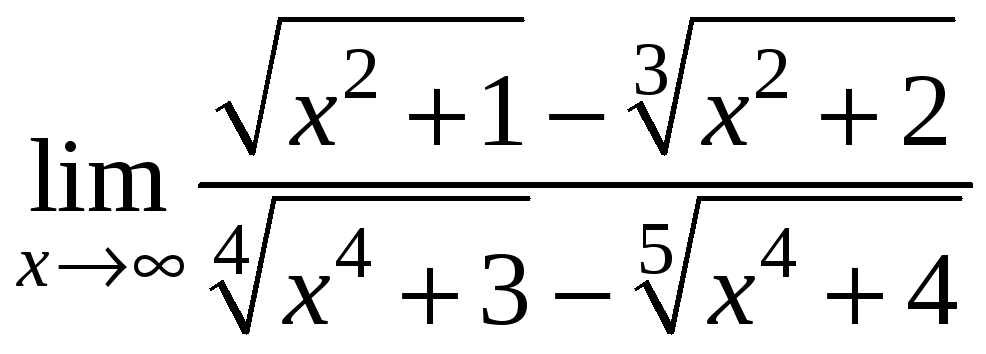 ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() .
.
Завдання 2.8 Обчислити границі
1)
![]() ;
2)
;
2)
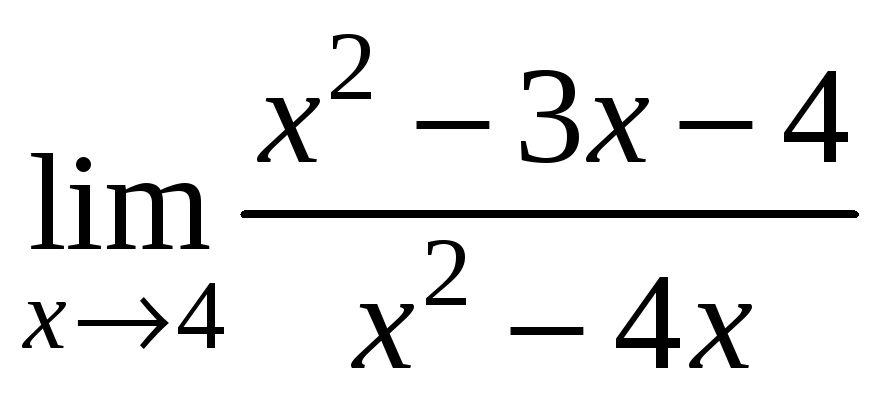 ;
3)
;
3) ;
4)
;
4)
 ;
;
5) ;
6)
;
6)
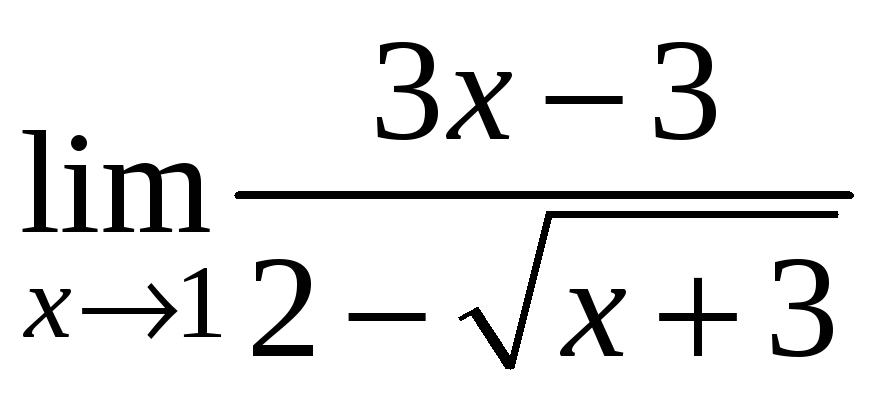 ;
7)
;
7)
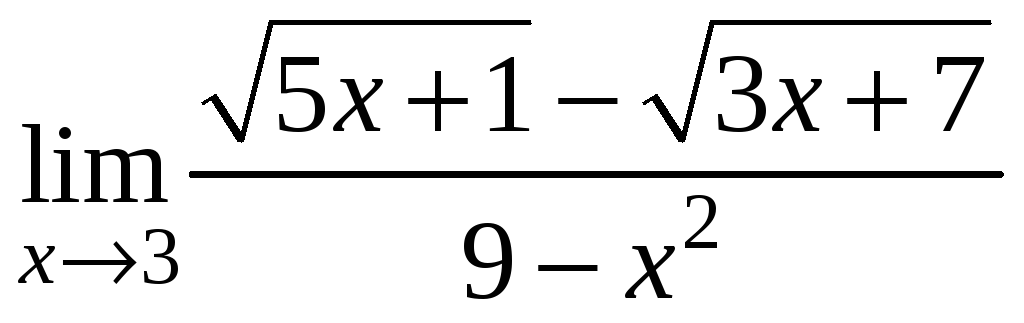 ;
;
8)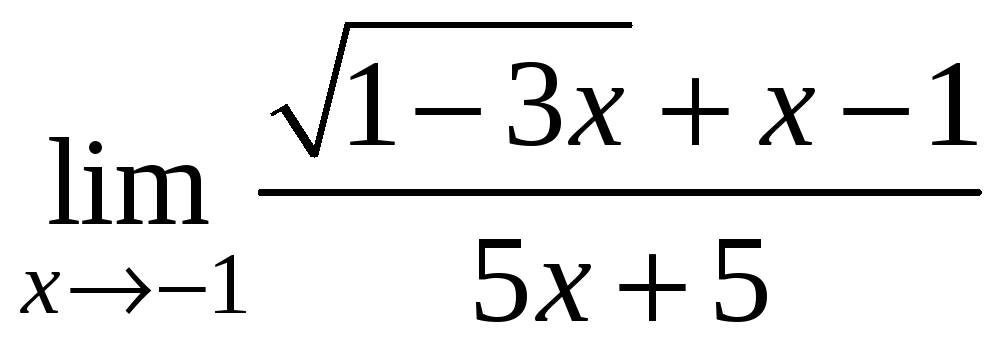 ;
9)
;
9)
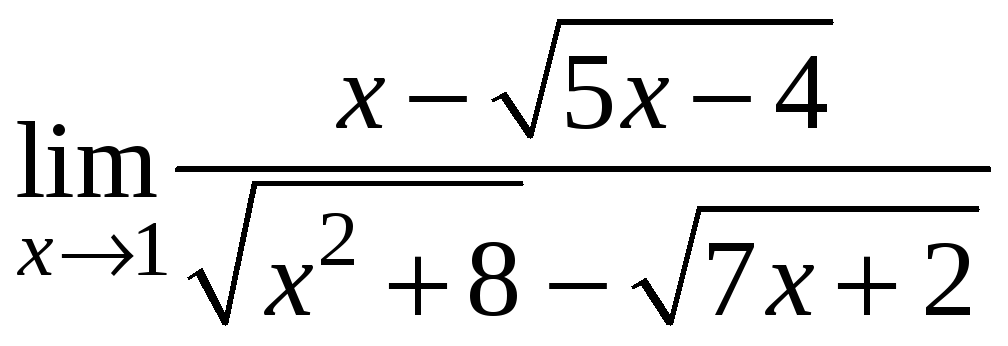 ;
10)
;
10)
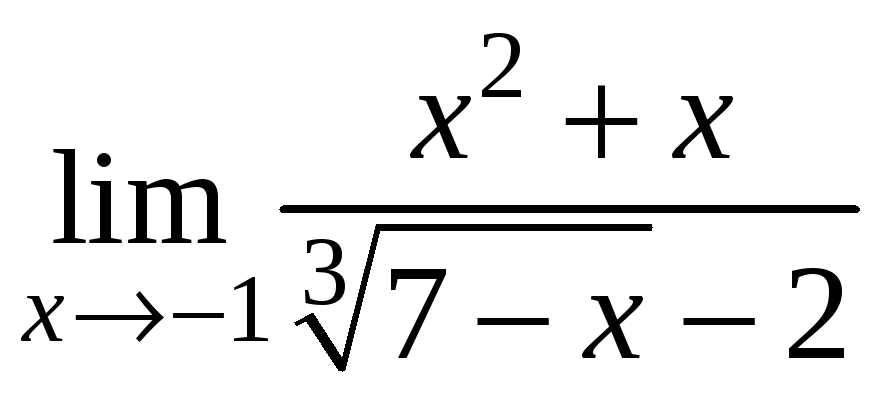 .
.
Завдання 2.9 Обчислити границі
1)
![]() ;
2)
;
2)
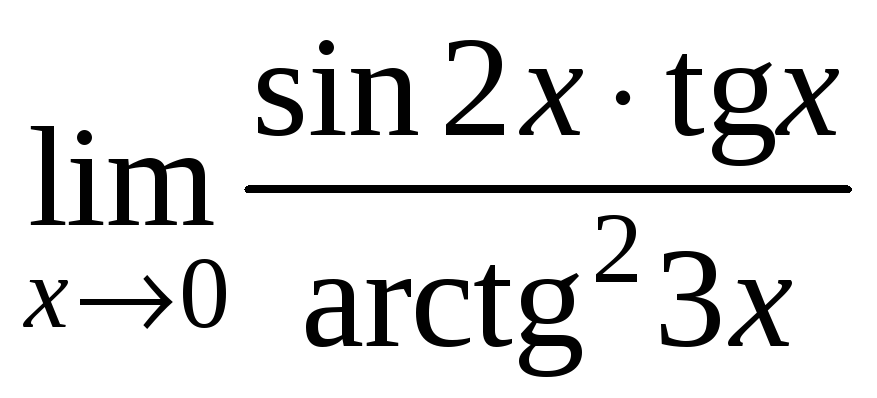 ;
3)
;
3)![]() ;
4)
;
4)
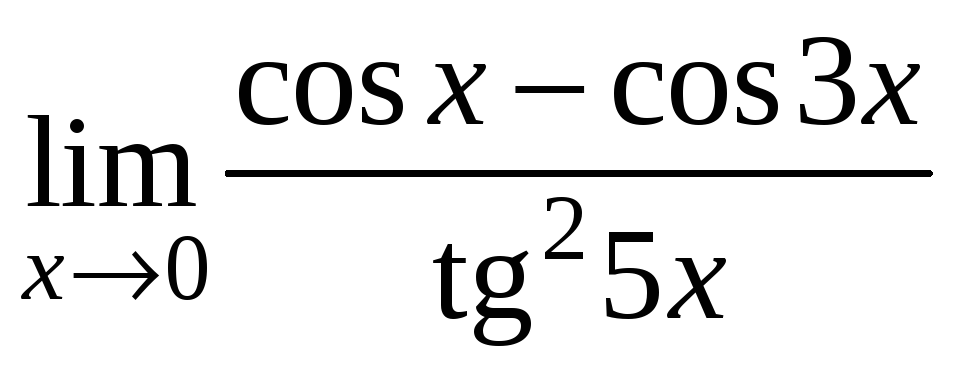 ;
;
5)
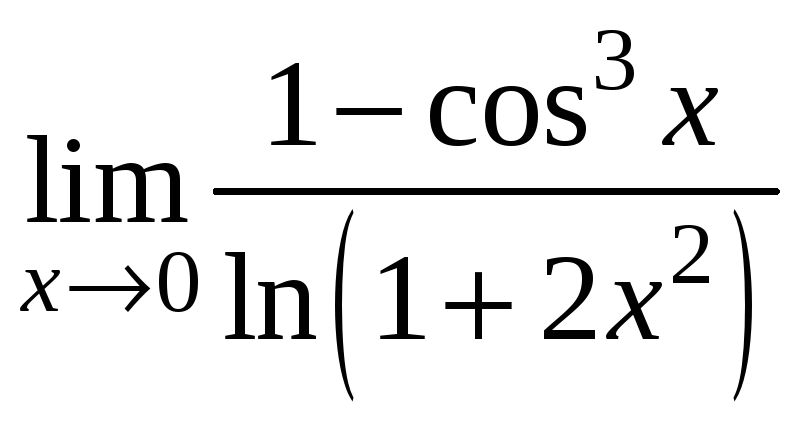 ;
6)
;
6)
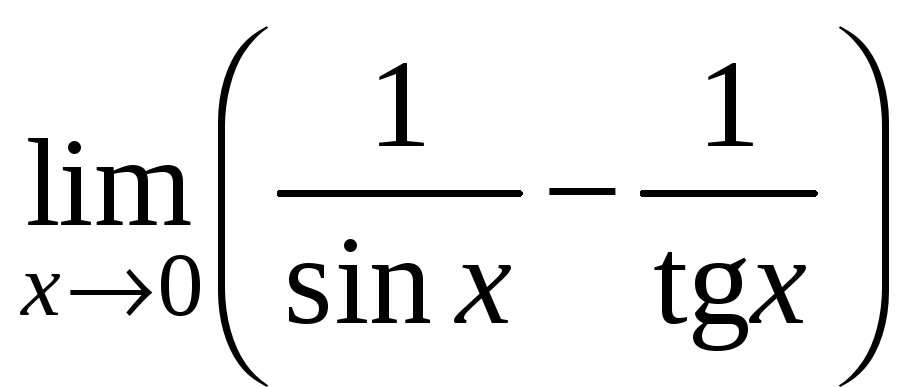 ;
7)
;
7)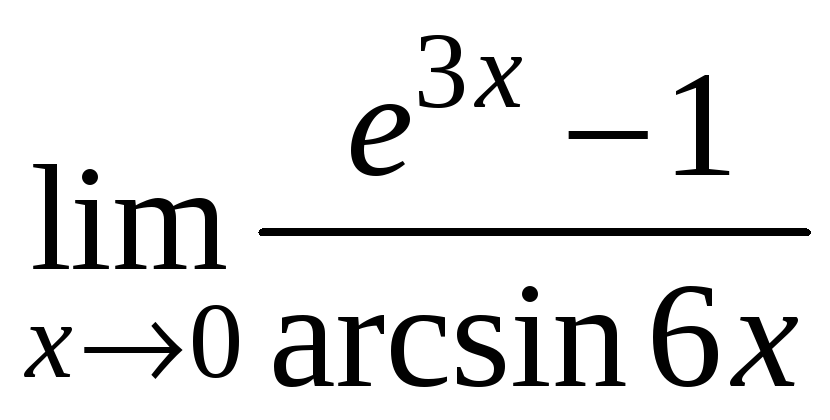 ;
8)
;
8)
![]() ;
;
9)![]() ;
10)
;
10)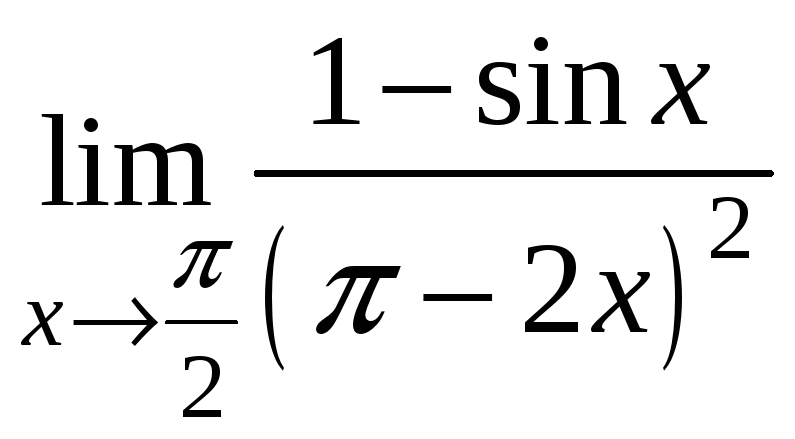 ;
11)
;
11)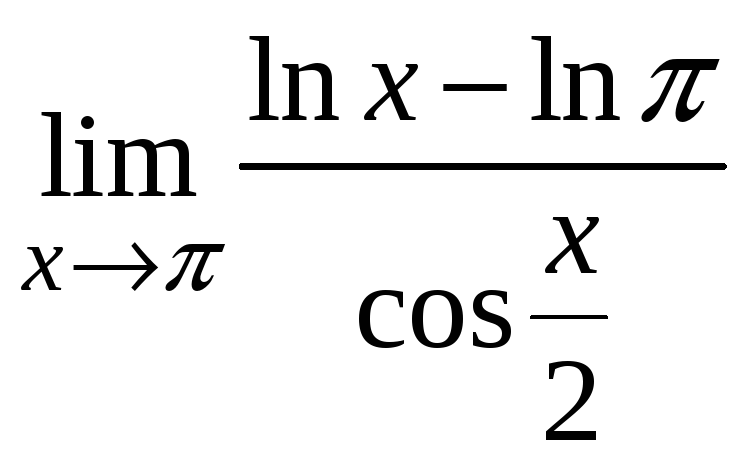 ;
12)
;
12)
![]() .
.
Завдання 2.10 Обчислити границі
1)
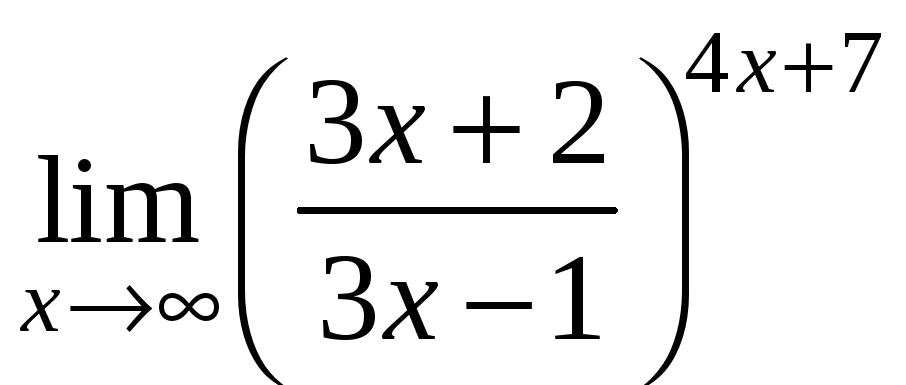 ;
2)
;
2)
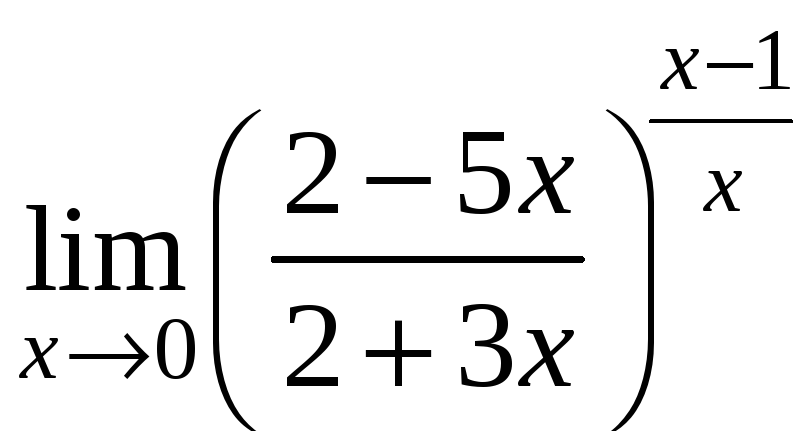 ;
3)
;
3)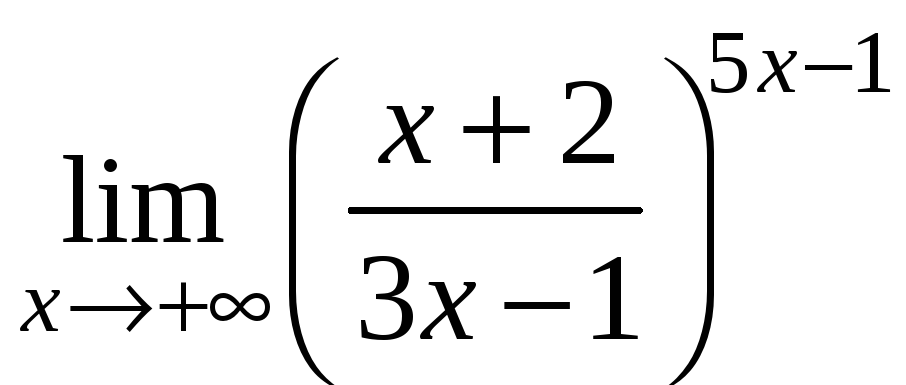 ;
;
4)
![]() ;
5)
;
5)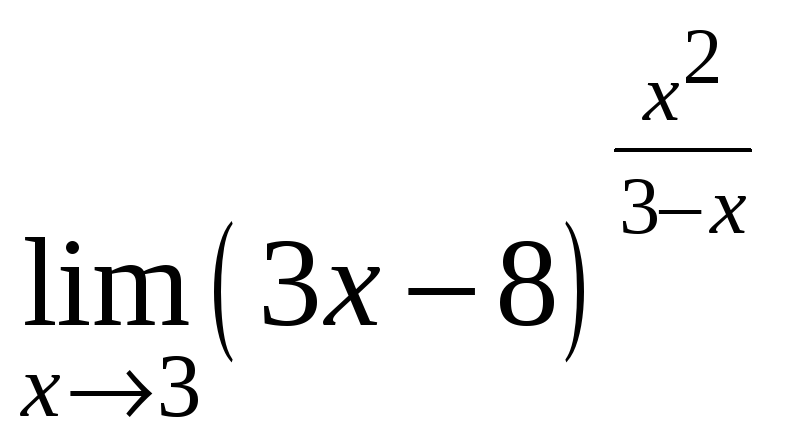 .
.
