
- •Г.В. Соколовська с.Ю. Соколовський Вступ до аналізу. Диференціальне числення функцій однієї та кількох змінних.
- •Тема 1. Границя числової послідовності
- •Тема 2. Границя та неперервність функції в точці
- •Тема 3. Точки розриву функції
- •Тема 3. Похідна та деякі її застосування
- •Тема 5. Дослідження функції
- •Тема 6. Частинні похідні функції кількох змінних та деякі їх застосування
- •Тема 7. Екстремум функції двох змінних.
Тема 5. Дослідження функції
Завдання
5.1
Для функції
![]() знайти найбільше та найменше значення
на відрізку
знайти найбільше та найменше значення
на відрізку
![]() .
.
Розв’язання
Неперервна
на заданому відрізку функція досягає
на ньому найбільшого
![]() і найменшого
і найменшого
![]() значень. Якщо найбільшого або найменшого
значення функція досягає у внутрішній
точці відрізка, то це має бути точка
екстремуму. Хоча значення
значень. Якщо найбільшого або найменшого
значення функція досягає у внутрішній
точці відрізка, то це має бути точка
екстремуму. Хоча значення
![]() або
або
![]() функція може набувати у граничній точці
відрізка.
функція може набувати у граничній точці
відрізка.
Знайдемо
критичні точки функції, які належать
відрізку
![]() .
.
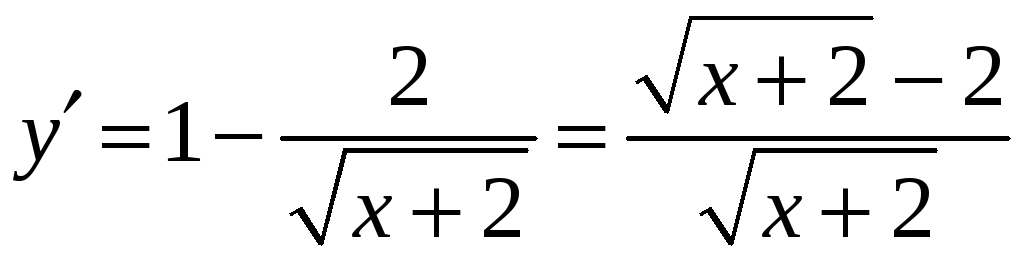 ;
;
![]() ,
якщо
,
якщо
![]() або
або
![]() ;
;
![]() не існує при
не існує при
![]() або
або
![]() .
Оскільки лише одна з критичних точок
.
Оскільки лише одна з критичних точок
![]() належить відрізку
належить відрізку
![]() ,
то знайдемо значення функції в цій точці
а також на кінцях відрізка:
,
то знайдемо значення функції в цій точці
а також на кінцях відрізка:
![]() ,
,
![]() ,
,
![]() .
.
Отже
найбільшим на відрізку
![]() значенням функції є
значенням функції є
![]() ,
а найменшим -
,
а найменшим -
![]() .
.
Завдання
5.2
Провести повне дослідження функцій і
побудувати їх графіки а)
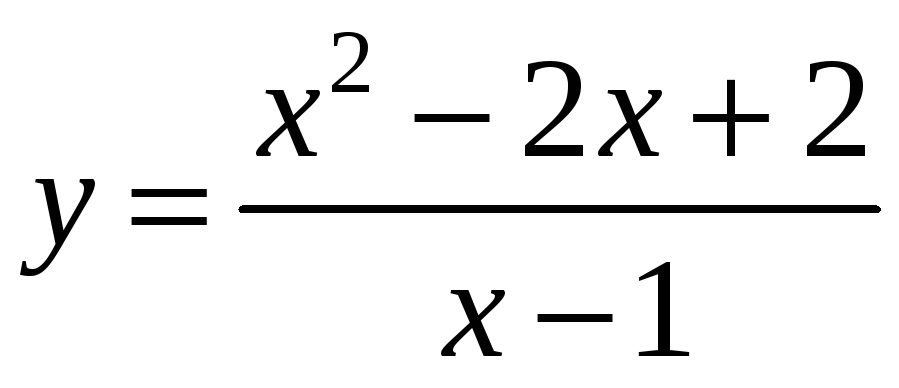 ;
б)
;
б)
![]() .
.
Розв’язання
а) 1)
Область визначення
![]() ,
тобто
,
тобто
![]() .
.
2) Графік
функції перетинає вісь
![]() в тій точці, де
в тій точці, де
![]() ,
тому
,
тому
![]() .
Точок перетину з віссю
.
Точок перетину з віссю
![]() немає, оскільки рівняння
немає, оскільки рівняння
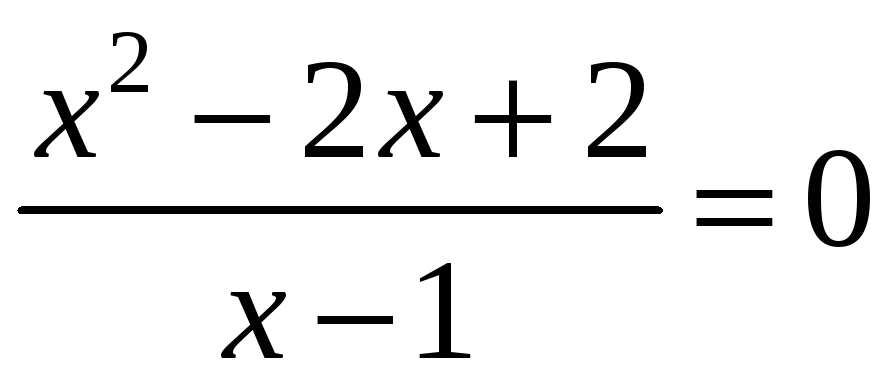 не має розв’язків.
не має розв’язків.
3) Знайдемо
інтервали, де функція зберігає постійний
знак:
![]() ,
коли
,
коли
![]() ,
,
![]() ,
якщо
,
якщо
![]() .
.
4) Парність і непарність. Періодичність.
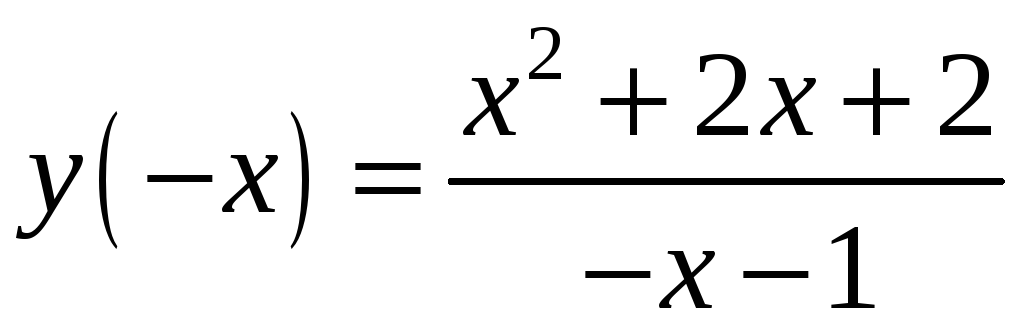 .
Функція не є парною та не є непарною,
адже
.
Функція не є парною та не є непарною,
адже
![]() та
та
![]() .
Функція неперіодична.
.
Функція неперіодична.
5) Асимптоти.
А.
![]() - точка розриву другого роду тому, що
- точка розриву другого роду тому, що
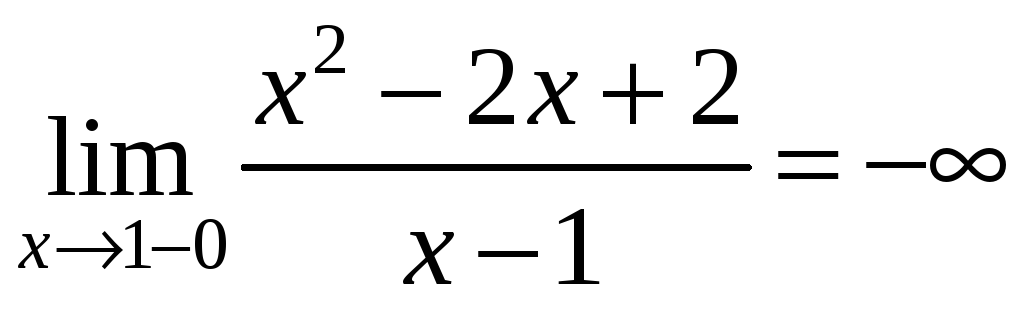 ;
;
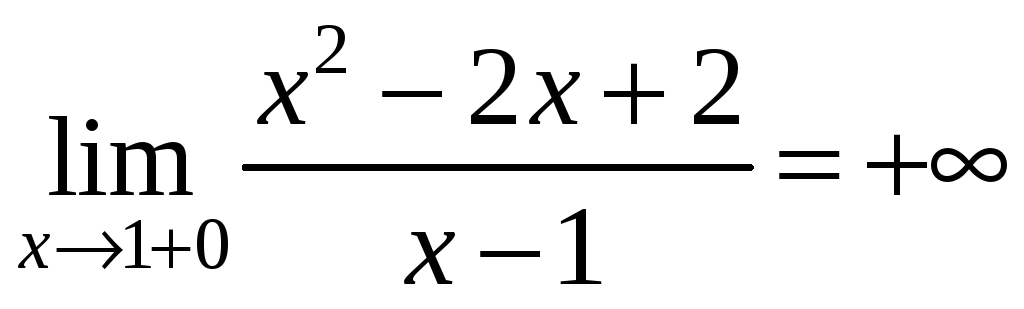 .
З цього також випливає, що пряма
.
З цього також випливає, що пряма
![]() є вертикальною асимптотою графіка.
є вертикальною асимптотою графіка.
Б.
Знайдемо невертикальну асимптоту у
вигляді
![]() ,
де
,
де
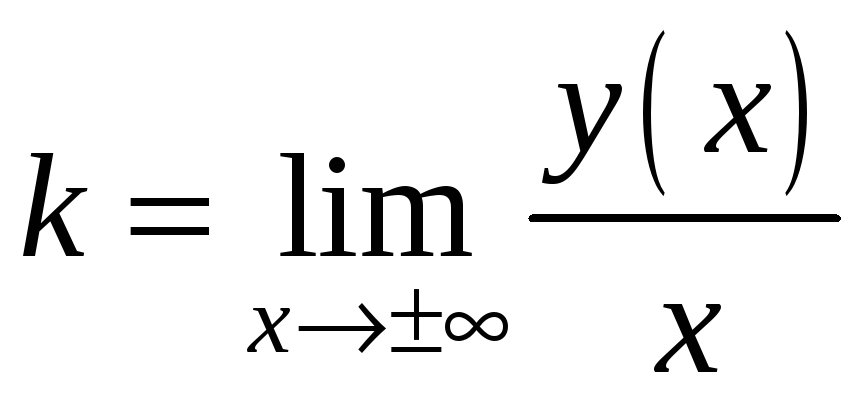 ;
;
![]() .
.
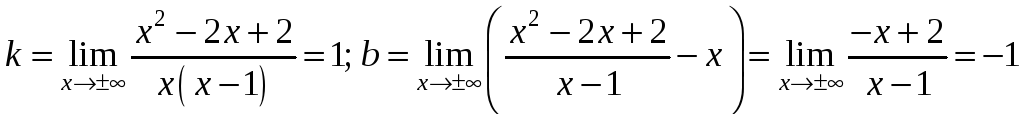 .
Отже пряма
.
Отже пряма
![]() - ліва і права невертикальна асимптота
графіка.
- ліва і права невертикальна асимптота
графіка.
6) Інтервали монотонності. Точки екстремуму.
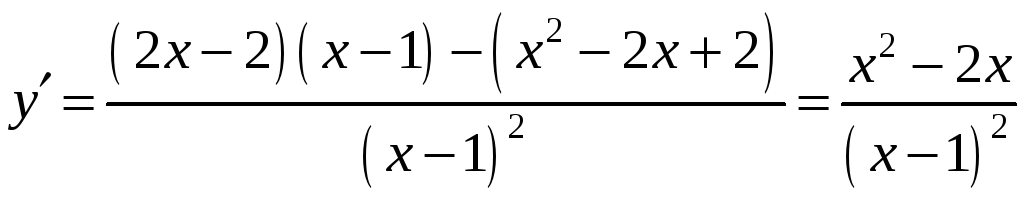 .
З умови
.
З умови
![]() (
(![]() )
знаходимо критичні точки:
)
знаходимо критичні точки:
![]() .
Вони розбивають область визначення на
інтервали:
.
Вони розбивають область визначення на
інтервали:
![]() ,
,
![]() .
При цьому
.
При цьому
![]() на інтервалах
на інтервалах
![]() та
та
![]() (функція
зростає),
(функція
зростає),
![]() на інтервалах
на інтервалах
![]() та
та
![]() (функція спадає). Тоді
(функція спадає). Тоді
![]() - точка максимуму і
- точка максимуму і
![]() ;
;
![]() - точка мінімуму і
- точка мінімуму і
![]() .
.
7) Інтервали опуклості та ввігнутості. Точки перегину.
 .
Оскільки
.
Оскільки
![]() відмінна
від нуля у будь-якій точці, то критичною
точкою другого порядку є лише
відмінна
від нуля у будь-якій точці, то критичною
точкою другого порядку є лише
![]() .
При цьому
.
При цьому
![]() на інтервалі
на інтервалі
![]() ,
отже на цьому інтервалі графік опуклий;
,
отже на цьому інтервалі графік опуклий;
![]() на інтервалі
на інтервалі
![]() - графік ввігнутий. Точок перегину
немає, оскільки в точці
- графік ввігнутий. Точок перегину
немає, оскільки в точці
![]() функція невизначена. За результатами
дослідження побудуємо графік функції
(рис. 3).
функція невизначена. За результатами
дослідження побудуємо графік функції
(рис. 3).
б) 1)
Область визначення
![]() .
.
2) Графік
функції перетинає вісь
![]() в точці
в точці
![]() ,
,![]() .
В цій же точці графік перетинає вісь
.
В цій же точці графік перетинає вісь
![]() .
.
3)
![]() на інтервалі
на інтервалі
![]() ,
а
,
а
![]() при
при
![]() .
.
4) Парність і непарність. Періодичність.
![]() .
Функція не є ні парною ні непарною, адже
.
Функція не є ні парною ні непарною, адже
![]() та
та
![]() .
Функція неперіодична.
.
Функція неперіодична.
5) Асимптоти.
А. Точок розриву немає, отже немає вертикальних асимптот.
Б.
Знайдемо праву невертикальну асимптоту
у вигляді
![]() ,
де
,
де
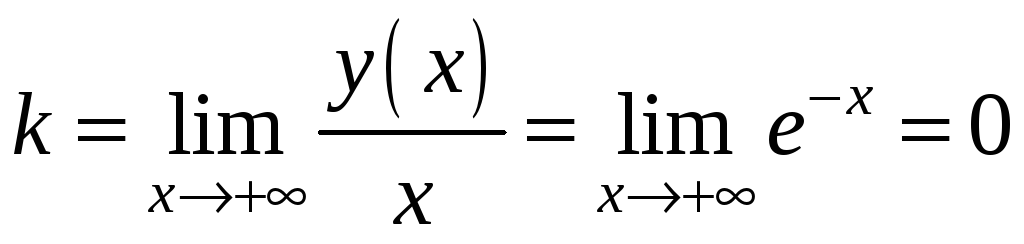 ;
;
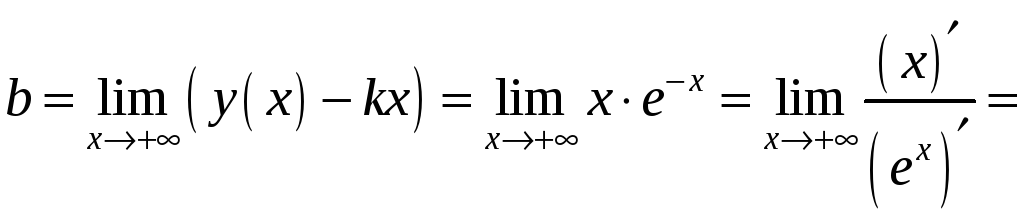
![]() .
Таким чином пряма
.
Таким чином пряма
![]() - права горизонтальна асимптота. Оскільки
при
- права горизонтальна асимптота. Оскільки
при
![]() маємо:
маємо:
 ,
то лівої невертикальної асимптоти у
графіка немає.
,
то лівої невертикальної асимптоти у
графіка немає.
6) Інтервали монотонності. Точки екстремуму.
![]() .
З умови
.
З умови
![]() одержимо критичну точку
одержимо критичну точку
![]() .
При цьому
.
При цьому
![]() при
при
![]() (функція зростає),
(функція зростає),
![]() при
при
![]() (функція спадає). Тоді
(функція спадає). Тоді
![]() - точка максимуму і
- точка максимуму і
![]() .
.
7) Інтервали опуклості та ввігнутості. Точки перегину.
![]() .
Прирівняємо її до нуля:
.
Прирівняємо її до нуля:
![]() ,
тоді
,
тоді
![]() .
При цьому
.
При цьому
![]() на інтервалі
на інтервалі
![]() (графік опуклий);
(графік опуклий);
![]() на інтервалі
на інтервалі
![]() (графік увігнутий). Отже
(графік увігнутий). Отже
![]() - абсциса точки перегину і
- абсциса точки перегину і
![]() .
За результатами дослідження побудуємо
графік функції (рис. 4).
.
За результатами дослідження побудуємо
графік функції (рис. 4).

Завдання
5.3
Під час підготовки до іспиту студент
за
![]() днів вивчає таку частину всього курсу:
днів вивчає таку частину всього курсу:
![]() ,
а забуває таку:
,
а забуває таку:
![]() .
Скільки днів треба витратити на
підготовку, щоб засвоєна частина була
найбільшою?
.
Скільки днів треба витратити на
підготовку, щоб засвоєна частина була
найбільшою?
Розв’язання
Складемо
функцію, що виражає залежність засвоєної
частини курсу від кількості днів
![]() ,
витрачених на підготовку:
,
витрачених на підготовку:
![]() .
Знайдемо її найбільше значення на
проміжку
.
Знайдемо її найбільше значення на
проміжку
![]() ,
якщо вона цього значення досягає.
Знайдемо похідну
,
якщо вона цього значення досягає.
Знайдемо похідну
![]() .
Маємо:
.
Маємо:
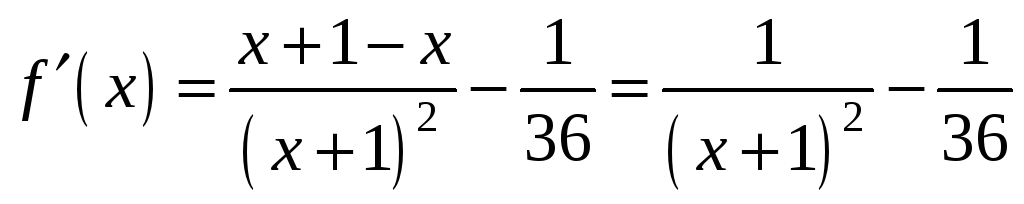 .
Знайдемо критичні точки, що належать
проміжку
.
Знайдемо критичні точки, що належать
проміжку
![]() .
Маємо:
.
Маємо:
![]() ,
якщо
,
якщо
![]() ,
тобто
,
тобто
![]() .
Зауважимо, що
.
Зауважимо, що
![]() ,
коли
,
коли
![]() ( функція зростає),
( функція зростає),
![]() ,
коли
,
коли
![]() ( функція спадає). Отже на проміжку
( функція спадає). Отже на проміжку
![]() неперервна функція
неперервна функція
![]() має лише одну точку екстремуму, це точка
максимуму
має лише одну точку екстремуму, це точка
максимуму
![]() .
Тоді в цій точці функція досягає свого
найбільшого на цьому проміжку значення
.
Тоді в цій точці функція досягає свого
найбільшого на цьому проміжку значення
![]() .
Таким чином, студентові треба витратити
на підготовку 5 днів, щоб засвоєна частина
курсу була найбільшою.
.
Таким чином, студентові треба витратити
на підготовку 5 днів, щоб засвоєна частина
курсу була найбільшою.
Завдання для самостійного розв’язування
Завдання 5.4 Провести повне дослідження функцій і побудувати їх графіки.
1)
![]() ;
2)
;
2)
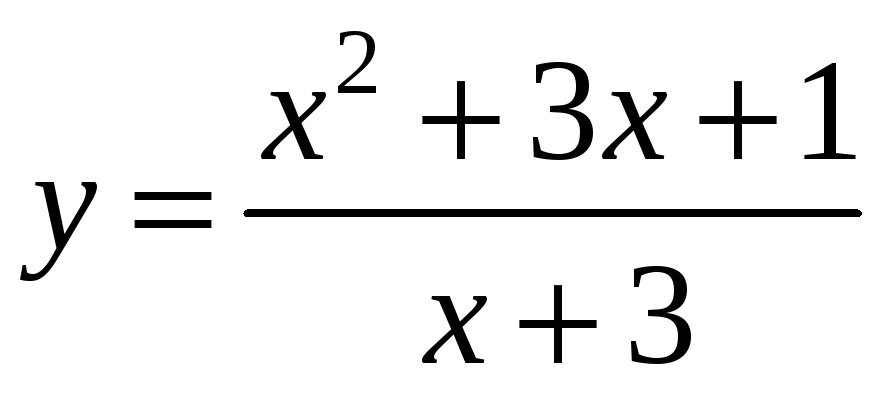 ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
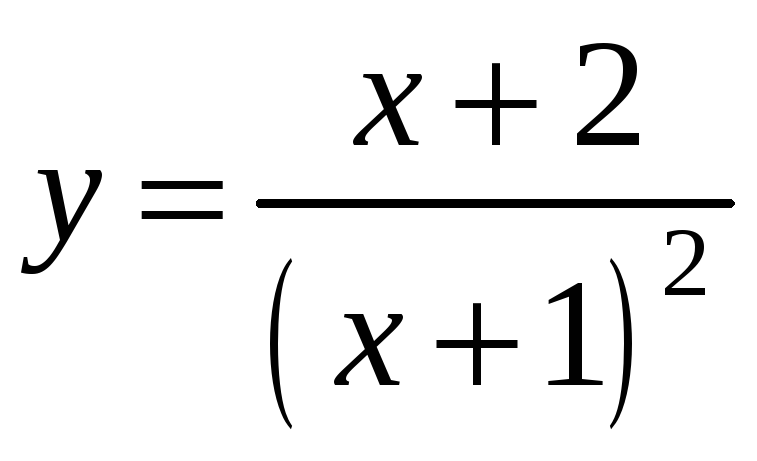 ;
8)
;
8)
![]() ;
9)
;
9)
![]() ;
;
10)
![]() ;
11)
;
11)
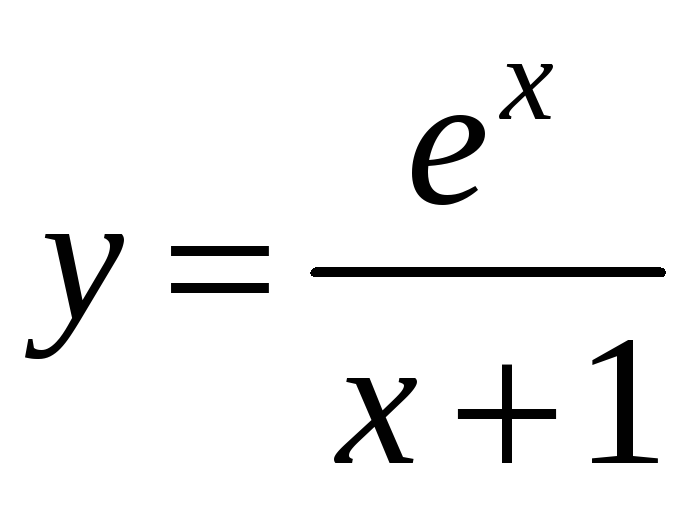 ;
12)
;
12)
 ;
13)
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
![]() .
.
Завдання 5.5 Знайти найбільше і найменше значення функції на заданому відрізку.
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
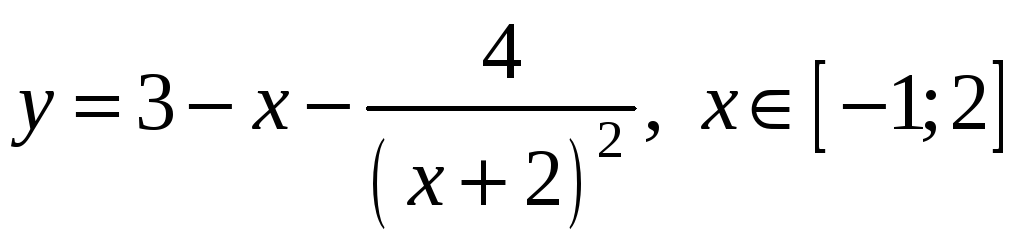 ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() .
.
Завдання 5.6 Сума двох додатних чисел дорівнює 10. Знайти можливий найбільший добуток цих чисел.
Завдання 5.7 Число 54 представити у вигляді суми трьох доданків, перший з яких удвічі більший від другого. Знайти ці доданки так, щоб їх добуток був найбільшим.
Завдання
5.8
З дроту довжини
![]() треба виготовити прямокутну рамку
найбільшої площі. Знайти розміри рамки.
треба виготовити прямокутну рамку
найбільшої площі. Знайти розміри рамки.
Завдання
5.9
Знайти найбільший об’єм циліндра, площа
поверхні якого дорівнює
![]() .
.
Завдання
5.10
Вікно має форму прямокутника, завершеного
півколом (рис. 5). Периметр вікна дорівнює
![]() .
При якому радіусі півкола воно буде
пропускати максимальну кількість
світла?
.
При якому радіусі півкола воно буде
пропускати максимальну кількість
світла?

Завдання
5.11
Тіло масою
![]() падає з висоти
падає з висоти
![]() і втрачає масу (згорає) пропорційно до
часу падіння, коефіцієнт пропорційності
і втрачає масу (згорає) пропорційно до
часу падіння, коефіцієнт пропорційності
![]() .
Вважаючи, що початкова швидкість
.
Вважаючи, що початкова швидкість
![]() ,
а прискорення
,
а прискорення
![]() ,
знайти найбільшу кінетичну енергію
тіла (
,
знайти найбільшу кінетичну енергію
тіла (![]() ).
Силою опору повітря знехтувати.
).
Силою опору повітря знехтувати.
Завдання
5.12
На параболі
![]() знайти точку найменш віддалену від
прямої
знайти точку найменш віддалену від
прямої
![]() .
Знайти цю відстань.
.
Знайти цю відстань.
