
- •Г.В. Соколовська с.Ю. Соколовський Вступ до аналізу. Диференціальне числення функцій однієї та кількох змінних.
- •Тема 1. Границя числової послідовності
- •Тема 2. Границя та неперервність функції в точці
- •Тема 3. Точки розриву функції
- •Тема 3. Похідна та деякі її застосування
- •Тема 5. Дослідження функції
- •Тема 6. Частинні похідні функції кількох змінних та деякі їх застосування
- •Тема 7. Екстремум функції двох змінних.
Тема 3. Точки розриву функції
Завдання 3.1 Знайти точки розриву функції
 та
вказати їх тип.
та
вказати їх тип.
Розв’язання
Зауважимо,
що точка
![]() називається точкою розриву функції
називається точкою розриву функції
![]() ,
якщо в цій точці функція не є неперервною,
тобто порушається рівність
,
якщо в цій точці функція не є неперервною,
тобто порушається рівність
![]() .
Виконання ж цієї рівності означає, що
.
Виконання ж цієї рівності означає, що
1) існують
скінченні односторонні границі
![]() та
та
![]() ;
;
2)
![]() ;
;
3) обидві
односторонні границі функції
![]() в точці
в точці
![]() дорівнюють
дорівнюють
![]() .
.
Отже в
точці розриву хоча б одна з цих умов
порушується. Якщо в точці розриву
виконано тільки умову 1, то
![]() називають точкою розриву першого роду.
Якщо порушається умова 1 (тобто хоча б
одна з односторонніх границь не існує
або дорівнює
називають точкою розриву першого роду.
Якщо порушається умова 1 (тобто хоча б
одна з односторонніх границь не існує
або дорівнює
![]() ),
то
),
то
![]() називають точкою розриву другого роду.
Якщо порушається лише умова 3, то
називають точкою розриву другого роду.
Якщо порушається лише умова 3, то
![]() називають точкою усувного розриву.
називають точкою усувного розриву.
Оскільки
кожна з чотирьох функцій, що задають
![]() в
цьому завданні на відповідних інтервалах
є неперервною, то слід підозрювати
наявність розриву лише в точках
в
цьому завданні на відповідних інтервалах
є неперервною, то слід підозрювати
наявність розриву лише в точках
![]() .
Дослідимо кожну з них.
.
Дослідимо кожну з них.
Оскільки
![]() ,
,![]() ,
,
![]() ,
то
,
то
![]() – точка розриву другого роду.
– точка розриву другого роду.
![]() ,
,
![]() ,
,
![]() .
Отже в точці
.
Отже в точці
![]() – функція неперервна.
– функція неперервна.
В точці
![]() маємо:
маємо:
![]() ,
,
![]() ,
,
![]()
![]() .
Тоді
.
Тоді
![]() – точка розриву першого роду.
– точка розриву першого роду.
Зобразимо графік цієї функції (рис.1).
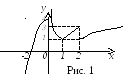
Завдання
3.2
Знайти точки розриву функції
![]() та вказати їх тип.
та вказати їх тип.
Розв’язання
Задана
функція є елементарною, тому вона
неперервна в своїй області визначення:
![]() або
або
![]() .
В точках
.
В точках
![]() та
та
![]() вона має розриви, оскільки в цих точках
функція невизначена. Знайдемо границі:
вона має розриви, оскільки в цих точках
функція невизначена. Знайдемо границі:
 ,
,
![]() .
.
![]() .
Це означає, що
.
Це означає, що
![]() - точка розриву другого роду, а
- точка розриву другого роду, а
![]() - точка усувного розриву. Зобразимо
графік функції, враховуючи те, що всюди,
окрім точки
- точка усувного розриву. Зобразимо
графік функції, враховуючи те, що всюди,
окрім точки
![]() він співпадає з графіком функції
він співпадає з графіком функції
![]() .
.
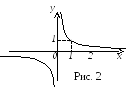
Завдання для самостійного розв’язування
Завдання
3.3
Знайти точки розриву функції
![]() та вказати їх тип.
та вказати їх тип.
1)
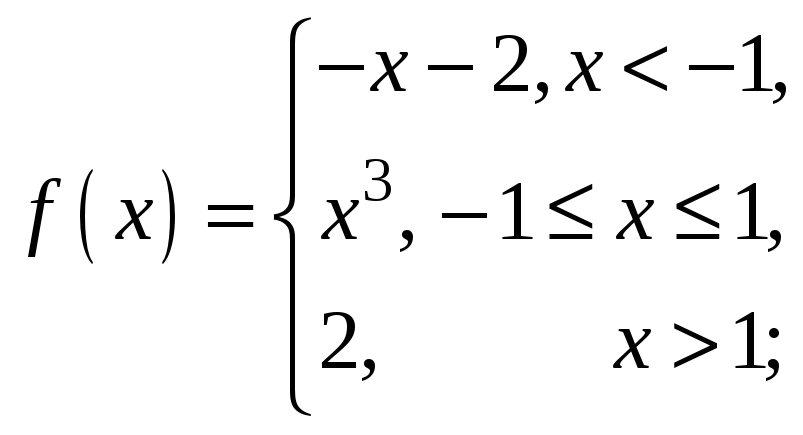 2)
2)
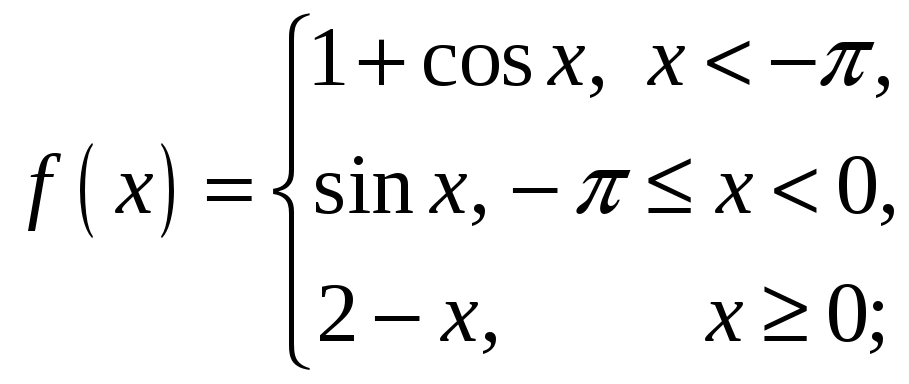 3)
3)
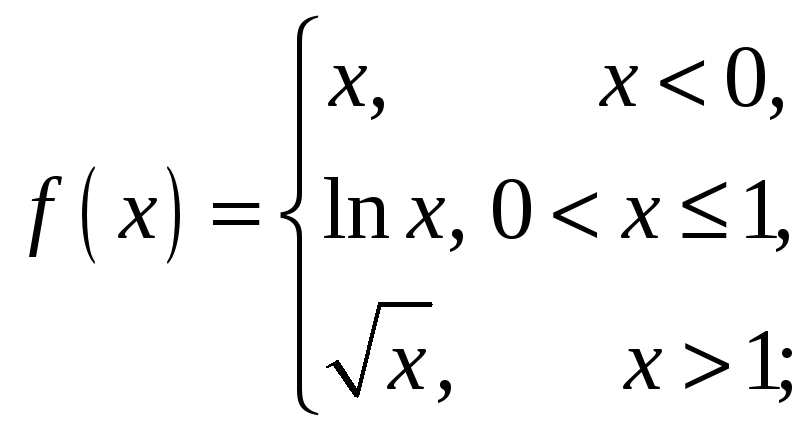
4)
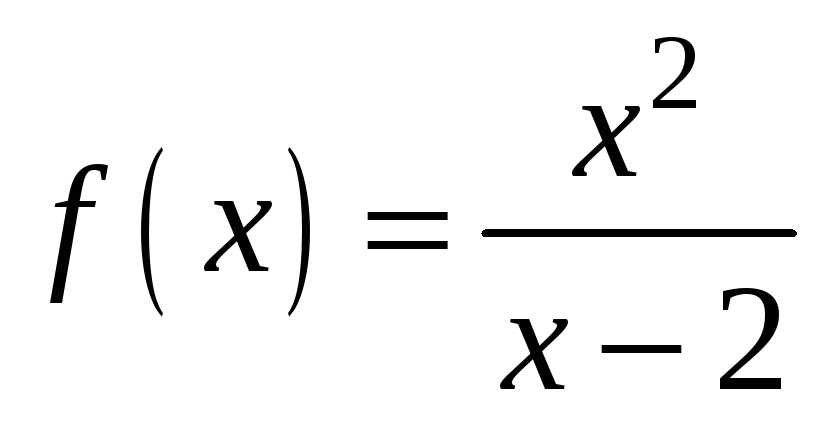 ;
5)
;
5)
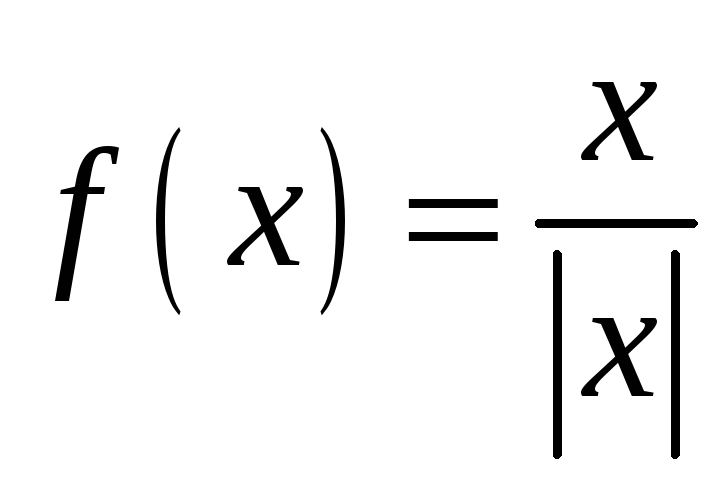 ;
6)
;
6)
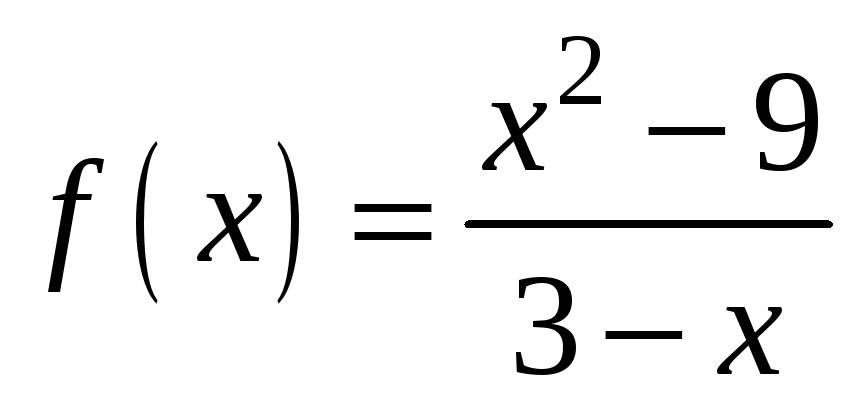 ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
9)
;
9)
 ;
10)
;
10)
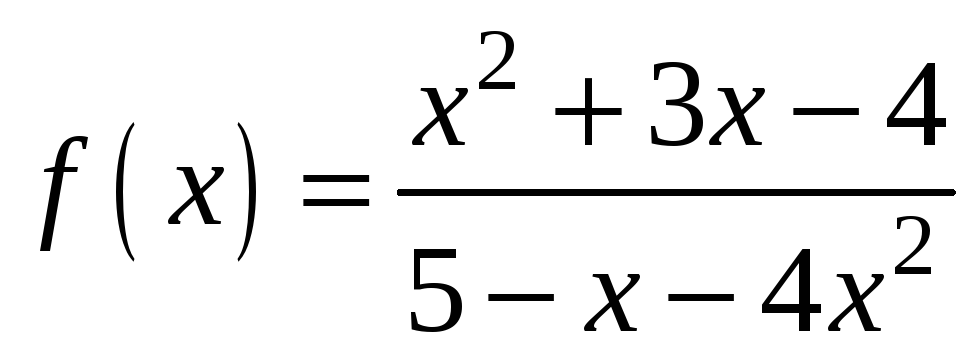 ;
11)
;
11)
![]() .
.
Тема 3. Похідна та деякі її застосування
Завдання
4.1
Знайти похідну функції
![]() в точці
в точці
![]() за означенням.
за означенням.
Розв’язання
Нагадаємо,
що похідною функції
![]() в точці
в точці
![]() називається границя відношення приросту
функції
називається границя відношення приросту
функції
![]() до приросту аргументу
до приросту аргументу
![]() за умови, що
за умови, що
![]() .
.
Надамо
аргументові приросту
![]() і знайдемо значення функції в точці
і знайдемо значення функції в точці
![]() :
:![]() .
Тоді
.
Тоді
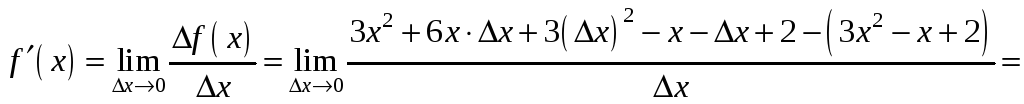
 .
.
Отже
![]() .
.
Завдання 4.2 Знайти похідну заданої функції
1)
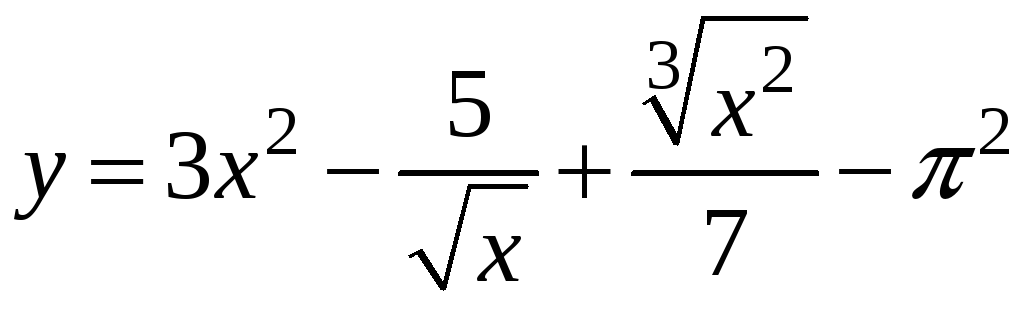 ;
2)
;
2)
 ;
3)
;
3)
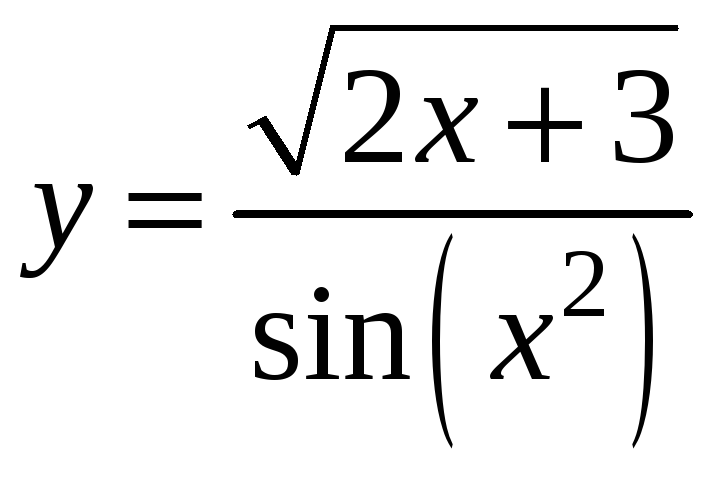 ;
;
4)
![]() ;
5)
;
5)
 ;
6)
;
6)
 .
.
Розв’язання
1)
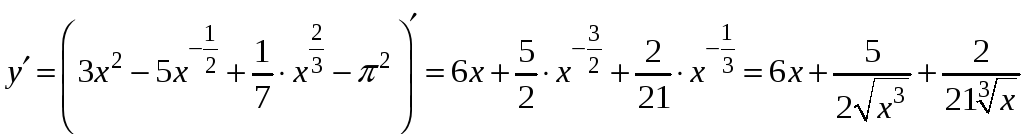 .
.
2)
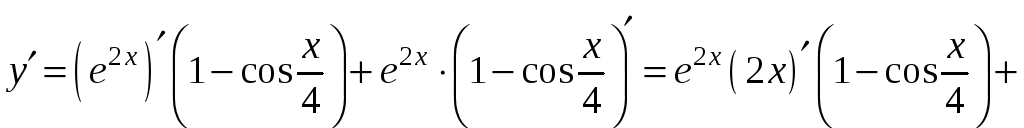
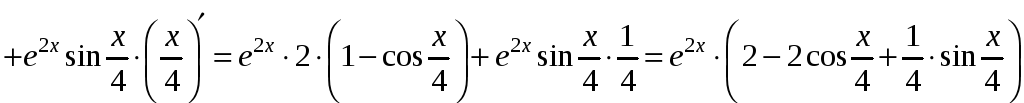 .
.
3)
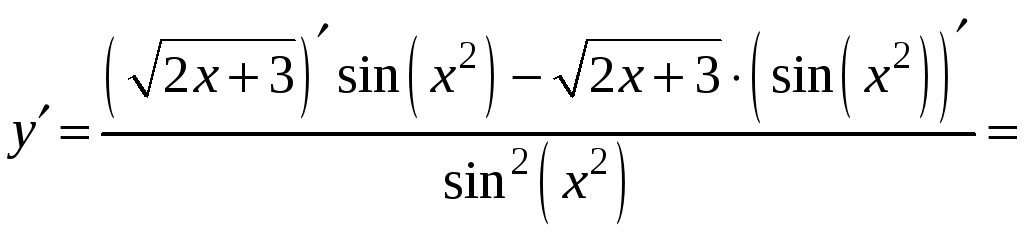
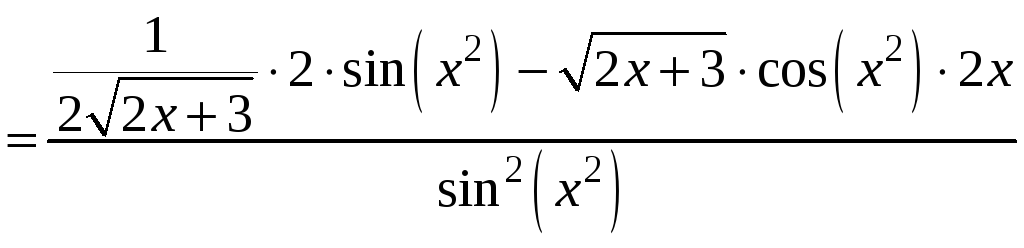
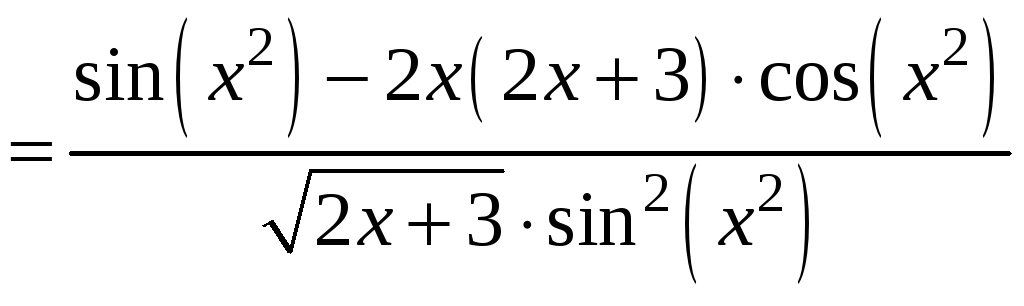 .
.
4)
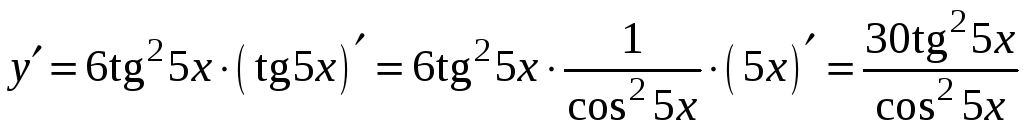 .
.
5)
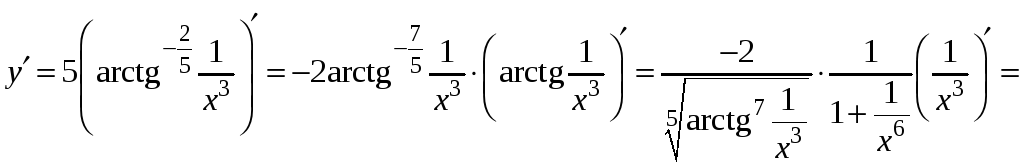
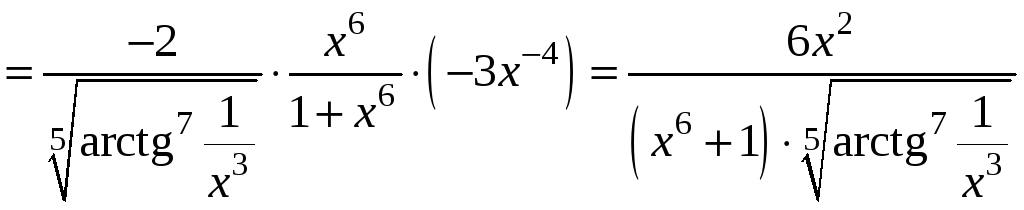 .
.
6) Для знаходження похідної параметрично заданої функції, скористаємось формулою
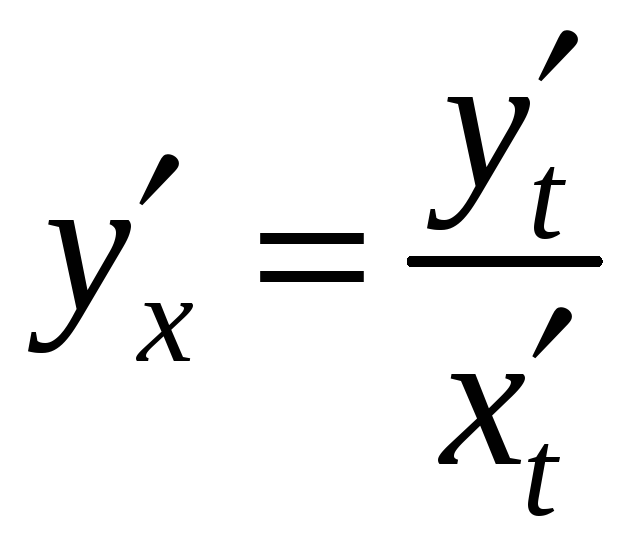 .
.
![]()
Знайдемо
![]() ,
,
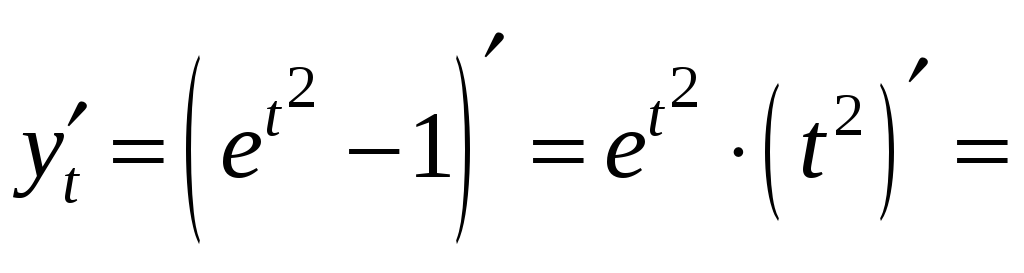
![]() .
Тоді
.
Тоді
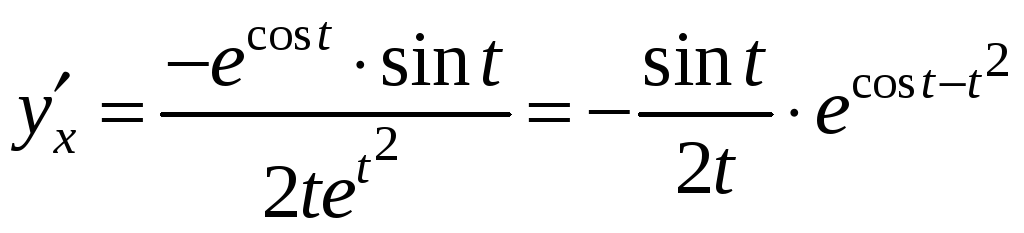 .
.
Завдання
4.3
Записати рівняння дотичної та нормалі
до графіка функції
![]() в точці з абсцисою
в точці з абсцисою
![]() .
.
Розв’язання
Рівняння
дотичної до графіка функції
![]() в точці з абсцисою
в точці з абсцисою
![]() має вигляд:
має вигляд:
![]() ,
де
,
де
![]() .
.
![]()
В цій
задачі
![]() ,
,
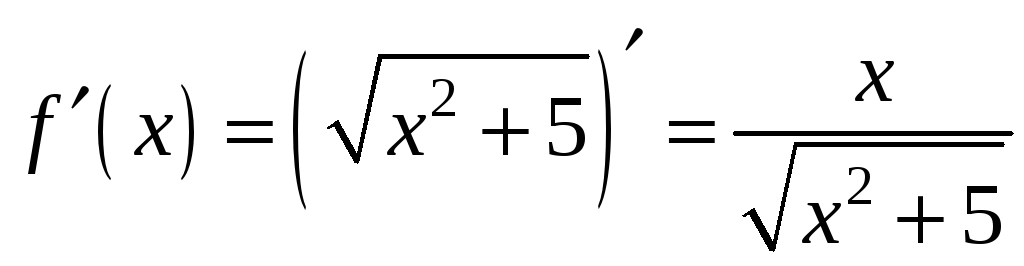 ,
,
![]() .
Тоді отримаємо рівняння дотичної:
.
Тоді отримаємо рівняння дотичної:
![]() або
або
![]() .
.
Нормаль – це пряма, що перпендикулярна до дотичної в точці дотику. Тому її рівняння має вигляд:
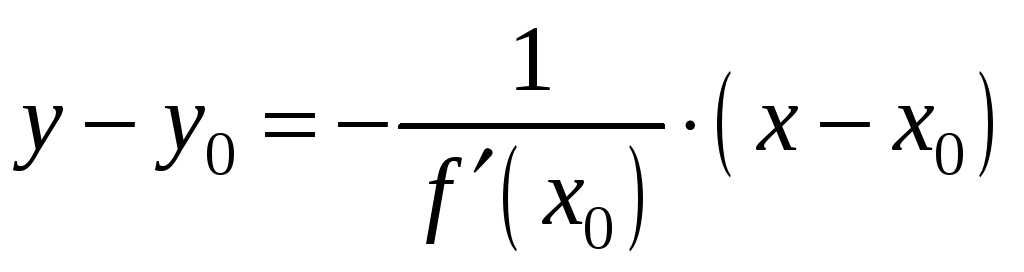 .
.
![]()
В нашому
випадку точка дотику
![]() .
Запишемо рівняння нормалі:
.
Запишемо рівняння нормалі:
![]() або
або
![]() .
.
Завдання
4.4
Записати рівняння дотичної та нормалі
до кривої
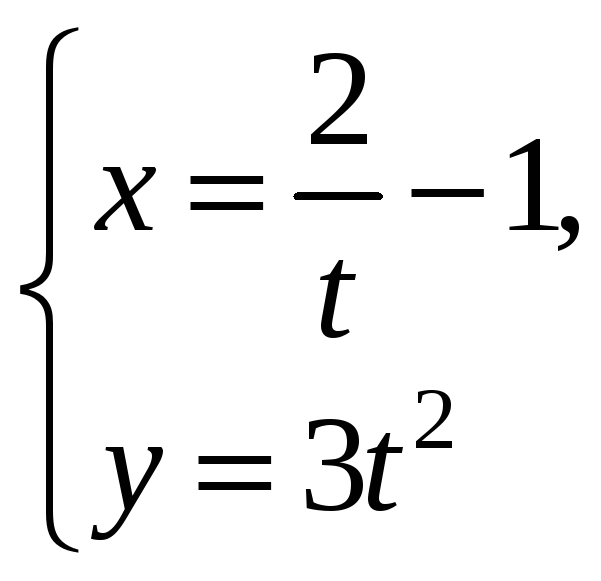 в точці, де
в точці, де
![]() .
.
Розв’язання
Знайдемо
координати точки дотику.
![]() .
Похідну обчислимо за формулою
.
Похідну обчислимо за формулою
![]() .
.
![]() .
Тоді
.
Тоді
![]() .
За формулами
.
За формулами
![]() та
та
![]() складаємо рівняння дотичної та нормалі:
складаємо рівняння дотичної та нормалі:
![]() - дотична,
- дотична,
![]() - нормаль.
- нормаль.
Завдання 4.5 Обчислити границі за допомогою правила Лопіталя
1)
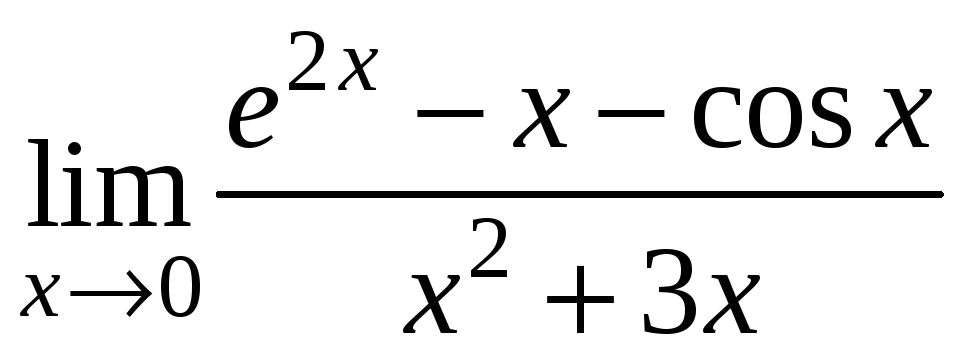 ;
2)
;
2)
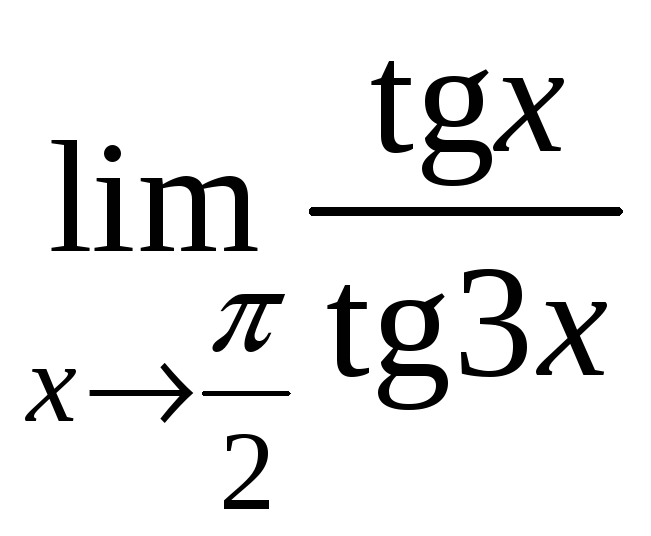 .
.
Розв’язання
1)
Сформулюємо правило Лопіталя. Нехай
![]() або
або
![]() (
(![]() -
число, або символ
-
число, або символ
![]() ).
Похідні
).
Похідні
![]() існують в деякому околі точки
існують в деякому околі точки
![]() (окрім, можливо, самої точки
(окрім, можливо, самої точки
![]() )
та існує скінченна або нескінченна
границя
)
та існує скінченна або нескінченна
границя
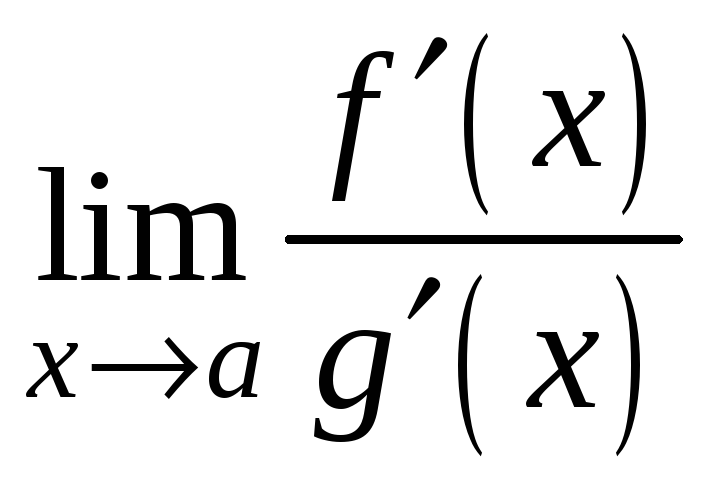 .
Тоді
.
Тоді
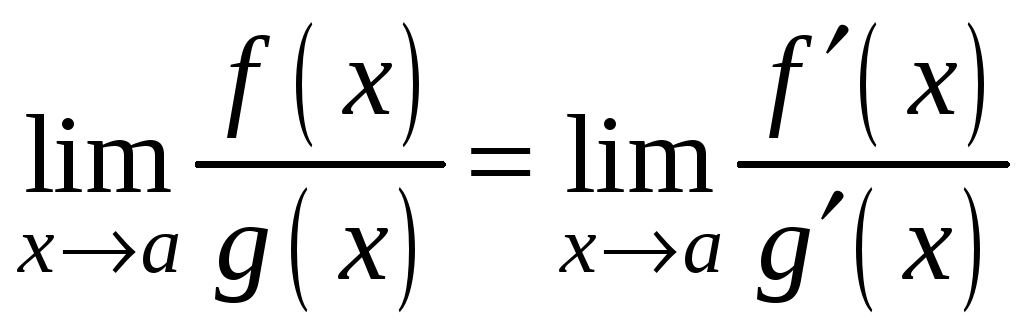 .
.
В цьому
прикладі маємо невизначеність виду
![]() .
Застосувавши правило Лопіталя, одержимо:
.
Застосувавши правило Лопіталя, одержимо:
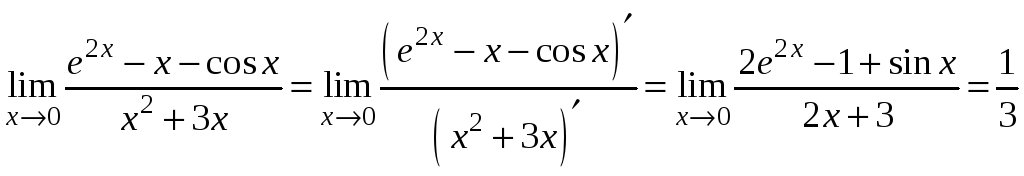 .
.
2) Тут
маємо невизначеність виду
![]() .
Застосуємо правило Лопіталя.
.
Застосуємо правило Лопіталя.
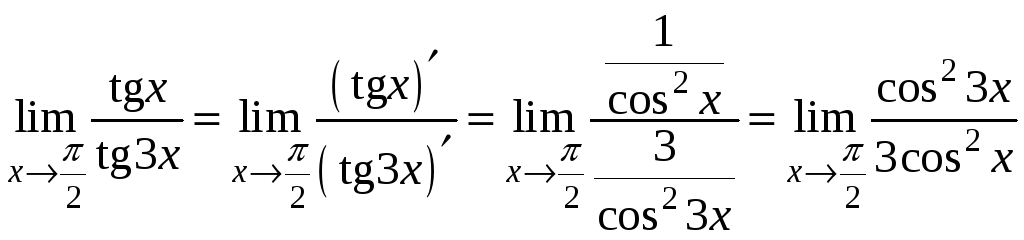 .
Тепер отримали невизначеність виду
.
Тепер отримали невизначеність виду
![]() ,
для її розкриття двічі застосуємо
правило Лопіталя.
,
для її розкриття двічі застосуємо
правило Лопіталя.
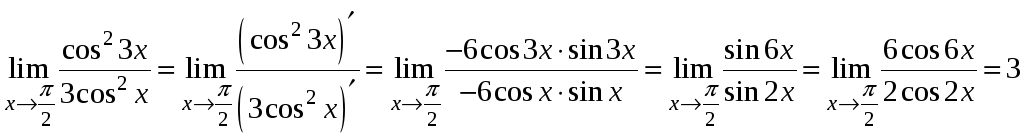
Завдання
4.6
Знайти похідні другого порядку
![]() .
.
1)
![]() ;
2)
;
2)
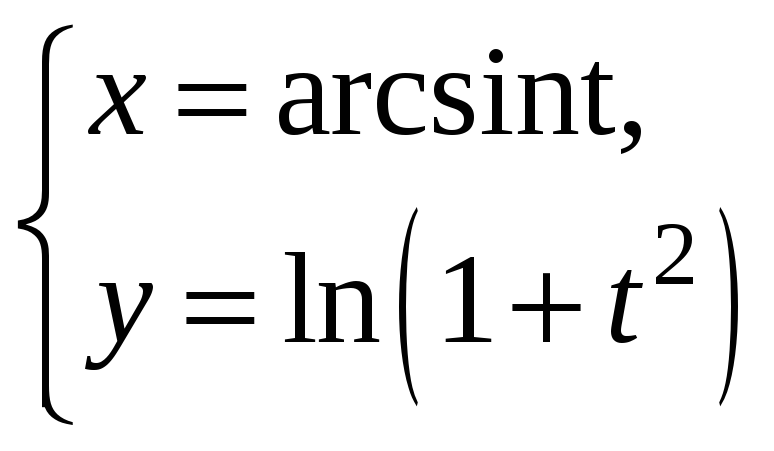 .
.
Розв’язання
1) Обчислимо спочатку похідну першого порядку.
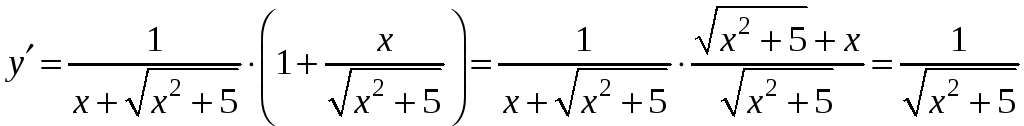 .
.
Тепер
продиференціюємо
![]() і одержимо похідну другого порядку:
і одержимо похідну другого порядку:
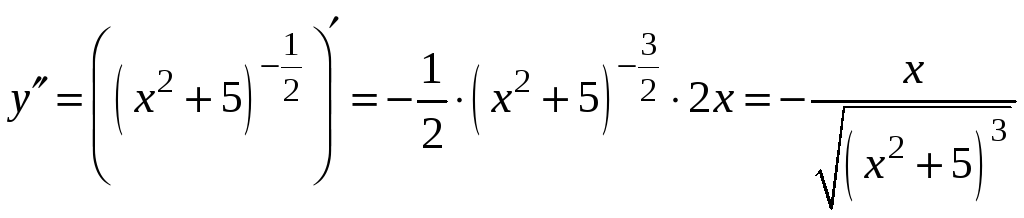 .
.
2)
Обчислимо похідну першого порядку
параметрично заданої функції за формулою
![]() .
.
 .
Отже похідна
.
Отже похідна
![]() є функцією параметрично заданою
формулами:
є функцією параметрично заданою
формулами:
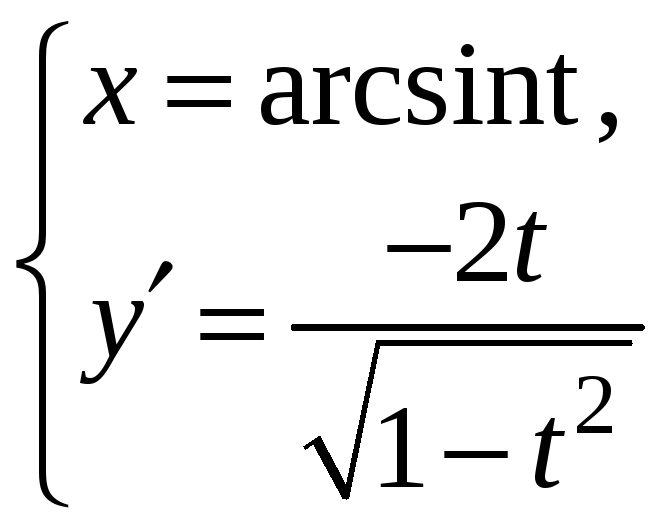 .
.
Застосувавши
до неї формулу
![]() одержимо похідну другого порядку:
одержимо похідну другого порядку:
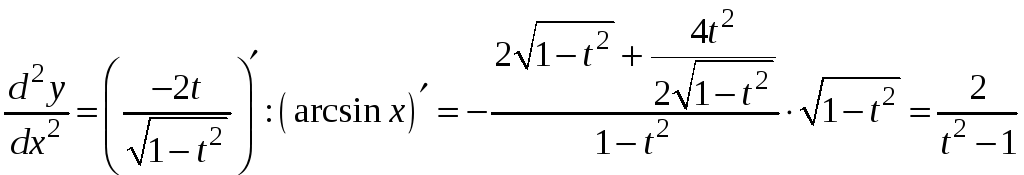 .
.
Завдання для самостійного розв’язування
Завдання
4.7
Знайти за означенням похідну функції
![]() в точці
в точці
![]() .
.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
Завдання 4.8 Знайти похідну заданої функції
1)
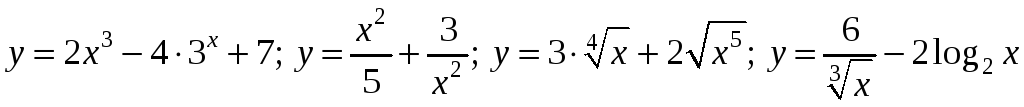 ;
;
2)
![]() ;
;
3)
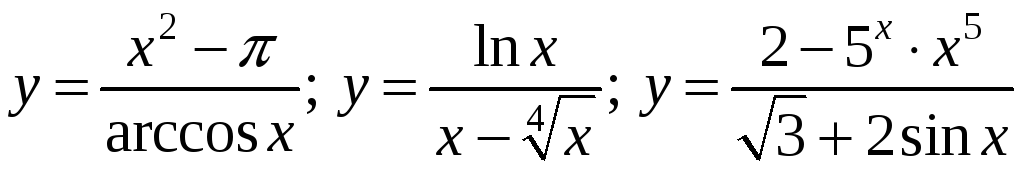 ;
;
4)
![]() ;
;
5)
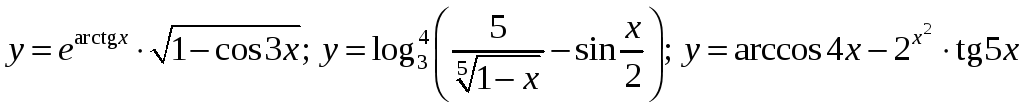 ;
;
6)
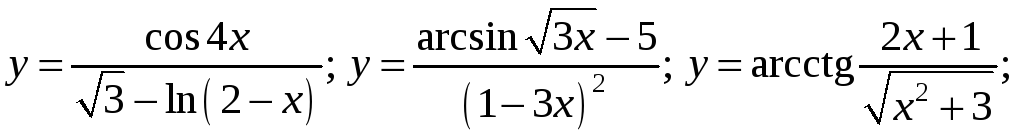
7)
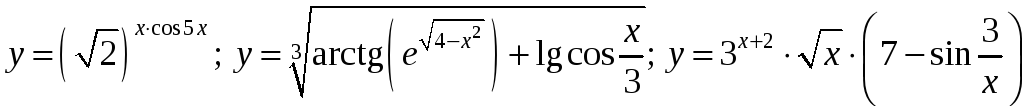 .
.
Завдання
4.9
Записати рівняння дотичної та нормалі
до графіка функції
![]() в точці з абсцисою
в точці з абсцисою
![]() .
.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
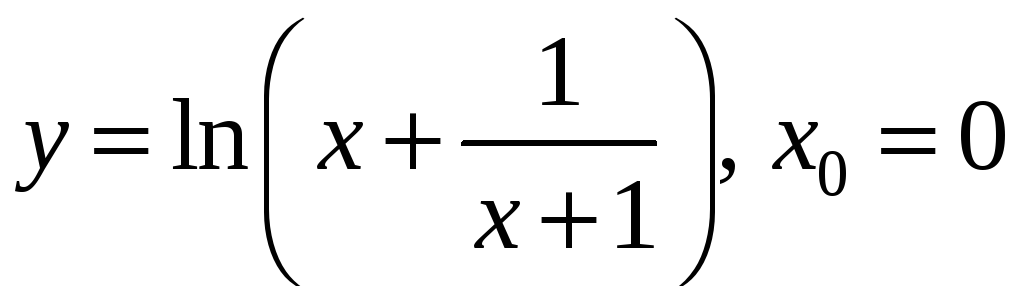
4)
![]() ;
5)
;
5)
![]() .
.
Завдання
4.10
Записати рівняння дотичної та нормалі
до кривої, що задана параметричними
рівняннями, у точці, де
![]() .
.
1)
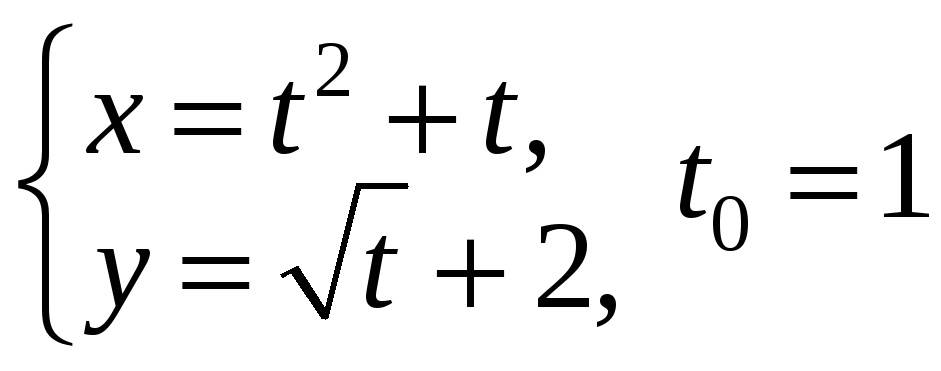 ;
2)
;
2)
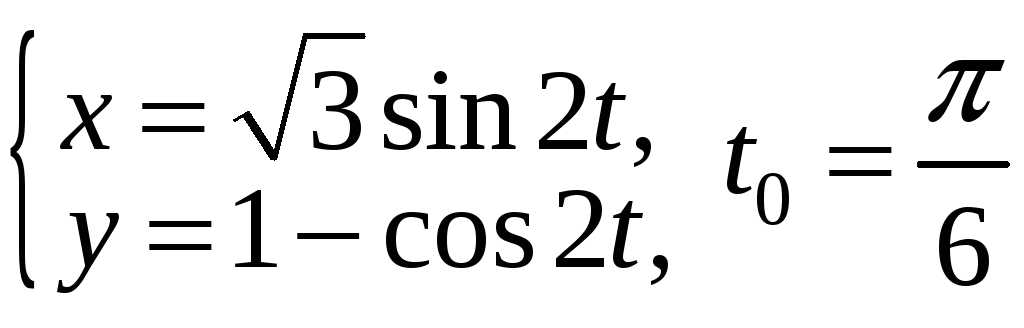 ;
3)
;
3) .
.
Завдання 4.11 Обчислити границі за допомогою правила Лопіталя.
1)
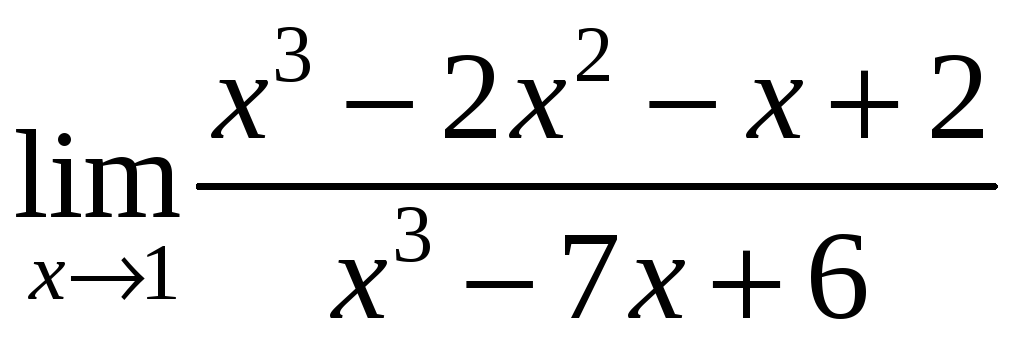 ;
2)
;
2)
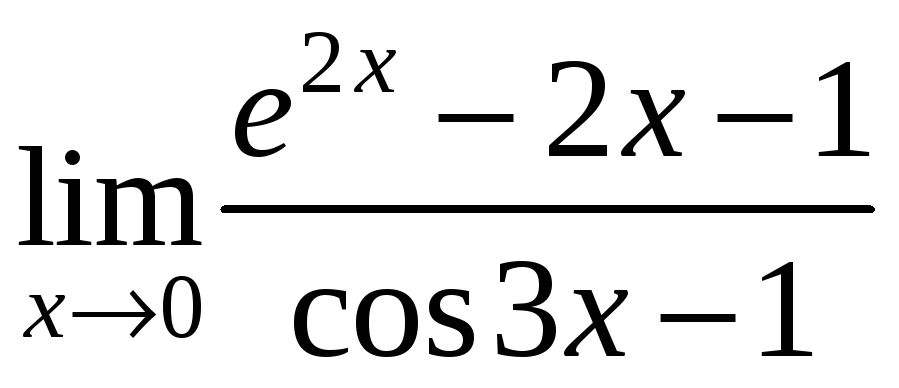 ;
3)
;
3)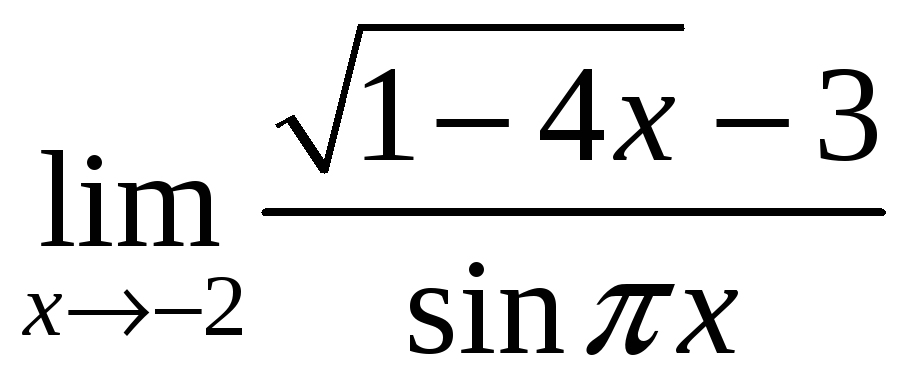 ;
4)
;
4)![]() ;
;
5)
 ;
6)
;
6)
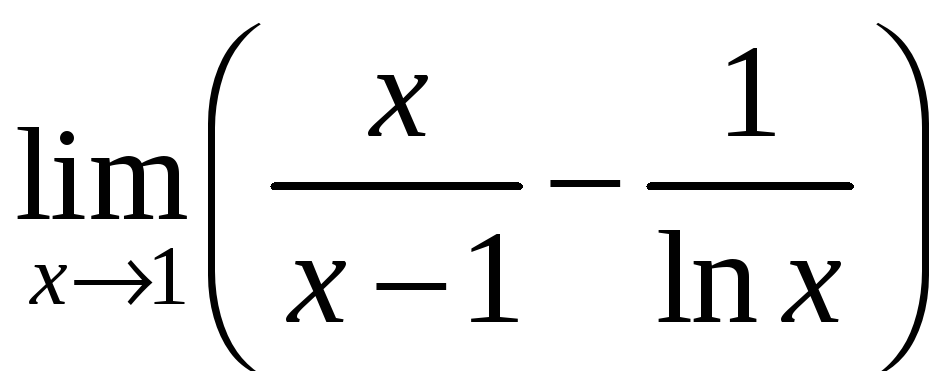 ;
7)
;
7)
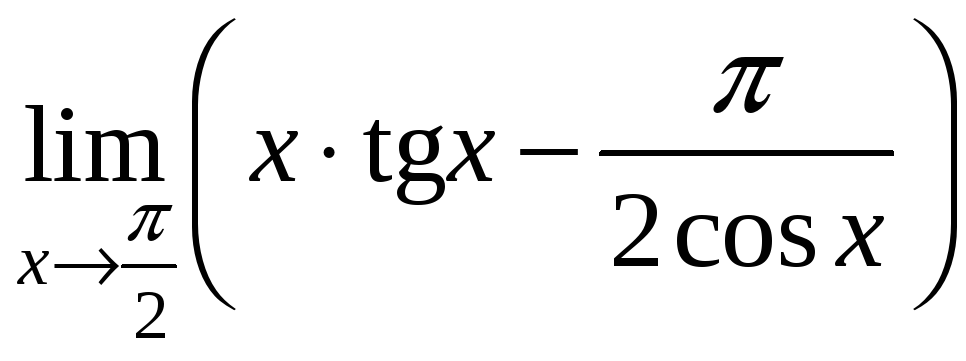 ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
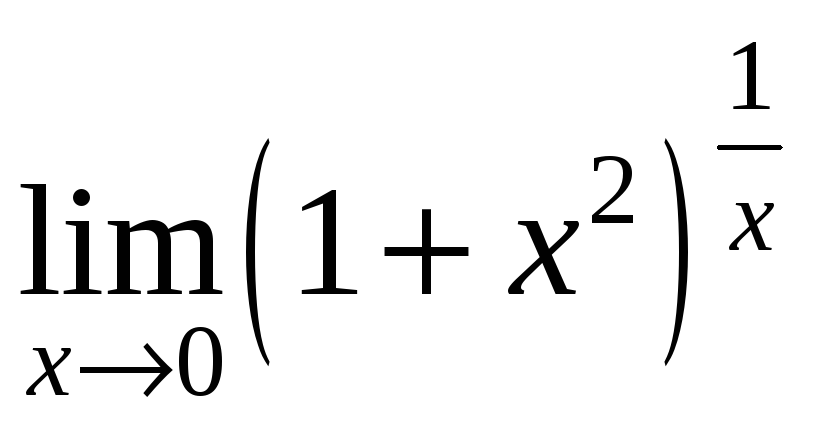 ;
11)
;
11)
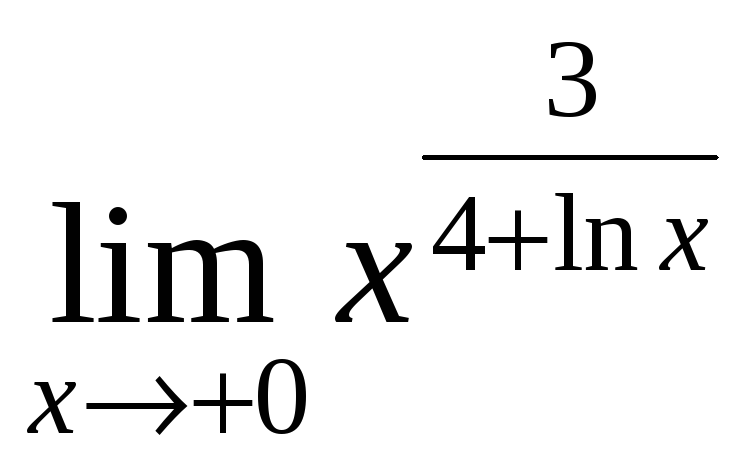 ;
12)
;
12)
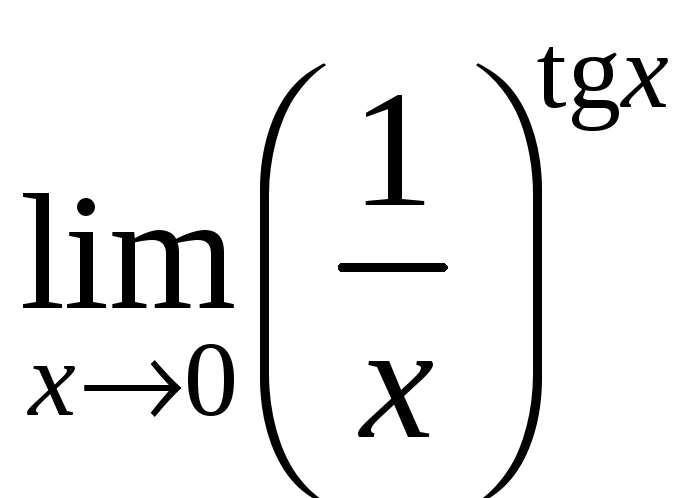 .
.
Завдання
4.12
Знайти похідні другого порядку
![]() .
.
1)
![]() ;
;
2)
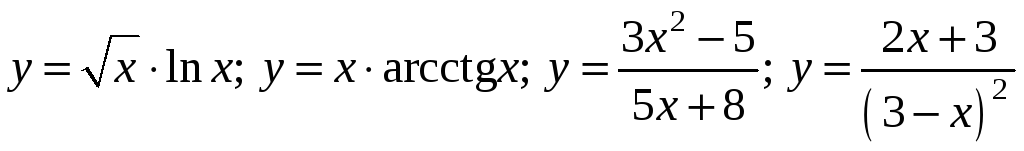 ;
;
3)
![]() ;
;
4)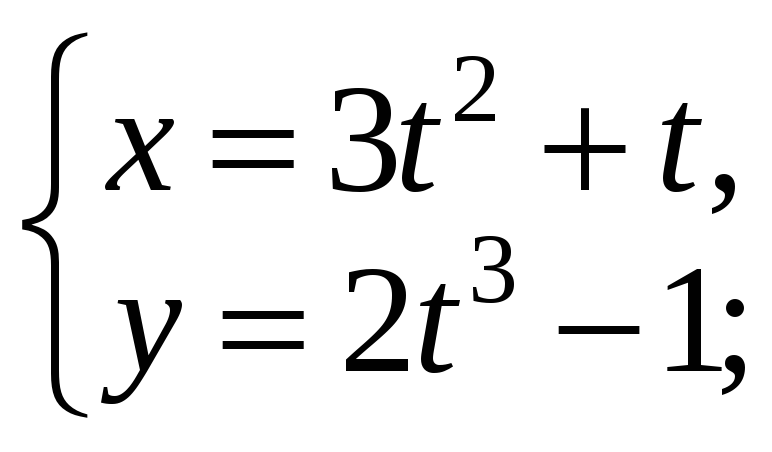 5)
5)
![]() 6)
6)
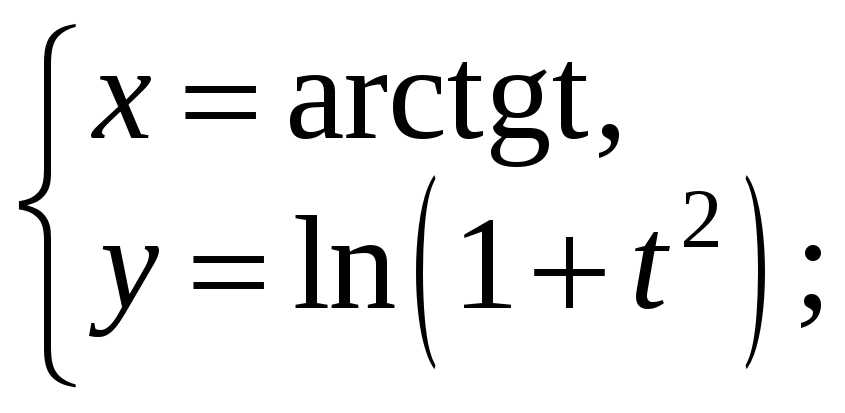 7)
7)
![]() 8)
8)
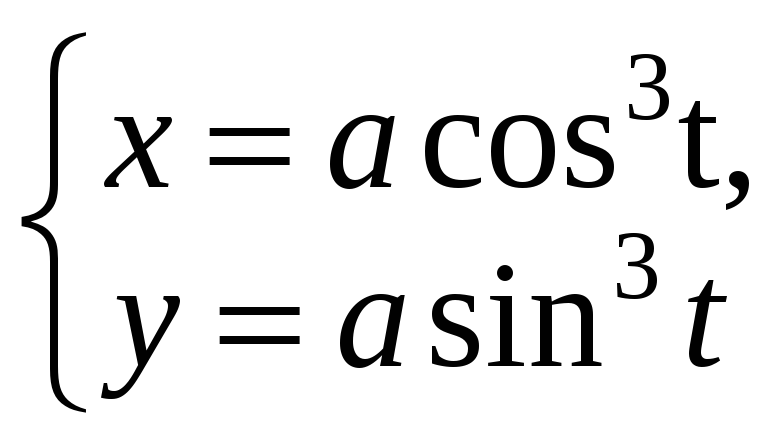 .
.
