§5 Рівняння поверхні і лінії у просторі

Рівняння виду називається рівнянням поверхні у прямокутній декартовій системі координат, якщо координати будь-якої точки , що належить поверхні, задовольняють це рівняння, а точки, що не належить їй - не задовольняють. Якщо рівняння поверхні має вигляд (- многочлен степеня ), то її називають алгебраїчною поверхнею порядку .

Будь-яку лінію у просторі можна розглядати як множину точок перетину двох поверхонь. Тому лінія визначається системою, що складається з рівнянь цих поверхонь

§6 Різні види рівняння площини у просторі

1.Площина –це алгебраїчна поверхня першого порядку, рівняння якої має вигляд

. (3.15)

Рівняння (3.15) називають загальним рівнянням площини.

2.По аналогії з виведенням рівняння (3.2) можна отримати рівняння площини, що проходить через точку перпендикулярно векторові ( його називають нормальним вектором площини)

. (3.16)

3. Рівняння площини, яка проходить через 3 задані точки , , можна отримати, використовуючи умову компланарності векторів (тут - довільна точка, що належить площині)

. (3.17)

4. Аналогічно до виведення рівняння (3.8) можна отримати рівняння площини, яка проходить через точки , , . Воно має вигляд

(3.18)

і називається рівнянням площини «у відрізках».

§7 Різні форми рівняння прямої у просторі

1. Загальні рівняння задають пряму як лінію перетину двох площин

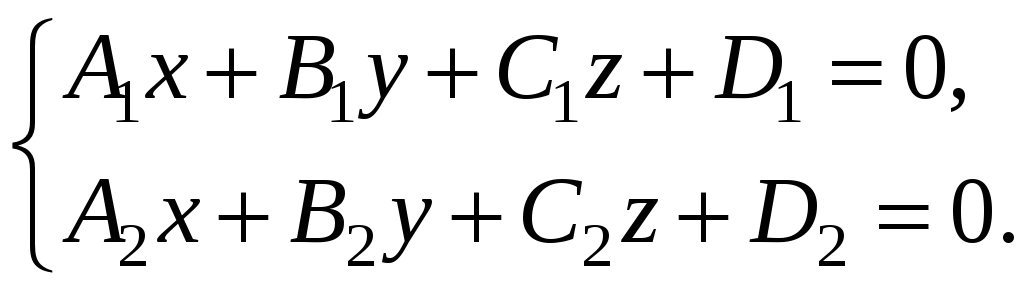(3.19)

2. Канонічні рівняння – це рівняння прямої, що проходить через точку паралельно векторові ( його називають напрямним вектором прямої)

. (3.20)

Вивести рівняння (3.20) можна по аналогії з рівнянням (3.3).

3. Якщо в рівняннях (3.20) позначити через коефіцієнт пропорційності, що дорівнює кожному з відношень, то вони будуть еквівалентні трьом рівнянням

, (3.21)

які називаються параметричними рівняннями прямої.

4. З рівнянь (3.20) випливає, що рівняння прямої, яка проходить через дві задані точки , , має вигляд

. (3.22)

§8 Кут між двома площинами

Один з лінійних кутів між площинами та дорівнює куту між їх нормальними векторами та . Тому .

Умови паралельності і перпендикулярності площин:

а) ,

б) .

§9 Кут між двома прямими

Кут між двома прямими 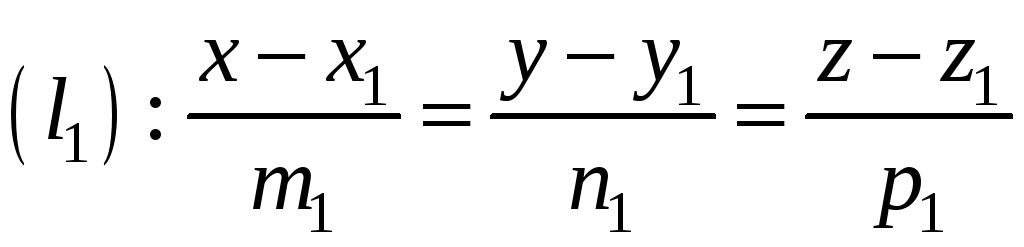та визначається як кут між їх напрямними векторами та . Він обчислюється за формулою

Умовою паралельності прямих є колінеарність їх напрямних векторів

.

Умовою перпендикулярності прямих є ортогональність їх напрямних векторів

.

§10 Кут між прямою та площиною. Умови паралельності і перпендикулярності

Оскільки кут між прямою з напрямним вектором і площиною з нормальним вектором в залежності від напряму цих векторів може визначатися однією з двох рівностей: або , то

.

Умовою паралельності прямої і площини є ортогональність напрямного вектора прямої і нормального вектора площини

.

Умовою перпендикулярності прямої і площини є колінеарність напрямного вектора прямої і нормального вектора площини

.