§2 Кут між двома прямими. Ознаки паралельності і перпендикулярності прямих

Один з кутів, що утворюються між двома прямими та дорівнює куту між їх нормальними векторами і . Отже

Отже ;

Умова паралельності прямих: .

Умова перпендикулярності прямих:

.

Якщо прямі задано рівняннями з кутовим коефіцієнтами і , то кут між ними можна обчислити за формулою

,

- найменший кут, на який треба повернути проти годинникової стрілки пряму, щоб вона співпала з прямою (рис.3.5). Доведення цієї формули безпосередньо випливає з геометричного змісту кутових коефіцієнтів і а також того факту, що .

Умови паралельності і перпендикулярності прямих

а) ;

б) .

§3 Відстань від точки до прямої

Обчислимо відстань від точки до прямої (рис. 3.6). Візьмемо на прямій будь-яку точку .

Зауважимо, що . Оскільки , отримаємо

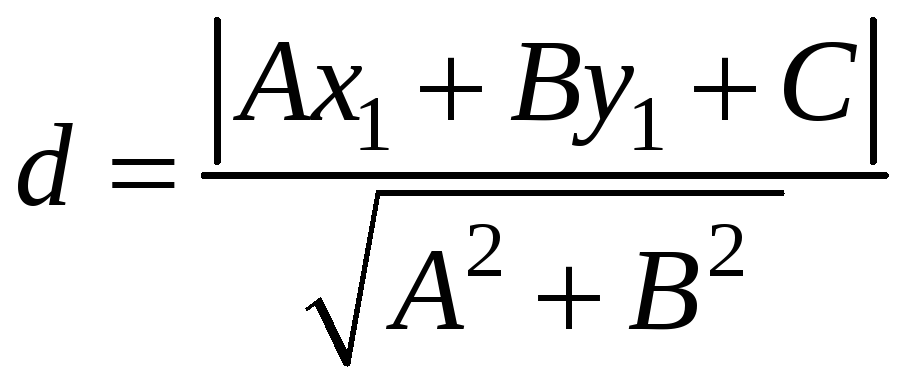. (3.9)

§4Лінії другого порядку

1.Еліпсом називається геометричне місце точок площини, для яких сума відстаней до двох фіксованих точок та цієї площини (що називаються фокусами) є величина стала (вона позначається ). Ця величина більша, ніж відстань між фокусами . Отже .

Якщо осі прямокутної декартової системи координат вибрано так, що фокуси еліпса знаходяться на осі і симетричні відносно початку координат, то , . Тоді для будь-якої точки еліпса маємо . Це означає, що . Піднесемо обидві частини останньої рівності до квадрату і зведемо подібні. Маємо . Якщо знову піднести обидві частини до квадрату, то можна отримати рівняння

, (3.10)

де . Рівняння (3.10) називають канонічним рівнянням еліпса.

Розглянемо еліпс, зображений на рис.3.7. Точки називають вершинами, - центром еліпса. та відповідно великою і малою півосями. Нехай - довільна точка еліпса. Відрізки та називають фокальними радіусами. Число , називають ексцентриситетом. Якщо (або ), то фокуси співпадають один з одним та з центром. Такий еліпс є колом радіуса . Прямі та називають директрисами еліпса.

2. Гіперболою називається геометричне місце точок, для яких різниця відстаней до двох фіксованих точок та площини (що називаються фокусами) є величина стала (вона дорівнює ). Якщо , то . Якщо осі прямокутної декартової системи координат вибрано так, що фокуси гіперболи знаходяться на осі і симетричні відносно початку координат, то по аналогії з тим, як виведено канонічне рівняння еліпса, можна отримати канонічне рівняння гіперболи. Воно має вигляд

, (3.11)

де . Рівняння (3.11) називають канонічним рівнянням гіперболи.

Розглянемо гіперболу, зображену на рис.3.8. Точки називають вершинами, - центром гіперболи. та відповідно дійсною та уявною півосями. Якщо - довільна точка гіперболи, то відрізки та називають її фокальними радіусами. Число , де - відстань від центру гіперболи до її вершини, називають ексцентриситетом , а прямі та - директрисами. Прямі та називають асимптотами гіперболи.

Зауважимо, що гіпербола може також задаватись канонічним рівнянням

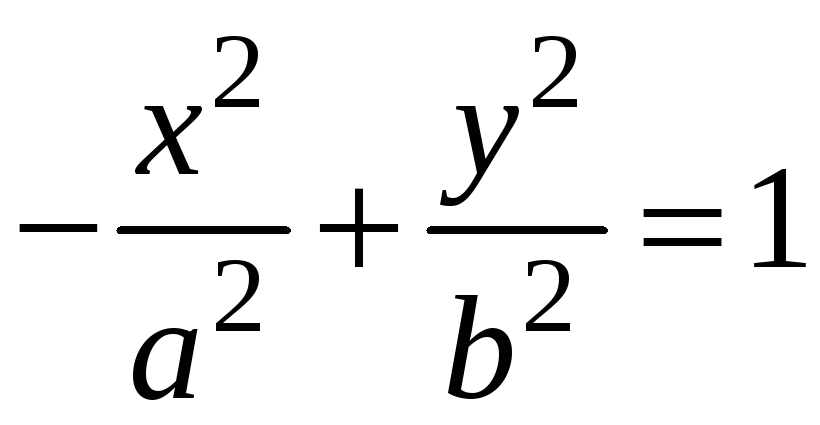. (3.12)

Фокуси і вершини такої гіперболи знаходяться на осі і симетричні відносно початку координат. Різниця відстаней від будь-якої точки гіперболи до її фокусів дорівнює .

3.Параболою називається геометричне місце точок, кожна з яких рівновіддалена від фіксованої точки (що називається фокусом) і деякої фіксованої прямої (директриси).

Введемо прямокутну декартову систему координат так, щоб вісь абсцис проходила через фокус параболи перпендикулярно до директриси. Спрямуємо її від директриси до фокуса, а початок координат розмістимо посередині між фокусом та директрисою (рис 3.9).

Можна довести, що в такій системі координат рівняння параболи має вигляд

, (3.13)

де . Рівняння (3.13) називається канонічним рівнянням параболи. Фокусом такої параболи є точка , а директрисою - пряма . Парабола в цьому випадку лежить в правій півплощині відносно осі і має одну вісь симетрії . Її називають віссю параболи. З нею парабола перетинається в одній точці , яку називають вершиною параболи.

Якщо вершина параболи знаходиться у початку координат, віссю симетрії є вісь абсцис, але парабола розміщена в лівій півплощині відносно осі , то вона задається рівнянням . Якщо вісь параболи суміщена з віссю ординат, а вершина - з початком координат, то рівняння параболи має вигляд

. (3.14)

Далі пропонуємо студентам самостійно розглянути питання про полярну систему координат на площині та рівняння ліній у полярній системі координат. Для цього рекомендуємо скористатися такими підручниками та навчальними посібниками: , .