Властивості лінійних операцій над векторами

1. Переставна властивість .

2. Сполучна властивість .

3. Розподільна властивість множення вектора на суму скалярів та скаляра на суму векторів або .

§ 3. Проекція вектора на вісь

Віссю будемо називати будь-яку пряму, що має напрям. Проекцією точки на вісь назвемо основу перпендикуляра, який опущено з точки на цю вісь.

Нехай задано вектор та вісь ( рис. 2.5), і - проекції точок і на . Зобразимо також вектор .

Проекцією вектора на вісь називається число, яке дорівнює довжині відрізка , якщо напрями вектора та осі співпадають, і протилежне до число в тому випадку, коли напрями протилежні. Позначають . Кут між вектором та віссю визначають як найменший з кутів, на який треба повернути вісь, щоб її напрям співпав з напрямом вектора .

Теорема 2.1. Проекція вектора на вісь дорівнює добуткові довжини вектора та косинуса кута між вектором та віссю.

Теорема 2.2. При множенні вектора на число його проекція також множиться на це число.

Теорема 2.3. Проекція суми векторів на вісь дорівнює сумі їх проекцій на цю вісь.

§ 4. Лінійна незалежність

Множина будь-яких елементів називається лінійним, або векторним простором, якщо вона задовольняє такі умови:

1) для довільних двох елементів існує третій елемент , який називається їх сумою, причому

1. ,

2. ,

3. в існує такий елемент , що 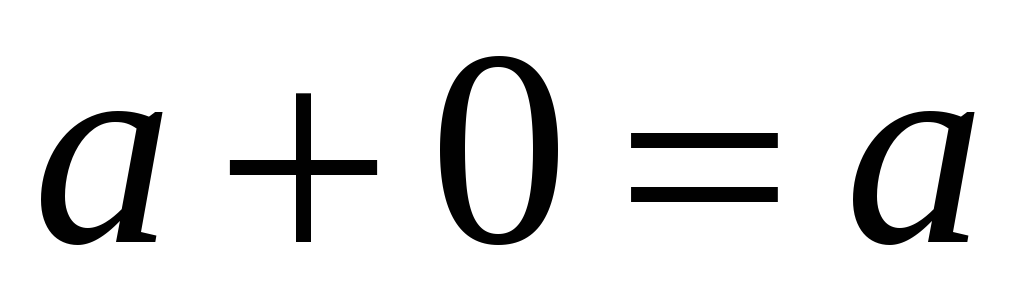для всіх ,

4. для кожного існує такий елемент , що ;

2) для довільного числа і довільного елемента визначений елемент (добуток елемента на число), причому

1. ,

2. ,

3. ,

4. .

Приклади лінійних просторів: множина дійсних чисел , множина векторів у просторі чи на площині, множина неперервних на деякому відрізку функцій.

Лінійною комбінацією елементів лінійного простору з коефіцієнтами називається сума .

Елементи називаються лінійно залежними, якщо існують такі числа , серед яких обов’язково є відмінні від нуля , що лінійна комбінація цих елементів з коефіцієнтами дорівнює нульовому елементу . Якщо остання рівність має місце тільки за умови: , то елементи називають лінійно незалежними.

Використовуючи ці означення неважко довести наступні твердження.

Теорема 2.4. Якщо хоча б один з елементів нульовий, то ця система елементів лінійно залежна.

Теорема 2.5. Якщо до системи лінійно залежних елементів приєднати ще один елемент, то отримана система є лінійно залежною.

Теорема 2.6. Елементи лінійно залежні тоді і тільки тоді, коли хоча б один з них можна подати у вигляді лінійної комбінації інших.

Розглянемо множину векторів у просторі.

Теорема 2.7. Необхідною і достатньою умовою лінійної залежності двох векторів є їх колінеарність.

Теорема 2.8. Необхідною і достатньою умовою лінійної залежності трьох векторів є їх компланарність.

Зауваження 1. З теореми 2.8 випливає твердження: для будь-яких двох не колінеарних векторів і будь-якого вектора , що лежить в одній площині з ними, знайдуться такі числа і , що виконано рівність:.

Теорема 2.9. Будь-які чотири вектори лінійно залежні.

Зауваження 2. Для будь-яких трьох не компланарних векторів і будь-якого вектора знайдуться такі три числа , що справедлива рівність: .