§3. Системи лінійних алгебраїчних рівнянь. Метод Крамера

Розглянемо систему лінійних рівнянь з невідомими

. (1.8)

Розв’язком системи (1.8) назвемо таку сукупність значень невідомих , , яка при підстановці в рівняння системи перетворює всі рівняння на тотожності. Систему, яка має розв’язок, назвемо сумісною, в протилежному випадку – несумісною. Систему, яка має єдиний розв’язок, назвемо визначеною, більше одного розв’язку – невизначеною.

Визначник називається головним визначником системи. Розглянемо визначники

, ,

тобто визначник утворюється із головного визначника системи шляхом заміни коефіцієнтів при - тому невідомому стовпцем з вільних членів системи.

Теорема 1.2. (теорема Крамера). Якщо визначник системи (1.8) не дорівнює нулю, то система має єдиний розв’язок (є визначеною). Розв’язок системи обчислюємо за формулами:

. (1.9)

Приклад. Розв’язати методом Крамера систему лінійних рівнянь

.

Розв’язання. Визначник системи . Тому система має єдиний розв’язок. Знаходимо

, , . За формулами (1.9) маємо , , .

§4. Метод Гаусса виключення невідомих

Формули Крамера мають велике теоретичне значення, але практичне їх застосування дуже обмежене, бо вони приводять до дуже громіздких обчислень. Частіше для розв’язування систем лінійних рівнянь застосовують метод виключення невідомих, що ґрунтується на так званих елементарних перетвореннях систем. Елементарними перетвореннями системи лінійних рівнянь вважаємо: 1) перестановку рівнянь; 2) множення обох частин рівняння на одне й те саме число, що не дорівнює нулю; 3) додавання до обох частин одного рівняння відповідних частин іншого рівняння, помножених на довільне число.

Метод Гаусса виключення невідомих полягає в тому, що за допомогою елементарних перетворень система зводиться до тотожньої їй системи, але простішого виду, з якої розв’язки системи можна легко знайти. Наприклад, система (1.8) при за допомогою елементарних перетворень завжди може бути приведена до так званого трикутного виду:

.

З цієї системи послідовно, починаючи з останнього рівняння, знаходять невідомі .

Приклад. Розв’язати методом Гаусса систему лінійних рівнянь

.

Розв’язання. За допомогою елементарних перетворень зведемо систему до верхнього трикутного виду.

Переставимо перше і трете рівняння. Додаємо до другого та третього рівняння перше, помножене відповідно на та на . Отримуємо або рівносильну їй систему 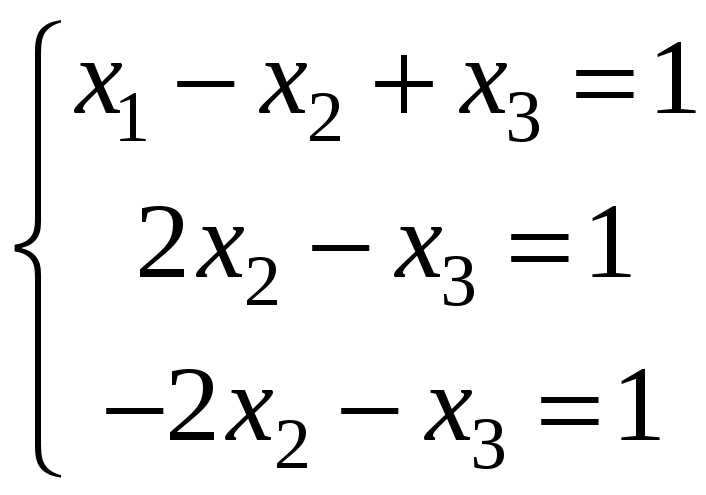. Додаємо друге та трете рівняння: . З добутої системи послідовно (знизу вгору) знаходимо: , , .

Зазначимо, що метод Гаусса можна використовувати для дослідження системи на сумісність, а також для розв’язування системи лінійних рівнянь з невідомими .

Приклад. Дослідити на сумісність систему лінійних рівнянь

.

Розв’язання. Виконуючи елементарні перетворення, отримуємо

, , . З останнього рівняння випливає несумісність системи.

Якщо шляхом елементарних перетворень систему (1.8) приведено до вигляду , то вона сумісна і невизначена. З останнього рівняння маємо . Надаючи невідомим довільних значень отримаємо трикутну систему рівнянь, з якої послідовно знайдемо . Таким чином нескінченну кількість розв’язків системи буде знайдено.

Приклад. Розв’язати систему лінійних рівнянь .

Розв’язання. Виконуючи елементарні перетворення, одержимо

, . Звідси

- довільне дійсне число.

Через неможливість докладного вивчення в рамках цього курсу лекцій питання про ранг матриці та сумісність системи, а також таких питань, як дії над матрицями, обернена матриця та матричного способу розв’язування лінійних систем, рекомендуємо студентам скористатися підручниками, задачниками та навчальними посібниками , , ,.