§7 Односторонні границі

Число назвемо лівосторонньою границею функції в точці , якщо для будь-якої додатної сталої , знайдеться така , що для всіх з інтервалу виконано нерівність . Пишуть або . Аналогічно формулюється означення правосторонньої границі функції в точці , тільки нерівність має виконуватись для будь – якого з інтервалу . Пишуть або . Наприклад .

Теорема 4.4 Функція має границю в точці , якщо вона має в цій точці лівосторонню і правосторонню границі і

.

Дамо означення границь функції на і . Визначимо їх формулами 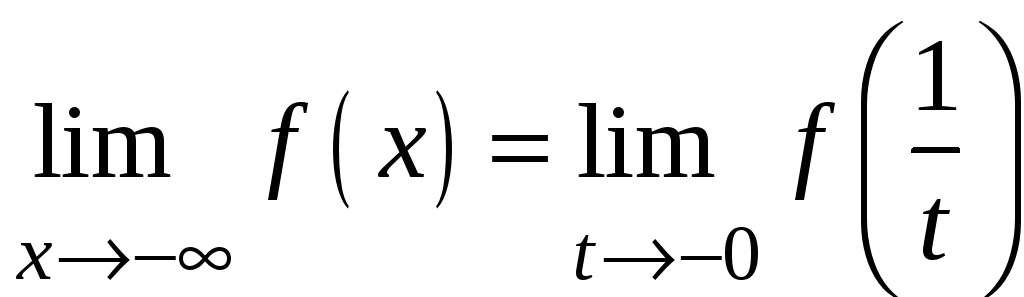і .

§8 Точки розриву функції

Якщо функція не є неперервною в точці , то її називають розривною в цій точці, а називають точкою розриву. Якщо - точка розриву функції , то, враховуючи теорему 4.4 в цій точці має порушуватись хоча б одна з умов:

1. існують скінченні односторонні границі і ;

2. вони співпадають, тобто;

3. односторонні границі дорівнюють значенню функції в точці

, тобто .

Якщо в точці розриву виконується умова 1, то цю точку називають точкою розриву першого роду. Якщо порушується тільки умова 3, то називають точкою усувного розриву. Якщо порушується умова 1, тобто, хоча б одна з односторонніх границь в точці не існує або дорівнює , то називають точкою розриву другого роду.

§9 Похідна

Нехай функція визначена в точці і деякому її околі . Дамо аргументові приросту так, щоб . Знайдемо приріст функції . Якщо границя відношення приросту функції до приросту аргументу коли існує і дорівнює скінченому числу, то це число називають похідною функції в точці . Пишуть .

З геометричної точки зору похідна дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою (рис. 4.1).

Розкриємо механічний зміст похідної. Якщо точка рухається по прямій, яка суміщена з віссю , при цьому залежність її координати від часу визначається функцією , то похідна дорівнює миттєвій швидкості точки в момент часу , тобто . Похідна від функції швидкості в точці дорівнює прискоренню точки в цей момент часу .

Таблиця похідних

Правила обчислення похідних

Якщо кожна з функцій і має похідну в точці , то в цій точці

1. існує похідна від суми цих функцій і вона дорівнює сумі похідних, тобто ;

2. сталий множник можна винести за знак похідної, тобто ;

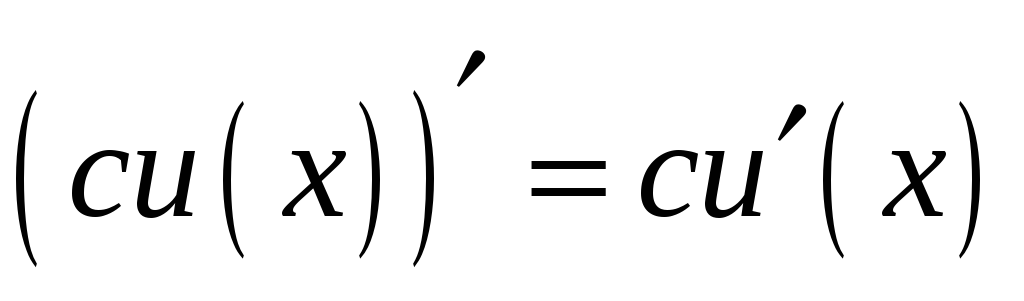3. існує похідна від добутку і вона обчислюється за формулою ;

4. існує похідна від частки і вона обчислюється за формулою , якщо .

Теорема 4.5. Якщо функція має похідну в точці , то вона неперервна в цій точці.

Доведення. Надамо аргументу в точці приросту . Тоді функція отримає відповідний приріст , при цьому 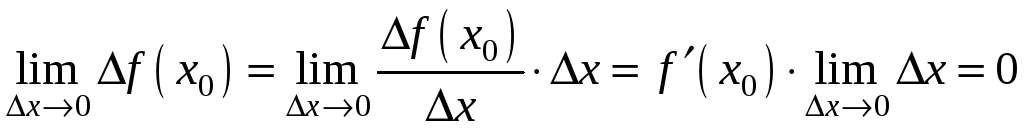, що і означає неперервність функції в даній точці.

Теорема 4.6 (про похідну складеної функції). Якщо функція має похідну в точці , а функція має похідну у відповідній точці , то складена функція має похідну в точці , і похідна обчислюється за формулою .

Доведення. Надамо аргументу в точці приросту . Тоді змінні і отримають відповідні прирости і . Маємо

.

Тут ми скористалися теоремою 4.5. Функція неперервна в точці , оскільки має похідну в цій точці. Отже, якщо , то і .

Приклад. Знайти похідну .

Розв’язання. За теоремою 4.6 маємо

.

Розглянемо функцію, наприклад . Знайдемо її похідну . Похідна також є функцією аргументу , знайдемо тепер її похідну. Маємо . Похідну від похідної функції назвемо її похідною другого порядку. Пишуть . Аналогічно можна визначити похідну третього і більш високих порядків.