§ 6. Частинні похідні другого порядку.

Розглянемо функцію двох змінних . Для приклада візьмемо . Знайдемо частинні похідні. Маємо і . Ці частинні похідні (їх називають частинними похідними першого порядку) є функціями від та . Частинні похідні від них називаються частинними похідними другого порядку і визначаються формулами

.

Для вказаної функції отримаємо

.

Частинні похідні другого порядку можна позначати так

.

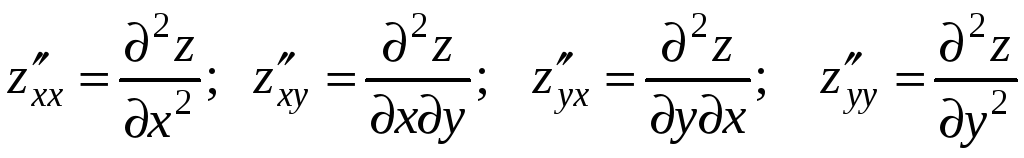Теорема 5.7 Якщо функція і її частинні похідні , і неперервні в точці і деякому її околі, то в цій точці .

Частинні похідні третього порядку визначають за формулами:

;

.

§ 7. Екстремум функції двох змінних

Точка називається точкою максимуму (мінімуму) функції , якщо існує такий окіл точки , що для будь-якої точки з цього околу, крім самої точки , виконується нерівність ( для точки мінімуму).

Точки максимуму і мінімуму називаються точками екстремуму.

Теорема 5.8 (необхідна умова екстремуму).

Якщо функція досягає екстремуму в точці ,то кожна з її частинних похідних першого порядку дорівнює нулю або не існує.

Точки, в яких (або не існує) і (або не існує),називаються критичними точками функції .

Теорема 5.9 (достатня умова екстремуму).

Нехай 1) в деякій області, що містить точку функція має неперервні частинні похідні до третього порядку включно;

2) точка є критичною точкою функції .

Тоді, якщо , то в точці функція має екстремум. При цьому, якщо , то - точка мінімуму, якщо , то - точка максимуму.

Приклад. Дослідити на екстремум функцію .

Розв’язання. Знайдемо частинні похідні. Маємо

.

Прирівняємо і до нуля, тобто складемо систему рівнянь . Розв’язавши її одержимо критичні точки , .

Знайдемо частинні похідні другого порядку. Маємо

. Тоді . , отже - точка екстремуму. Оскільки , то - точка мінімуму і .

не є точкою екстремуму, оскільки .

§ 8. Умовний екстремум

Іноді доводиться розв’язувати задачу знаходження екстремумів функції двох змінних , і ці змінні не є незалежними. Вони пов’язані одна з одною якоюсь додатковою умовою, наприклад, рівнянням

. (5.5)

Якщо рівняння (5.5) розв’язується відносно однієї з змінних, наприклад, відносно : , то підставимо замість в функцію . Вона перетворюється на функцію однієї змінної , яку слід дослідити на екстремум (розділ 4, §12). Якщо ж рівняння (5.5) неможливо розв’язати відносно та відносно , то для розв’язання задачі умовного екстремуму використовують метод множників Лагранжа. З цим методом можна ознайомитись в .

§ 9. Найбільше і найменше значення функції двох змінних в замкненій обмеженій області

Як стверджує теорема 5.1, неперервна в замкненій обмеженій області функція досягає в ній свого найбільшого і найменшого значень. Якщо свого найбільшого або найменшого значення функція досягає у внутрішній точці області , то ця точка обов’язково є критичною. Тому вказану задачу можна розв’язати за такою схемою:

1) знайти критичні точки функції , що належать області і обчислити значення функції в них;

2) розв’язати задачу умовного екстремуму функції на границі області;

3) серед усіх знайдених в пунктах 1 і 2 значень функції обрати найбільше і найменше.

Приклад. Для функції знайти найбільше і найменше значення функції в області , обмеженій лініями , .

Розв’язання. Побудуємо задану область – трикутник .

Знайдемо частинні похідні. Маємо . Прирівняємо і до нуля, тобто . Розв’язавши цю систему, одержимо критичну точку , яка належить області . Знайдемо .

Задамо відрізок границі області умовами: . Досліджувана функція на цьому відрізку перетворюється на функцію однієї змінної , яка є спадною при (адже її похідна від’ємна на цьому проміжку). Отже свого найбільшого значення на даному відрізку вона досягає при , а найменшого – при . Знайдемо їх , . Розглянемо тепер відрізок :. Отримаємо функцію , похідна якої дорівнює нулю при . Оскільки критична точка , то знайдемо , знайдемо також . Зауважимо, що вже знайдено. Для відрізка , який задається умовами отримаємо функцію . Нулем її похідної є точка , що належить відрізку . Ординату відповідної точки відрізка знайдемо з рівності . Маємо . Обчислимо , значення і ми вже знаходили. Таким чином, функція свого найбільшого в заданій області значення досягає в точці . Найменше значення досягається функцією в точці .

Для більш глибокого вивчення функцій кількох змінних рекомендуємо скористатися підручниками та навчальними посібниками , , ,.