§10 Диференціал функції

Функція називається диференційовною в точці , якщо її приріст в цій точці може бути представлений у вигляді , де - нескінченно мала при . Зауважимо, що і залежать від точки .

Теорема4.7. Якщо функція диференційовна в точці , то вона неперервна в цій точці.

Доведення є очевидним.

Теорема 4.8. Функція диференційовна в точці тоді і тільки тоді, коли вона має похідну в цій точці.

Доведення. Необхідність. Нехай диференційовна в точці , тоді . Отже, функція має похідну в точці , і ця похідна дорівнює .

Достатність. Нехай має похідну в точці : . Тоді . Отже, різниця 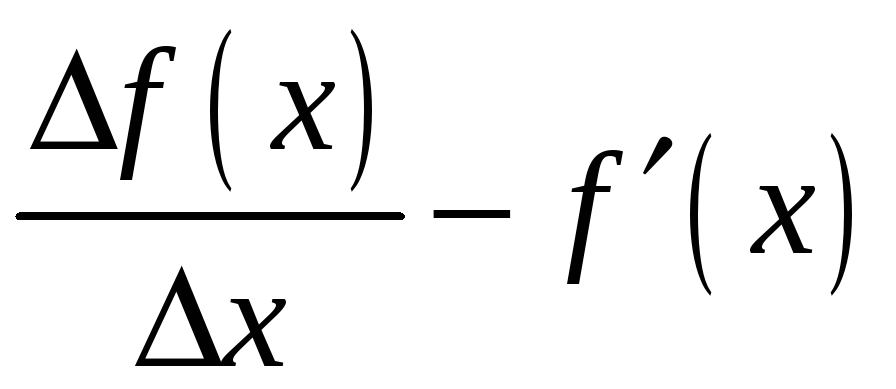- нескінченно мала при функція.

Позначимо її через . Тоді або

, (4.2)

що і означає диференційовність функції в точці . Теорему доведено.

Таким чином, диференційовність функції і існування похідної – це одне і теж поняття. Тому обчислення похідної називається також диференціюванням.

Розглянемо формулу (4.2). Головна, лінійна відносно приросту аргументу, частина приросту диференційовної функції називається диференціалом цієї функції. Пишуть

. (4.3)

Диференціалом незалежної змінної назвемо її приріст. Тобто . Як бачимо, таке означення не суперечить означенню диференціала функції, адже для функції маємо .

Замінивши у формулі (4.3) на , одержимо

. (4.4)

З формули (4.4) випливає рівність 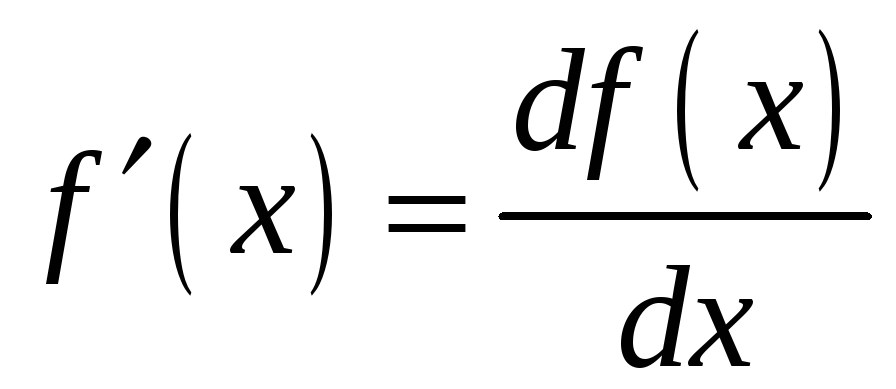. Таким чином, похідну можна розглядати як відношення диференціалу функції до диференціалу незалежної змінної.

Теорема 4.9 (про інваріантність форми диференціала). Якщо функція диференційовна в точці , а функція диференційовна у відповідній точці , то . Тобто форма диференціалу незалежна (інваріантна) від того, чим є аргумент - незалежною змінною, або диференційовною функцією.

Доведення з очевидністю випливає з теореми 4.6.

З формули (4.2) маємо (при малих значеннях ), тобто

(4.5)

Приклад. Обчислити наближено , замінивши приріст функції диференціалом.

Розв’язання. Застосуємо формулою (4.5) для функції при . Знайдемо похідну . Маємо . Тоді .

§11 Основні теореми про диференційовні функції

Теорема 4.10 (Ферма). Якщо функція диференційовна на інтервалі і в деякій точці досягає свого найбільшого або найменшого значення, то .

Теорема 4.11 (Ролля). Якщо функція неперервна на відрізку , диференційовна на інтервалі і , то на цьому інтервалі знайдеться така точка , що .

Зокрема, між двома нулями такої функції знаходиться нуль її похідної.

Теорема 4.12 (Лагранжа). Нехай функція неперервна на відрізку і диференційовна на інтервалі . Тоді на цьому інтервалі знайдеться точка , в якій справедлива рівність

. (4.6)

Геометрична інтерпретація теореми. Розділимо обидві частини рівності (4.6) на , отримаємо рівність

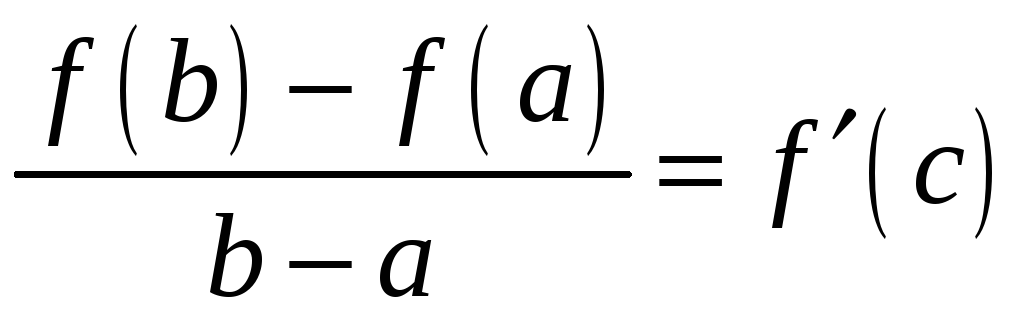(4.7)

Ліва частина рівності (4.7) дорівнює кутовому коефіцієнту січної до графіка функції , а права частина кутовому коефіцієнту дотичної до цього графіку в точці з абсцисою (рис. 4.2). Отже, якщо умови теореми Лагранжа виконані, то на інтервалі знайдеться така точка , що дотична до графіка функції в точці буде паралельна січній .